- 二叉树的定义:
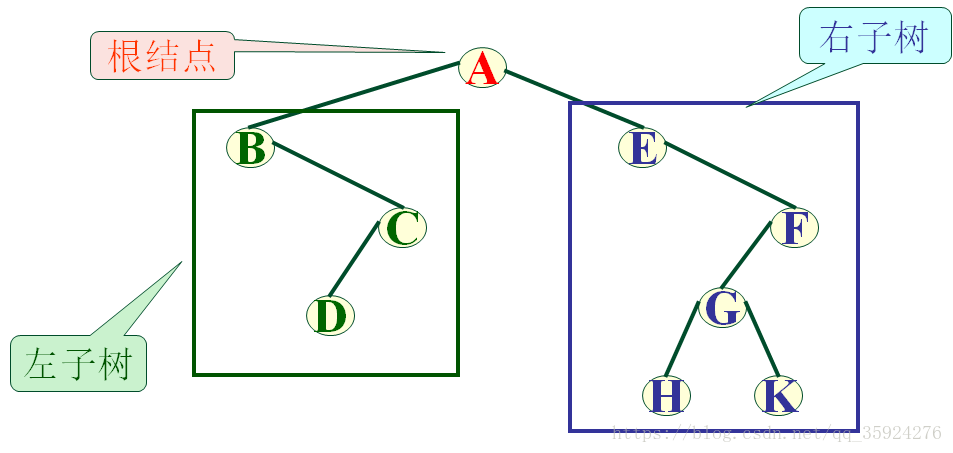
二叉树(Binary Tree)是n(n>=0)个结点的有限集合,该集合或者为空集(空二叉树),或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树的二叉树组成。
二叉树与树的区别:
二叉树不是树的特殊情形,而是与树不同的数据结构,即二叉树并不等价于2 度的树。
1)一个二叉树中可以不存在度为2的结点。(不是都需要两棵子树,而是最多可以是两棵,没有子树或者有一棵子树也都是可以的。)
2)二叉树中结点的子树有左、右之分,即使在只有一棵子树的情况下,也应分清是左子树还是右子树。
- 特殊的二叉树
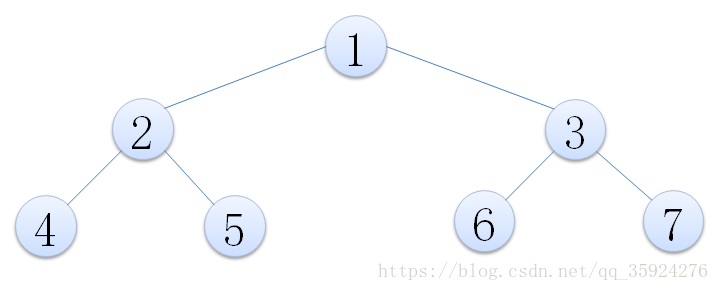
(一)满二叉树:在一棵二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子都在同一层上,这样的二叉树称为满二叉树。(深度为 k 且有2 k-1个结点的二叉树)
特点有:
–叶子只能出现在最下一层。
–非叶子结点的度一定是2。
–在同样深度的二叉树中,满二叉树的结点个数一定最多,同时叶子也是最多。
(二)完全二叉树:对一棵具有n个结点的二叉树按层序编号,如果编号为i(1<=i<=n)的结点与同样深度的满二叉树中编号为i的结点位置完全相同,则这棵二叉树称为完全二叉树。(近似满二叉树,树中所含的 n 个结点和满二叉树中编号为 1 至 n 的结点一一对应。)
特点有:
–叶子结点只能出现在最下两层。
–最下层的叶子一定集中在左部连续位置。
–倒数第二层,若有叶子结点,一定都在右部连续位置。
–如果结点度为1,则该结点只有左孩子。
–同样结点树的二叉树,完全二叉树的深度最小。
•注意:满二叉树一定是完全二叉树,但完全二叉树不一定是满二叉树。
(三)严格二叉树(正则二叉树):若二叉树中不存在度为1的结点,则称作严格二叉树。
- 二叉树的性质(可验证)
性质1——在二叉树的第 i 层上至多有 个结点 ( i≥1)。
性质2 :深度为 k 的二叉树至多有 个结点 ( k≥1)。
性质3 : 对于任何一棵二叉树,若它的叶子结点数为n0 ,2 度结点数为n2,则 。
–再假设度为1的结点数为n1,则二叉树T的结点总数n=n0+n1+n2
–其次我们发现连接数总是等于总结点数n-1,并且等于n1+2*n2
–所以n-1=n1+2*n2
–所以n0+n1+n2-1=n1+n2+n2
–最后n0=n2+1
性质4 :具有n 个结点的完全二叉树的深度为。
设完全二叉树的深度为 k 则根据性质2 和完全二叉树的定义有
即 ∵ k 是整数 ∴ k =
性质5:若对一棵有 n 个结点的完全二叉树自上而下先左后右进行从 1 至 n 的编号(即按层次次序编号),
则对完全二叉树中任意一个编号为 i 的结点, 有:
(1) 若 i=1,则该结点是二叉树的根,无双亲,否则,其双亲结点是编号为 的结点;
(2) 若 2i>n,则该结点无左孩子,否则,其左孩子结点是编号为 2i 的结点;
(3) 若 2i+1>n,则该结点无右孩子结点,否则,其右孩子结点是编号为2i+1 的结点。
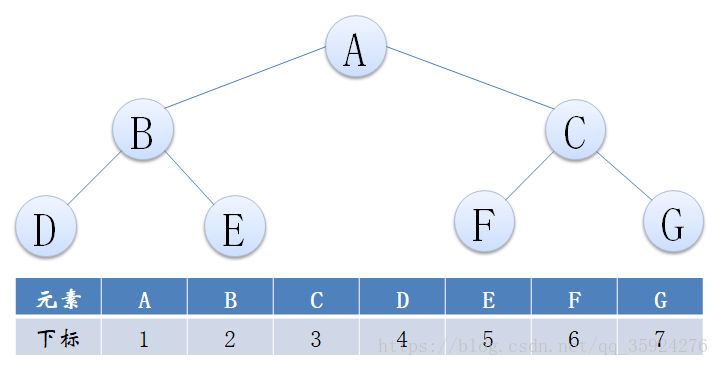
(一)二叉树的顺序存储结构:就是用一维数组存储二叉树中的各个结点,并且结点的存储位置能体现结点之间的逻辑关系。
完全二叉树优势如下(数组直接能表现出逻辑结构):
- 二叉树的存储结构:二叉树是一种特殊的树,由于它的特殊性,使得用顺序存储结构或链式存储结构都能够简单实现。
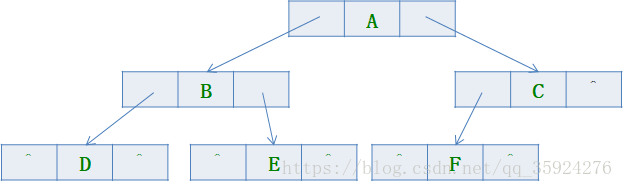
一般情况(不存在结点用^表示):
极端情况(造成极大浪费):
(二)二叉树的链式存储结构:
//二叉链表
typedef struct BiTNode
{
TElemType data;
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
//结构体类型,结构体指针类型