机器学习相关知识点面试总结

博主近日参加了导师实验室的面试，因为对机器学习比较感兴趣，所以简历上写了目前已实现SVM，Adaboost等算法，然后接下来的二十多分钟面试基本问SVM了。很多知识点其实以前也有遇到，只是没有详细总结，此处po主班门弄斧，不到位的地方还请大家指正。

1）朴素贝叶斯的平滑处理过程是什么？

这点其实在Andrew Ng的《Machine Learning》课程里面有讲，简单来说就是拉普拉斯平滑处理。即在最后分类的概率部分分母加上类别总数，分子加1，主要是为了防止新的单词在词集中从未出现的情况。详细原因可参考：

https://blog.csdn.net/qq_35083093/article/details/75340848

2）SVM与感知机的联系与区别？

先说联系：

①SVM与感知机本质上都是判别式模型，即直接学习P(y|x)

②感知机是SVM的基础，SVM不引入核函数的话和感知机一样都是线性分类器

再说区别：

①分类原理不一样。SVM的原理主要是几何间隔最大化，而且分类平面存在且唯一；感知机的思想是分类正确不调整权重，分类错误会对权重做进一步更新，这样造成的结果是每次分类完成后确定的分类平面不唯一。

②适用范围不一样，主要针对近似线性可分数据集和线性不可分数据集。对于SVM而言，最基本的是线性可分支持向量机，这只针对数据集完全线性可分时适用，当然感知机此时也适用；对于近似线性可分数据集，SVM对函数间隔引入松弛条件（软间隔最大化，直接表现就是在完全线性可分时的目标函数上加上惩罚项），而单层感知机对于这类数据集不能收敛，不能得到最后的分类平面；最后对于线性不可分数据集，SVM引入核函数，将线性不可分数据映射到高维，然后再采用线性可分时的思想来解决，然而单层感知机不能处理这类问题，典型的如异或问题。

③损失函数不一样。这部分与①有重叠，但还是想提出来说。我们知道二类分类的损失函数即为0-1损失，但他有个缺点就是不可导，没办法进一步进行优化。SVM的损失函数是hinge loss（合页损失），可以看做是对0-1损失的上界，对0-1损失函数不可导的一种优化；其次SVM的损失函数可看做是感知机损失函数（虚线部分）沿函数间隔轴向右平移一个单位的结果，这说明SVM对相对于感知机对分类间隔的要求更高。

3）SVM是个二分类算法，其本身是否可以由二分类问题转化为多分类问题，如果可以，请问怎么转？常见的由二分类到多分类问题的转化方法有哪些？

参考自：https://www.cnblogs.com/CheeseZH/p/5265959.html

问题一：SVM本身是可以直接转换为多分类的，即将多个分类面的参数整合到一个最优化问题中，但往往求解困难。

问题二：常见的二分类到多分类方法有one against one和one against all，具体分析可参考上述链接。

one against one采用一对一的方式，最后每轮两两比较的投票总数排序，决定所属的类别；one against all采用一对多的方式，最后直接比较所有轮的最大结果，决定目标所属分类。

各自缺点分析：

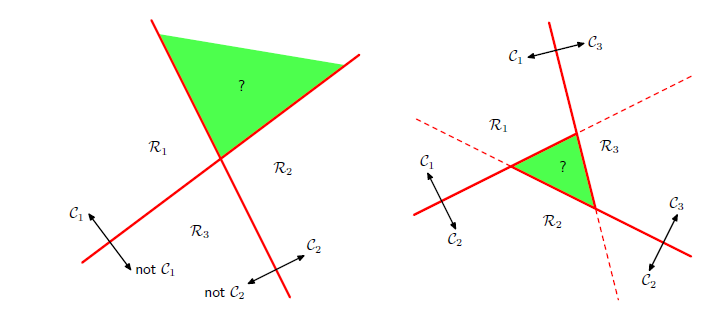
对于one against one而言，需要训练 $\frac{N*(N-1)}{2}$ 个分类器，代价相对较高；对于one against all而言，需训练N个分类器，但这种方法存在bias可能性（如下图，左侧为one against one，右侧为one against all，绿色部分为分类歧义区）

4）SVM与logistic回归的区别，其适用数据集大小范围各是哪些？

区别：

①损失函数。SVM是hinge loss，logistic regression是对数损失。

②离群点对分类平面的影响。SVM的分类平面只考虑支持向量部分，logistic regression的分类面会考虑所有点的影响。

③正则化。SVM目标函数自带正则化，logistic regression需要自己添加正则函数。

两者适用的数据集范围：

参考自Andrew Ng的《Machine Learning》

假设m是样本数，n是特征的数目：
1、如果n相对于m来说很大，则使用logistic回归或者不带核函数的SVM（线性分类）
2、如果n很小，m的数量适中（n=1-1000，m=10-10000），使用带核函数的SVM算法
3、如果n很小，m很大（n=1-1000,m=50000+）,增加更多的特征，然后使用logistic回归或者不带核函数的SVM。

5）Adaboost算法的误差上界？

Adaboost算法最终分类器的训练误差上界为：

$\frac{1}{N}\sum(I(G(x_{i})\neq y_{i}))))\leqslant \frac{1}{N}\sum exp\left ( -y_{i} f\left ( x_{i} \right )\right )$

此处给出简单的证明：

如果分类器分类正确，则左边式子为0，而右边 $y_{i}f\left ( x_{i} \right )\geq 0$ ，即 $\frac{1}{N}\sum exp\left ( -y_{i}f\left ( x_{i} \right ) \right )\geq 0$ ;

如果分类器分类错误，则左边式子为1，而右边 $y_{i}f\left ( x_{i} \right )< 0$ ，此时 $\frac{1}{N}\sum exp\left ( -y_{i}f\left ( x_{i} \right ) \right )\geq 1$ 。

故原等式成立。

参考自：

https://blog.csdn.net/luoshixian099/article/details/51073885

李航，《统计学习方法》

Andrew Ng，《Machine Learning》

机器学习相关知识点面试总结

猜你喜欢