算法设计与分析—基础知识

前言

      回顾我以往的博客，曾想畅游leetcode的题海，踏遍千山翻遍万水以求有所进步，刷题到不到一半便因为硕士开题而中道崩殂；曾想成为一名Qt高手，想把Qt的官方文档翻译成中文，却在浩如烟海的官方文档中迷失自己，仅仅有几篇孤零零的翻译文稿，翻译计划最终被我抛弃；曾想要将阅读的文献进行总归纳结，最后写成读书笔记，执行了几天之后因为写博客太过艰辛而逐渐的不了了之；曾经信誓旦旦要坚持学习英语，但是英语考试结束后这个计划早已被我抛之脑后，那些所谓的雄心壮志和豪言壮语，在我贪玩懒惰的本性中逐渐烟消云散。到头来，发现很多事情都是虎头蛇尾，从一而终的事情却寥寥无几。
    我想我最大的问题是想的太多，做的太少，想学的东西太多太多，但是真正去下定决心钻研努力少之又少，我的整个知识体系庞杂并且毫无章法。时至今日，我慢慢发现我不需要擅长很多东西，但是定下的学习目标就应该很好的完成它，我慢慢懂得了什么叫有始有终，凡是我们下定决心去做的事情，值得我们去做的事情，都应该有始有终。
     随着岁月的更迭，课本会变得破旧不堪，逐渐被我所遗弃，写下的学习却笔记一直在那里，岁月的长河奔流不息，纵使时过境迁，带不走的，却娟娟细流组成的知识海洋。

正文

     计算机算法在计算机专业中有这举足轻重的地位，无论是找工作的面试还是在程序设计中都离不开计算机算法设计，为了方便的对这些知识的进行复习回顾，在学习之余，特写下算法设计与分析的博客,这个小目标一定要坚持到底！

重要的数学概念和定义

• 渐进上界和渐进下界

设$f和g$是定义域为自然数集$N$上的函数.

(1) 若存在正数c和$n_0$使得对于一切$n\ge n_0有0\le f(n) \le cg(n)$成立，则成$f(n)$的渐进的上界是$g(n)$，记作$f(n) = Og(n)$

(2)若存在正数c和$n_0$使得对于一切$n\ge n_0有0\le cg(n) \le f(n)$成立，则成$f(n)$的渐进的下界是$g(n)$，记作$f(n) = Og(n)$

(3)若对于任意正数c都存在$n_0$，使得当$n\ge n_0时有0\le f(n)< cg(n)$成立，则记作$f(n)=o(g(n))$

(4)若对于任意正数c都存在$n_0$，使得当$n\ge n_0时有0\ge cg(n)<f(n)$成立，则记作$f(n)=w(g(n))$

(5)若$f(n)=O(g(n))并且f(n) = \Omega(g(n))$,则记作$f(n) = \Theta(g(n))$

上式中“小o记号”和“大O记号”的区别在于，渐进的届中存在等于的可能性，即f(n)和g(n)可以是同一个函数， 我们表示f(n) = o(g(n)),那么f(n) = O(g(n))也是成立的，但是反过来不一定成立。

• 判断两个高阶低阶或者同阶的方法

判断$f(n)和g(n)$的阶，首先计算两函数相除的极限，设$\lim \limits_{n \to \infty}\frac{f(n)}{g(n)}=c$
1. 如果c是某个大于0的常数，那么$f(n) = \Theta(g(n))$
2. 如果c=0，那么$f(n) = o(g(n))$
3. 如果c=$+\infty$，那么$f(n) = w(g(n))$

• 对数运算性质${a^{{log}_{b^n}}} = {n^{{log}_{b^a}}}$

    证明：对上述等式左右取 $log$, 左式得到结果为 $\log_b n$,右边得到${\log_a n}^{\log_b a}$,根据对数计算定理$\log_b n^m = m\log_b n$,于是右边式子转化为$\log_b a\log_a n$,将上述式子中的$\log_a n$表示为 $\frac{\log_b n}{\log_b a}$,这样对右边式子进行化简，结果就是$\log_b n$，左式等于右边式子，上述等式得证。

• 对每个b>1和每个$\alpha$>0，$\log_b n = o(n^\alpha)$

证明：该定理的证明需要用到如下引理：已知f和g是定义域为自然数集合N上的非负函数，

$如果\lim \limits_{n \to \infty}\frac{f(n)}{g(n)}=0，那么f(n) = o(g(n))$

因此，根据上述引理，如果可以证明$\lim \limits_{n \to \infty}\frac{\log_b n}{n^{\alpha}}=0$,那么上述定理可以得证。上述不等式随着n->$\infty$,分子分母都趋于$\infty$,分下列两种情况讨论：
     (1)当$\alpha\ne 1$的时候，采用洛必达法则求解极限。$\log_b n$的倒数为$\frac{1}{n}\ln b$,$n^\alpha$的倒数为${(\alpha-1)n^{\alpha-1}}$,两个于是得到如下推导：

$\lim \limits_{n \to \infty}{\frac{\log_b n}{n^{\alpha}}} = {\frac{\frac{1}{n}\ln b}{{(\alpha-1)n^{\alpha-1}}}} = \frac{\ln b}{(\alpha-1)n^\alpha} = 0$

     (2)当$\alpha =1$的时候，上述极限利用洛必达法则，极限结果是：

$\lim \limits_{n \to \infty}{\frac{\log_b n}{n}} = \frac{\ln b}{n} = 0$

综合两种情况，上述定理得证。上述定义说明只要幂函数的指数大于0，幂函数的阶就会高于对数函数的阶。

• 对每个r>1和每个d>0，有$n^d = o(r^n)$

该结论说明指数函数的增长速度始终大于幂函数，底数越大，指数函数的阶就越高。该定理得证明采用两函数求极限的方法即可得证。

• 对于每个常数d>0,如下结论一定成立：$(logn)^d = o(n)$

证明：该式的证明同样使用洛必达法则，即
$\lim \limits_{n \to \infty}{\frac{(logn)^d}{n}} = \frac{d(logn)^{(d-1)} \ln 2}{n} =...（多次使用洛必达法则）...= 0$

• 主定理 设a>=1,b>1为常数，f(n)为函数，T(n)为非负整数，并且
  $T(n) = aT(n/b)+f(n)$

则有以下结果：
(1). 若 $f(n) = O(n^{log_b {a-\varepsilon}})，\varepsilon \gt 0,那么T(n) = \Theta(n^{log_b a})$。
(2). 若$f(n) = \Theta(n^{log_b a}),那么T(n) = \Theta(n^{log_b a}logn)$。
(3). 若$f(n) = \Omega(n^{logb_a+\varepsilon}),\varepsilon\gt 0$,且对于某个常数$c\lt1$和所有充分大的n有$af(n/b)\le cf(n)$,那么$T(n) = \Omega(f(n)).$

• $2^{\sqrt {2logn}} = O(\sqrt{n})$

证明：对两边同时取log得到左式为$\sqrt{2logn}$，右式为$log\sqrt{n}$。再对两边同时进行平方，左式为$2logn$，右式为${(log\sqrt{n})^2}$。再以2为底，两式为指数，对2进行乘方，此时左式为$n^2 = (\sqrt {n})^4$，右式为${(\sqrt n})^{log\sqrt{n}}$。
显然，左式小于右式，原命题得证。

• 可以通过两边取对数证明的重要结论。
  

1. $n! = o(n^n),$
   
2. $n! = o({2^{2}}^n),$
   
3. $n! = \omega(2^n)$
   
4. ${(log_n)}^d = O(n^k)$, 其中d为任意常数，k为常数
   
5. 斯特林公式 :     $log(n!) = \Theta(nlogn)$

给出一个算法的递推公式，可以计算其复杂度的方法大概有三种：

迭代法

已知$W(n) = W(n-1)+n-1;且满足 W(1) = 0$，迭代法计算如下：

$W(n) = W(n-1)+n-1=W(n-2)+n-2+n-1$
$=W(n-3)+n-3+n-2+n-1+...$
$=W(1)+1+2+3+...+n-3+n-2+n-1$
$=\frac{n(n-1)}{2}$

主定理法

$T(n) = 9T(n/3)+n,T(1) = c,c$是常数
根据主定理，$aT(n/b)$，这里a是9，b是3，${log_3 9}=2,f(n) = n$,根据主定理中第一条，存在$\epsilon >0$使得$n^{2-\epsilon} = \Omega(n)$,于是求得其复杂度为$O(n^2)$

递归树法

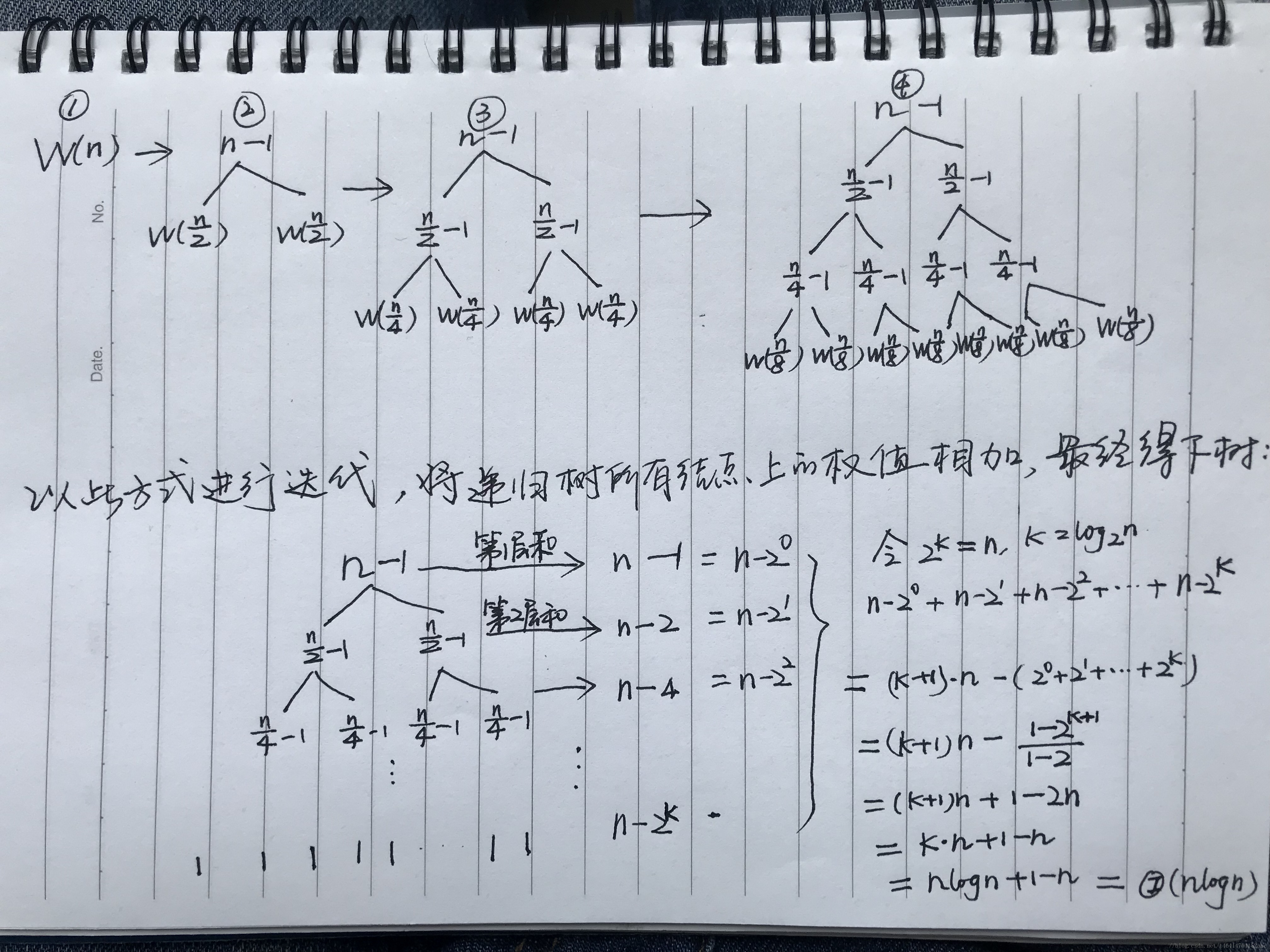
该方法一般在前两种方法无法很好的应用时可以考虑。递归树是一课节点带权的二叉树，初始递归树只有一个结点，标记为权重W(n)，然后不断进行迭代，最后直到树种不再含有权为函数的结点为止，然后将树根结点到树叶节点的全部权值加起来，即为算法的复杂度。以二路归并排序算法的递推方程为例子进行递归树讲解。
已知$W(n) = 2W(n/2)+n-1,并且W(1) = 0$,递归树求解过程如下图：