本篇内容很乱很乱并且没啥逻辑,我的建议是别看!!!!
生存分析-目录
Chapter 1:生存分析-基础知识梳理
一、生存分析基本流程
生存分析常用于研究能够明确划分起止点的现象。
(一)研究目的
(常见研究目的)
a.描述生存过程:绘制出生存曲线、估计生存率、计算中位生存期、平均存活时间等。
b.比较不同处理组的生存率:对于不同的处理组,比较生存率是否有差,如:哪个治疗方案更优。
c.影响因素分析:研究某个或某些因素,对生存率或生存时间的影响作用。
(二)研究内容
确定内容:明确您的研究目的和要回答的问题。
数据收集:确定研究问题及相关的数据,这些数据通常包括个体的生存时间或观察时间,以及是否发生事件的信息(例如,患病或死亡)。
数据处理:对数据进行预处理,包括处理缺失值、异常值和选择合适的变量等。生存数据通常涉及到“右侧截尾”现象,即在研究结束前,部分个体可能还未发生事件,这需要得到妥善处理。
(三)研究方法
参数法(已知生存时间服从某一特定分布,如指数分布,Weibull分布等)、
非参数法(现实中多数生存时间并不符合分布,如KM估计)、
半参数法(规定了影响因素和生存状况间特定的关系,但是没有对时间的分布情况加以限定,如cox比例风险模型);
二、生存分析基本概念
(一)数据类型:删失vs截断
完全数据、删失数据、截断数据(此处我不太能准确描述,仅阐述个人理解)
- 删失数据:只知道试验个体的部分信息,存在信息缺失,但对研究存在一定意义,不能完全删去。如:与样本失去联系、无法观察到结局(死于其他原因)、研究截至时个体仍然活着等。
类型:左删失、右删失、区间删失、广义右删失等;
- 截断数据:在研究中,淘汰了一些对象(样本),使得研究者无法意识到他们的存在。类似“抛弃”,研究中直接排除这部分数据。例如:研究者在研究乳腺癌痊愈时间,规定只研究年龄大于30岁的人,那么患过乳腺癌且在30岁前已经治愈的这部分人群就被截断掉,不用于研究。
类型:左截断、右截断等。
不难看出,截断是主动的,研究者主动进行抉择;删失是被动的,研究者无法控制的。
(二)基本函数
1.累计分布函数F(X)、密度函数f(X)
- 分布函数:反映寿命X的基本分布状况
2.生存函数S(X)
- 生存函数(Survival function):生存时间大于x
S ( x ) = 1 − F ( x ) S(x)=1-F(x) S(x)=1−F(x)
3.危险率函数h(X)
-
危险率函数(Hazard function):(条件风险函数)在x处存活的个体,在下一个单位时间内瞬间死亡的概率
h ( x ) = l i m Δ x → 0 f ( x < X < x + Δ x ∣ X > x ) Δ x h(x)=lim_{\Delta x\rightarrow 0}\frac{f(x<X<x+\Delta x|X>x)}{\Delta x} h(x)=limΔx→0Δxf(x<X<x+Δx∣X>x) -
连续型:
h ( x ) = f ( x ) S ( x ) = − d l n [ S ( x ) ] / d x h(x)=\frac{f(x)}{S(x)}=-dln[S(x)]/dx h(x)=S(x)f(x)=−dln[S(x)]/dx -
离散型: h ( x j ) = 1 − S ( x j ) ) S ( x j − 1 ) h(x_j)=1-\frac{S(x_j))}{S(x_{j-1})} h(xj)=1−S(xj−1)S(xj))
4.累计危险率函数H(X)
-
累计危险率函数
-
连续型:
H ( x ) = ∫ 0 x h ( u ) d u = − l n S ( x ) H(x)=\int_{0}^{x}h(u)du=-lnS(x) H(x)=∫0xh(u)du=−lnS(x) -
离散型:(为了保证函数的连续性)
H ( x ) = ∏ x j ≤ x l n [ 1 − h ( u ) ] H(x)= \prod_{x_j\leq x}ln[1- h(u)] H(x)=xj≤x∏ln[1−h(u)]
(三)常用指标
- 平均剩余寿命(mean residual life)
m r l ( x ) = E ( X − x ∣ X > x ) mrl(x)= E(X-x|X>x) mrl(x)=E(X−x∣X>x) - 连续型: m r l ( x ) = ∫ x ∞ ( u − x ) f ( u ) d u S ( x ) = ∫ x ∞ S ( u ) d u S ( x ) mrl(x)=\frac{\int_{x}^{\infty}(u-x)f(u)du}{S(x)}=\frac{\int_{x}^{\infty}S(u)du}{S(x)} mrl(x)=S(x)∫x∞(u−x)f(u)du=S(x)∫x∞S(u)du
当x=0时,mrl(x)即为生存曲线所围面积(期望)
m r l ( 0 ) = ∫ 0 ∞ u f ( u ) d u = ∫ 0 ∞ S ( u ) d u mrl(0)=\int_{0}^{\infty}uf(u)du=\int_{0}^{\infty}S(u)du mrl(0)=∫0∞uf(u)du=∫0∞S(u)du
- 寿命中位数:
找分位数 S ( x 0.5 ) = 0.5 S(x_{0.5})=0.5 S(x0.5)=0.5
函数关系总结:四个函数可以彼此之间确定
(四)生存时间常见服从分布
1.指数函数
关键:危险率函数为一个常数,与生存时间无关(指数分布的无记忆性)
延申:两参数指数分布
背景:对电子元件,一般存在一个Gurantee time,在该期间不会产生故障,又称作最小存货时间。
2.韦布尔分布(Weibull Distribution)
此时危险率函数不再是常数,因而比指数分布有更广阔的应用
延申:三参数韦布尔分布
3.对数正态分布
危险率函数呈驼峰状,随着生存时间的增加,危险率函数首先达到最大值,随后递减
4.Log-logistic分布
Y=ln(X)服从Logistic分布
当γ>1时,危险率函数在x=0处为0,然后递增,到达峰值后递减
当γ<=1时,危险率函数单调下降
5.Gamma分布
常用于工业可靠性和人类生存的建模问题。其包含了指数分布和卡方分布。
当β>1时,危险率函数随着时间增加,单调上升,称为正老化
当β=1时,危险率函数为常数
当0<β<1时,危险率函数随着时间增加,单调下降,称为负老化
(五)三种常见回归模型(影响因素分析)
Q:为什么要建立回归模型?
A:因为在真实的研究当中,存在着多种多样影响着试验个体生存状态或未来生存前景的因素,
仅研究生存时间X服从的分布是远远不够的,需要建立回归模型以研究这些因素对个体生存的影响。
X X X - 生存时间; W W W - 误差;
Z Z Z - 解释变量/协变量/自变量:影响个体生存状态及未来生存前景的相关因素;
S 0 ( x ) S_0(x) S0(x) - 基本生存函数,除去这些影响因素后,同质的部分;
h 0 ( x ) h_0(x) h0(x) -基本危险率函数,除去这些影响因素后,同质的部分;
1.加速失效模型
令 Y = l n ( X ) Y=ln(X) Y=ln(X)
Y = μ + γ T Z + σ W Y=\mu+ \gamma^T Z +\sigma W Y=μ+γTZ+σW
该式被称为加速失效模型。
Z T ( x ) = ( Z 1 ( x ) , . . , Z p ( x ) ) Z^T(x)=(Z_1(x),..,Z_p(x)) ZT(x)=(Z1(x),..,Zp(x))为解释变量;
W是误差分布,常服从:正态分布(此时X服从对数正态);极值分布(此时X服从Weibull分布);Logistic分布(此时X服从log-logistic分布)。
模型“加速失效”的含义:
已知 S ( x ∣ Z ) = S 0 ( x ⋅ e x p ( μ + σ W ) ) = S 0 ( x ⋅ e x p ( − γ T Z ) ) S(x|Z)=S_0(x\cdot exp(\mu+\sigma W ))=S_0(x\cdot exp(-\gamma^T Z)) S(x∣Z)=S0(x⋅exp(μ+σW))=S0(x⋅exp(−γTZ))
e x p ( − γ T Z ) = 1 , γ T Z = 0 exp( -\gamma^T Z )=1,\gamma^T Z =0 exp(−γTZ)=1,γTZ=0时,没有解释变量,函数回归于X的基础生存函数;
e x p ( − γ T Z ) < 1 , γ T Z > 0 exp( -\gamma^T Z )<1,\gamma^T Z >0 exp(−γTZ)<1,γTZ>0时,生存时间轴被拉长;
e x p ( − γ T Z ) > 1 , γ T Z < 0 exp( -\gamma^T Z )>1,\gamma^T Z <0 exp(−γTZ)>1,γTZ<0时,生存时间周被缩短;
2.乘法危险率模型
h ( x ) = h 0 ( x ) c ( β T Z ) h(x)=h_0(x)c(\beta^TZ) h(x)=h0(x)c(βTZ)
-
h 0 ( x ) h_0(x) h0(x):基本危险率函数
-
c ( β T Z ) c(\beta^TZ) c(βTZ):可以是任何非负函数;
特点:
a.解释变量不同的个两个危险率函数彼此成比例 h ( x ∣ Z 1 ) h ( x ∣ Z 2 ) = c ( β T Z 1 ) c ( β T Z 2 ) \frac{h(x|Z_1)}{h(x|Z_2)}=\frac{c(\beta^T Z_1)}{c(\beta^T Z_2)} h(x∣Z2)h(x∣Z1)=c(βTZ2)c(βTZ1)
b.生存函数: S ( x ∣ Z ) = S 0 ( x ) c ( β T Z ) S(x|Z)=S_0(x)^{c(\beta^T Z)} S(x∣Z)=S0(x)c(βTZ)
延申:Cox成比例危险率回归模型,及 c ( β T Z ) = e x p ( β T Z ) c(\beta^TZ)=exp(\beta^TZ) c(βTZ)=exp(βTZ)
h ( x ∣ Z ) = h 0 ( x ) e x p ( β T Z ) h(x|Z)=h_0(x)exp(\beta^TZ) h(x∣Z)=h0(x)exp(βTZ)
3.加法危险率模型
h ( x ∣ Z ) = h 0 ( x ) + β T ( x ) Z ( x ) h(x|Z)=h_0(x)+\beta^T(x)Z(x) h(x∣Z)=h0(x)+βT(x)Z(x) (3)
其中 h 0 ( x ) h_0(x) h0(x)与 β T ( x ) \beta^T(x) βT(x)都与x有关,相比较乘法危险率模型,人们关注直观暴露出的风险差异
三、非参数法估计
(一)生存函数和累计危险率函数估计
1.生存函数估计
a.无删失情形
经验生存函数: S t ^ = \hat{S_t}= St^=生存时间大于t的个体数/总数
b.存在右删失:Kaplan-Meier估计
- 右删失的表达:
假定 X 1 , X 2 . . . X n X_1,X_2...X_n X1,X2...Xn我们随机抽样n个样本,假定为n个生存时间, C 1 , C 2 . . . C n C_1,C_2...C_n C1,C2...Cn为删失时间,但我们仅能观测到 T 1 , T 2 . . . T n T_1,T_2...T_n T1,T2...Tn,并为后续方便,令 T 1 < T 2 < . . . T n T_1<T_2<...T_n T1<T2<...Tn
T i = m i n ( X i , C i ) T_i=min(X_i,C_i) Ti=min(Xi,Ci)
当样本存在删失时,取 δ i = 0 \delta_i=0 δi=0;样本未删失时,取 δ i = 1 \delta_i=1 δi=1;
KM估计:
-
使用前提:通常当样本容量足够大时,KM曲线会接近真正的生存函数曲线
-
重要假设:删失时间与生存时间独立;
-
生存函数估计表达:
S t ^ = ∏ t i < t ( 1 − 1 n − i + 1 ) δ i \hat{S_t}=\prod _{t_i<t}(1-\frac{1}{n-i+1})^{\delta_i} St^=ti<t∏(1−n−i+11)δi
c.存在重复数据
S t ^ = ∏ t i < t ( 1 − d i Y i ) δ i \hat{S_t}=\prod _{t_i<t}(1-\frac{d_i}{Y_i})^{\delta_i} St^=ti<t∏(1−Yidi)δi
d i d_i di为在 t i t_i ti处死亡的个体数, Y i Y_i Yi为在 t i t_i ti前仍活着的个体数,所以 Y i = Y i − 1 − d i − 1 − c i − 1 Y_i=Y_{i-1}-d_{i-1}-c_{i-1} Yi=Yi−1−di−1−ci−1
方差的Greenwood公式为:
V a r ^ [ S t ^ ] = S t 2 ∑ t i < t d i Y i ( Y i − d i ) \hat{Var}[\hat{S_t}]=S_t^2\sum _{t_i<t}\frac{d_i}{Y_i(Y_i-d_i)} Var^[St^]=St2ti<t∑Yi(Yi−di)di
方差的Aalen&Johansen公式为:
V a r ^ [ S t ^ ] = S t 2 ∑ t i < t d i Y i 2 \hat{Var}[\hat{S_t}]=S_t^2\sum _{t_i<t}\frac{d_i}{Y_i^2} Var^[St^]=St2ti<t∑Yi2di
尾部纠错(待补充):
若最后一个为删失数据,则在用上式计算时,为0,则该样本的信息会被浪费,所以要对尾部进行修正。
d.Nelson-Aelan估计
详细见下方的3
(二)累计危险率函数估计
1.无删失情形
普通公式: S t ^ \hat{S_t} St^从时间t开始的单位区间中死亡的个体数 / 在时间t存活的个体数
精算师常用: S t ^ \hat{S_t} St^从时间t开始的单位区间中死亡的个体数 / 在时间t存活的个体数-1/2*在区间内死亡的人数
2.存在删失
KM估计:由 H ( t ) = − l n [ S ( t ) ] H(t)=-ln[S(t)] H(t)=−ln[S(t)]通过 S t ^ \hat{S_t} St^,求得 H ( t ) ^ \hat{H(t)} H(t)^
3.Nelson-Aelan估计
H ( t ) ^ = ∑ t i < t d i Y i , i f . . . t 1 ≤ t \hat{H(t)}=\sum _{t_i<t}\frac{d_i}{Y_i},if...t_1\leq t H(t)^=ti<t∑Yidi,if...t1≤t
估计式的方差: V a r ^ [ H t ^ ] = ∑ t i < t d i Y i 2 \hat{Var}[\hat{H_t}]=\sum _{t_i<t}\frac{d_i}{Y_i^2} Var^[Ht^]=∑ti<tYi2di
并可由 S t ^ = e x p [ − H ( t ) ^ ] \hat{S_t}=exp[-\hat{H(t)}] St^=exp[−H(t)^]求得到生存函数 S t ^ \hat{S_t} St^的NA估计式。
在小样本情形下,NA估计要比乘积限估计量的效果更好,实际情况下,NA估计通常更为乐观,所以NA估计的 S t ^ \hat{S_t} St^一般大于或等于KM估计。
(三)置信区间
1.生存函数点估计的置信区间
(1)线性区间:适用于大样本情形
大样本情况下,利用的渐进正态性,则100%(1-α)的置信区间估计为:
[ S ( t 0 ) ^ − z 1 − α 2 σ s ( t 0 ) S ( t 0 ) ^ , S ( t 0 ) ^ + z 1 − α 2 σ s ( t 0 ) S ( t 0 ) ^ ] [\hat{S(t_0)}-z_{1-\frac{\alpha}{2}}\sigma _{s}(t_0)\hat{S(t_0)},\hat{S(t_0)}+z_{1-\frac{\alpha}{2}}\sigma _{s}(t_0)\hat{S(t_0)}] [S(t0)^−z1−2ασs(t0)S(t0)^,S(t0)^+z1−2ασs(t0)S(t0)^]
其中:
z 1 − α 2 z_{1-\frac{\alpha}{2}} z1−2α为标准正态分布的1-α/2分位数;
σ s ( t 0 ) = ∑ t i < t d i Y i ( Y i − d i ) = V a r ^ [ S t ^ ] / S t 2 \sigma _{s}(t_0)=\sqrt{\sum _{t_i<t}\frac{d_i}{Y_i(Y_i-d_i)}}=\sqrt{\hat{Var}[\hat{S_t}]/S_t^2} σs(t0)=ti<t∑Yi(Yi−di)di=Var^[St^]/St2
(2)对数变换区间:做出变换,以控制区间在(0,1)之间
[ S ( t 0 ) ^ 1 θ , S ( t 0 ) ^ θ ] [\hat{S(t_0)}^\frac{1}{\theta},\hat{S(t_0)}^\theta] [S(t0)^θ1,S(t0)^θ]
其中: θ = e x p [ z 1 − α 2 σ s ( t 0 ) / l n [ S ( t 0 ) ^ ] ] \theta=exp[z_{1-\frac{\alpha}{2}} \sigma_s(t_0)/ ln[\hat{S(t_0)}] ] θ=exp[z1−2ασs(t0)/ln[S(t0)^]]
(3)反正弦平方根变换区间
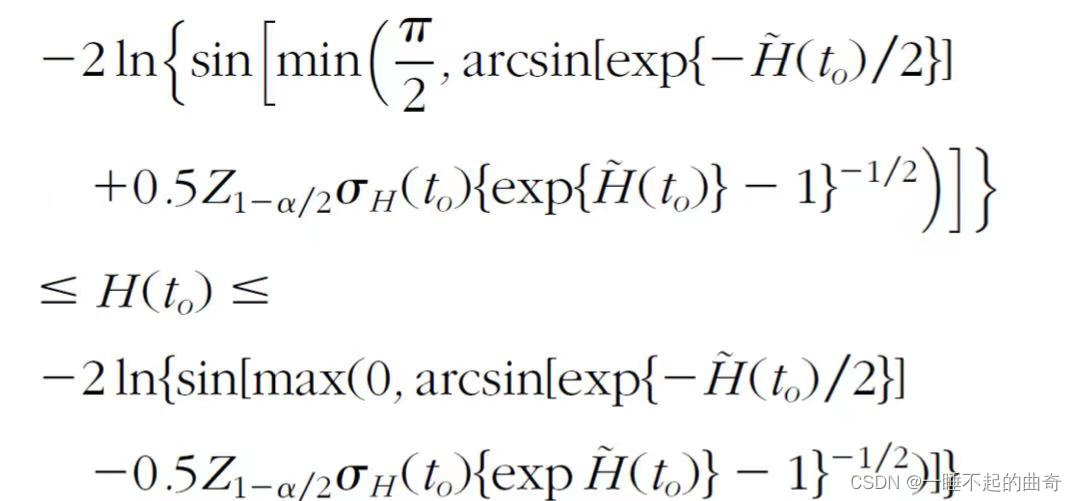
(2)和(3)可适用于小样本情况,(3)更为保守,在样本量小且删失数据多的情况下有较高的可靠性
2.累计危险率函数的置信区间
(四)置信带
1、生存函数置信带
Def 1 − α = P { L ( t ) ⩽ S ( t ) ⩽ U ( t ) } 1-\alpha=P\{L(t)\leqslant S(t) \leqslant U(t)\} 1−α=P{ L(t)⩽S(t)⩽U(t)}则称 [ L ( t ) , U ( t ) ] [L(t), U(t)] [L(t),U(t)]为生存函数的一个(1-α)*100%的置信带。
(1)等概率置信带:
线性变化置信带、对数变化置信带、反正弦平方根变换置信带


(2)Hall&Wellner置信带
2、累计危险函数的置信带
(类似生存函数,也分两类)
(二)生存时间均值、中位数的估计
1.生存时间均值估计
Def: m r l ( 0 ) = ∫ 0 ∞ u f ( u ) d u = ∫ 0 ∞ S ( u ) d u mrl(0)=\int_{0}^{\infty}uf(u)du=\int_{0}^{\infty}S(u)du mrl(0)=∫0∞uf(u)du=∫0∞S(u)du
a.结尾不是删失
-
点估计:用 S ( t ) ^ \hat{S(t)} S(t)^替代上式的 S ( t ) S(t) S(t)
-
前提限制:最大观测值 T n T_n Tn必须为非删失。
b.结尾是删失,解决方案: μ τ ^ = ∫ 0 τ S ( t ) ^ d t \hat{\mu_\tau }=\int_{0}^{\tau}\hat{S(t)}dt μτ^=∫0τS(t)^dt
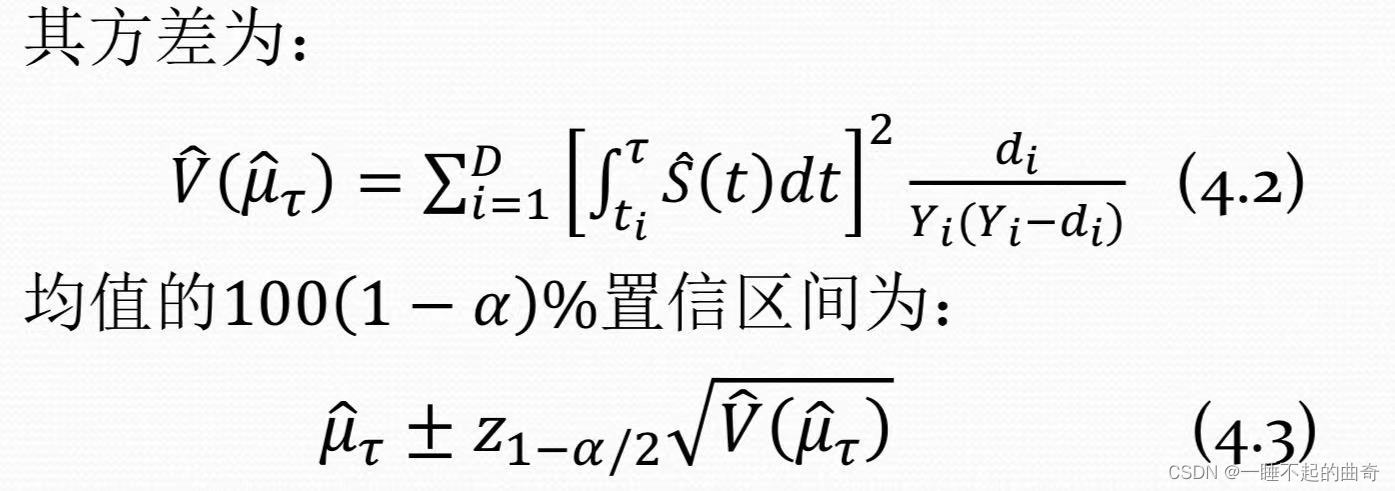
2.生存时间分位点估计
S ( x p ) = 1 − p S(x_p)=1-p S(xp)=1−p
用 S ( t ) ^ \hat{S(t)} S(t)^替代上式的 S ( t ) S(t) S(t)
(三)核函数平滑
在前面的估计当中,均属于粗糙估计,在“尾部”往往存在不稳定,需要进行“修匀”,此时用到核平滑的方法。
随着窗宽的增加,危险率的估计更加平滑,但平滑度的增加会以估计值偏度的增加为代价。所以一般也要使用误差平方积分期望准则等方法寻找最优窗宽。
四、参数估计
(一)图形法
常见三种图形法:概率函数图、危险率函数图、Cox-Snell residual图
-
思想:观察生存时间本身(或变换)与给定的参数分布函数或累计危险函数的图形近似为一条直线。该方法可以满足对生存数据做初步分析的目的。
-
原理:绘制生存时间(或变换函数)与生存时间分布函数(或变换函数)的散点图,判断图形是否近似为直线。
-
步骤:
Step1:选择生存时间满足的分布 Step2:求出生存时间的分布函数估计 Step3:绘制生存时间(或变换)的样本分布函数或其函数的散点图 Step4:做出判断
(二)极大似然估计
五、半参数估计
cox成比例危险率回归模型
Def:(乘法危险率模型的延申)取:
c ( β T Z ) = e x p ( β T Z ) c(\beta^TZ)=exp(\beta^TZ) c(βTZ)=exp(βTZ)
h ( x ∣ Z ) = h 0 ( x ) e x p ( β T Z ) h(x|Z)=h_0(x)exp(\beta^TZ) h(x∣Z)=h0(x)exp(βTZ)
其中: h 0 ( x ) h_0(x) h0(x)是形式完全未知的基准危险函数
之所以要用到COX回归模型,是因为Kaplan-Meier曲线用来对二分类变量差异的可视化比较合适,
但当分类比较多时,如好、中、差、极差,效果不太理想;
而且Kaplan-Meier曲线对连续型变量的风险的可视化不支持。
-----------------------------------------------
Chapter 2:生存分析-实证过程
一、数据集介绍
1.背景介绍
肾导管数据集Kidney catheter data:数据集记录了使用便携式透析设备的肾脏急病患者,在插入导管后复发感染的数据。除了感染以外,导管也可能因为其他原因被移除,这种情况视为删失数据,因而被观测的病人们有完整和删失两种状态。
注:在男性样本当中,有一个编号为21号的患者,其生存时间要远高于他的同类们。如果该样本被移除,没有证据能表明男女患者的生存状态是随机效应的。(即无差别的?)
2.数据描述
数据集:76个样本、7个属性;
- patient: id 病人id
- time: time 生存时间
- status: event status 是否删失
- age: in years 患者年龄
- sex: 1=male, 2=female 患者性别
- disease: disease type (0=GN, 1=AN, 2=PKD, 3=Other) 患病类型
- frail: frailty estimate from original paper 原文章内的脆弱估计
可以看出disease为因子变量,其他均为数值变量
> head(kidney)
id time status age sex disease frail
1 1 8 1 28 1 Other 2.3
2 1 16 1 28 1 Other 2.3
3 2 23 1 48 2 GN 1.9
4 2 13 0 48 2 GN 1.9
5 3 22 1 32 1 Other 1.2
6 3 28 1 32 1 Other 1.2
> class(kidney)
[1] "data.frame"
> str(kidney)
'data.frame': 76 obs. of 7 variables:
$ id : num 1 1 2 2 3 3 4 4 5 5 ...
$ time : num 8 16 23 13 22 28 447 318 30 12 ...
$ status : num 1 1 1 0 1 1 1 1 1 1 ...
$ age : num 28 28 48 48 32 32 31 32 10 10 ...
$ sex : num 1 1 2 2 1 1 2 2 1 1 ...
$ disease: Factor w/ 4 levels "Other","GN","AN",..: 1 1 2 2 1 1 1 1 1 1 ...
$ frail : num 2.3 2.3 1.9 1.9 1.2 1.2 0.5 0.5 1.5 1.5 ...
二、绘制生存曲线
2.1 生存曲线基础知识
2.2 非参数估计
2.2.1 KM估计
####非参数估计
###Survival Function:KM估计
sur_fit_km<-survfit(Surv(time,status)~1,data=kidney)
summary(sur_fit_km)
ggsurvplot(sur_fit_km,conf.int=TRUE,surv.median.line="hv")
估计结果:
该估计结果展示了在样本每个生存时间处的生存概率,标准差及95%的置信区间

使用ggsurvplot绘制的KM生存曲线如下图所示:

注:R默认使用线性置信区间,实际上在小样本下效果较差,并不推荐
2.2.2 NA估计
###Survival Function:NA估计
sur_fit_na<-survfit(formula=Surv(time,status)~1,data=kidney+type="aalen",conf.type="none")
summary(sur_fit_na)
N-A估计结果如图所示:

对比KM结果来看,两者十分接近,但随着生存时间的增加,对survival的估计逐渐增加,标准差较小一些,一般来说,NA估计在小样本情况下效果更好。

三、分组比较
1.KM比较
##KM曲线:计算多个组的生存分布
sex_km<-survfit(Surv(time,status)~sex,data=kidney)
summary(sex_km)
summary(sex_km)$table
#p-value = 0.0039
#绘制K-M曲线
ggsurvplot(sex_km,conf.int=TRUE,
risk.table=TRUE,
surv.median.line="hv",
legend.title = "Sex",
legend.labs = c("Male", "Female"),
pval = TRUE,
break.time.by = 90,
ggtheme = theme_bw(),
xlim=c(0,270))
#conf.int = TRUE,取95%置信区间
#risk.table=TRUE指定是否显示风险表
#surv.median.line表示绘制中位生存时间,hv:同时绘制横坐标和纵坐标,h和v分别代表绘制与横纵坐标平行的直线
使用KM估计画出不同性别的KM曲线,比较其差异。可以看出对于男性的生存曲线明显低于女性,相同时间,男性的存活概率低于女性,危险率更高。

2.Cox回归模型
###COX 回归模型不用于估计生存率,主要用于因素分析
sex_cox <- coxph(Surv(time,status)~sex, data=kidney)
summary(sex_cox)
#p-value=0.00474 **
ggforest(sex_cox)
Cox回归模型结果如下图所示:

用ggforest绘制森林图展示Cox回归分析的结果

3.survival包:Survdiff()
sex_diff<-survdiff(Surv(time,status)~sex,data=kidney,rho = 0)
sex_diff
#p-value=0.004
# With rho = 0 this is the log-rank or Mantel-Haenszel test
# and with rho = 1 it is equivalent to the Peto & Peto modification of the Gehan-Wilcoxon test.
在R的Survival包中有一个Survdiff函数,
检验结果显示:针对不同性别,期望生存时间差异明显,p值=0.004拒绝原假设,认为在不同性别下感染复返的情况有明显差异。

4.参数估计(极大似然估计)
#install.packages("flexsurv")
library("flexsurv")
flexsurvreg(formula=Surv(time,status)~1,data=kidney,dist="exp")
#Log-likelihood = -341.7154, df = 1
#AIC = 685.4308
flexsurvreg(formula=Surv(time,status)~1,data=kidney,dist="weibull")
#Log-likelihood = -341.7154, df = 1
#AIC = 685.4308
flexsurvreg(formula=Surv(time,status)~1,data=kidney,dist="lnorm")
#Log-likelihood = -340.0482, df = 2
#AIC = 684.0963
flexsurvreg(formula=Surv(time,status)~1,data=kidney,dist="llogis")
#Log-likelihood = -342.0464, df = 2
#AIC = 688.0928