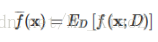预测误差, 或者说泛化误差(generalization error)可以分解为三个部分:
- 偏差(bias)
- 方差(variance)
- 噪声(noise)
在估计学习算法性能的过程中, 我们主要关注偏差与方差. 因为噪声属于不可约减的误差 (irreducible error).
首先抛开机器学习的范畴, 从字面上来看待这两个词:
偏差
这里的偏指的是 偏离 , 那么它偏离了什么导致了误差? 潜意识上, 当谈到这个词时, 我们可能会认为它是偏离了某个潜在的 “标准”, 而这里这个 “标准” 也就是真实情况 (ground truth). 在分类任务中, 这个 “标准” 就是真实标签 (label).
方差
很多人应该都还记得在统计学中, 一个随机变量的方差描述的是它的离散程度, 也就是该随机变量在其期望值附近的 波动程度 . 取自维基百科一般化的方差定义:
如果 X 是一个向量其取值范围在实数空间Rn ,并且其每个元素都是一个一维随机变量,我我们就称 X为随机向量。随机向量的方差是一维随机变量方差的自然推广,其定义为E[(X−μ)(X−μ)T],其中μ=E(X) , XT 是 X 的转置.
先从下面的靶心图来对方差与偏差有个直观的感受
假设红色的靶心区域是学习算法完美的正确预测值, 蓝色点为每个数据集所训练出的模型对样本的预测值, 当我们从靶心逐渐向外移动时, 预测效果逐渐变差.
很容易看出有两副图中蓝色点比较集中, 另外两幅中比较分散, 它们描述的是方差的两种情况. 比较集中的属于方差小的, 比较分散的属于方差大的情况.
再从蓝色点与红色靶心区域的位置关系, 靠近红色靶心的属于偏差较小的情况, 远离靶心的属于偏差较大的情况.
有了直观感受以后, 下面来用公式推导泛化误差与偏差与方差, 噪声之间的关系.
·泛化误差
以回归任务为例, 学习算法的平方预测误差期望为:
·方差
在一个训练集D上模型f对测试样本x的预测输出为f(x;D), 那么学习算法f对测试样本 x的期望预测为:
上面的期望预测也就是针对不同数据集 D , f对x的预测值取其期望,也被叫做 average predicted .
使用样本数相同的不同训练集产生的方差为:
·偏差
期望预测与真实标记的误差称为偏差(bias), 为了方便起见, 我们直接取偏差的平方:
·噪声
噪声为真实标记与数据集中的实际标记间的偏差:
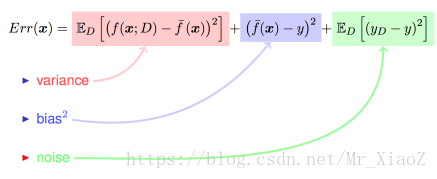
对算法的期望泛化误差进行分解:
不要被上面的公式吓到, 其实不复杂, 在已知结论的情况下, 了解每一项的意义, 就是一个十分简单的证明题而已, 蓝色部分是对上面对应的等价替换, 然后对其展开后, 红色部分刚好为 0.
对最终的推导结果稍作整理:
至此, 继续来看一下偏差, 方差与噪声的含义 [^2]:
偏差:度量了学习算法的期望预测与真实结果的偏离程度, 刻画了学习算法本身的拟合能力
方差:度量了同样大小的训练集的变动所导致的学习性能的变化, 即刻画了数据扰动所造成的影响
噪声:表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界, 即 刻画了学习问题本身的难度 . 巧妇难为无米之炊, 给一堆很差的食材, 要想做出一顿美味, 肯定是很有难度的.
想当然地, 我们希望偏差与方差越小越好, 但实际并非如此. 一般来说, 偏差与方差是有冲突的, 称为偏差-方差窘境 (bias-variance dilemma).
给定一个学习任务, 在训练初期, 由于训练不足, 学习器的拟合能力不够强, 偏差比较大, 也是由于拟合能力不强, 数据集的扰动也无法使学习器产生显著变化, 也就是欠拟合的情况;
随着训练程度的加深, 学习器的拟合能力逐渐增强, 训练数据的扰动也能够渐渐被学习器学到;充分训练后, 学习器的拟合能力已非常强, 训练数据的轻微扰动都会导致学习器发生显著变化, 当训练数据自身的、非全局的特性被学习器学到了, 则将发生过拟合.