【机器视觉】1. 张正友平面标定[转]

张正友的平面标定方法是介于传统标定方法和自标定方法之间的一种方法。它既避免了传统方法设备要求高，操作繁琐等缺点，又较自标定方法精度高，因此张氏标定法被广泛应用于计算机视觉方面，本文尝试对这一标定方法做一介绍。包括：

模型，即如何由光学成像公式和坐标变换方法建立摄像机的参数矩阵
算法，即如何对参数矩阵进行计算
优化，即如何计算畸变，以及如何对参数进行优化

一、坐标变换

定义[位置（position）描述]
在三维坐标系A下确定空间中一点的位置，用一个 $3\times 1$ 的矢量表示为 ${}^A {}P=(x_A,y_A,z_A)^T$
定义[姿态（orientation）描述]
在物体上固定一个坐标系B，给出此坐标系相对于参考坐标系A的表达，即在坐标系A中表达坐标系B的三个单位矢量 ${}^A \boldsymbol{x_B}=\begin{pmatrix}x_B \cdot x_A\\ x_B \cdot y_A\\ x_B \cdot z_A\end{pmatrix}\quad {}^A \boldsymbol{y_B}=\begin{pmatrix}y_B \cdot x_A\\ y_B \cdot y_A\\ y_B \cdot z_A\end{pmatrix}\quad {}^A \boldsymbol{z_B}=\begin{pmatrix}z_B \cdot x_A\\ z_B \cdot y_A\\ z_B \cdot z_A\end{pmatrix}$
用旋转矩阵 ${}{_B^A}{}R=({}^A \boldsymbol{x_B}, {}^A \boldsymbol{y_B}, {}^A \boldsymbol{z_B})^T$
描述姿态。
定义[位姿（pose）描述]
位置描述和姿态描述统称为位姿（pose）描述。将坐标系B固定在物体上，并考察坐标系B相对于参考坐标系A的位姿，用 ${}^A {P_{OB}}$ 表示坐标系B的原点在坐标系A中的位置矢量，用旋转矩阵 ${}{_B^A}{}R$ 表示姿态，那么B相对于A的旋转 $\boldsymbol{B}=({}{_B^A}{}R,{}^A {P_{OB}})$
旋转矩阵的性质

- ${}{_B^A}{}R=({}^A \boldsymbol{x_B}, {}^A \boldsymbol{y_B}, {}^A \boldsymbol{z_B})^T=\begin{pmatrix}{}{^B}{\boldsymbol{x}_A^T} \\ {}{^B}{\boldsymbol{y}_A^T} \\ {}{^B}{\boldsymbol{z}_A^T} \end{pmatrix}$
- 旋转矩阵中的9个元素只有3个是独立的
旋转矩阵是单位正交矩阵， ${}^A \boldsymbol{x_B}, {}^A \boldsymbol{y_B}, {}^A \boldsymbol{z_B}$ 是单位矢量，且相互垂直
- $\text{det} ({}{_B^A}{}R)=1, {}{_B^A}{R^{-1}}={}{_B^A}{R^{T}}={}{^B_A}{}R$

定义[平移坐标变换]
只变换位置不变换姿态 ${}^A {}P={}{^B}{}P+{}^A {P_{OB}}$
定义[旋转坐标变换]
只变换姿态不变换位置，两个坐标系原点相同 ${}^A {}P={}{_B^A}{}R {}{^B}{}P$
一般坐标变换（位姿变换）方程 ${}^A {}P={}{_B^A}{}R {}{^B}{}P+{}^A {P_{OB}}$

定义[齐次坐标变换]
用 $4 \times 1$ 的列矢量表示三维空间中的点，称为点的齐次坐标 (Homogeneous coordinate)，即 $P=(x,y,z,1)^T$ ，那么齐次变换矩阵 ${}{_B^A}{}T=\begin{pmatrix}{}{_B^A}{}R & {}^A {P_{OB}}\\ \boldsymbol{0} & 1\end{pmatrix}$
且 ${}{_C^A}{}T={}{_B^A}{}T {}{_C^B}{}T$
使用齐次坐标的目的，是为了利用矩阵变换，不仅能表示伸缩与旋转，还能够表示平移。三维点的齐次坐标有形如[x,y,z,w]的形式，设w=1，此时相当于我们把3维的坐标平移搬去了w=1的平面上，也就是4维空间的点投影到w=1平面上，齐次坐标映射的3D坐标是（x/w,y/w,z/w），也就是（x,y,z）；（x,y,z）在齐次空间中有无数多个点与之对应。所有点的形式是（kx,ky,kz,k），其轨迹是通过齐次空间原点的“直线”，而每个点相当于3维的世界坐标。
当w=0时，可解释为无穷远的“点”，其意义是描述方向。这也是平移变换的开关，当w=0时，此时不能平移变换了。这个现象是非常有用的，因为有些向量代表“位置”，应当平移，而有些向量代表“方向”，如表面的法向量，不应该平移。从几何意义上说，能将第一类数据当作”点”，第二类数据当作”向量”。可以通过设置w的值来控制向量的意义。
下面对旋转运动的表示与转换进行讨论。
方向余弦矩阵可以用来表示两个坐标系之间的旋转，同样也可以用来表示一个向量绕相同坐标系中某个轴的旋转。讨论一下当它表达两个坐标系之间的选择时的定义方式，如下，假设两组坐标系的基底，分别为： $\vec v = (\vec {{i}_{0}},\vec {{j}_{0}},\vec {{k}_{0}})\quad \vec u = (\vec {{i}_{1}},\vec {{j}_{1}},\vec {{k}_{1}})$

另外，假设有一个向量a ，那么a 在这两组基底下的投影为： $\vec a=\vec v\cdot a_{v}=\vec u\cdot a_{u}$

则 $C=\vec v^{T}\cdot\vec u = \begin{pmatrix} \vec {{i}_{0}}\cdot\vec {{i}_{1}} & \vec {{i}_{0}}\cdot\vec {{j}_{1}} & \vec {{i}_{0}}\cdot\vec {{k}_{1}} \\ \vec {{j}_{0}}\cdot\vec {{i}_{1}} & \vec {{j}_{0}}\cdot\vec {{j}_{1}} & \vec {{j}_{0}}\cdot\vec {{k}_{1}} \\ \vec {{k}_{0}}\cdot\vec {{i}_{1}} & \vec {{k}_{0}}\cdot\vec {{j}_{1}} & \vec {{k}_{0}}\cdot\vec {{k}_{1}} \end{pmatrix}$ $a_{v}=\vec v^{T}\cdot\vec u \cdot a_{u}=a_{v}=C\cdot a_{u}$
欧拉角适合用于表示两个坐标系之间的旋转。欧拉角方法根据一切旋转都能分解为三次绕空间中不同轴的旋转的原理，表明了一切坐标系的取向，都可以用三个欧拉角来表示。

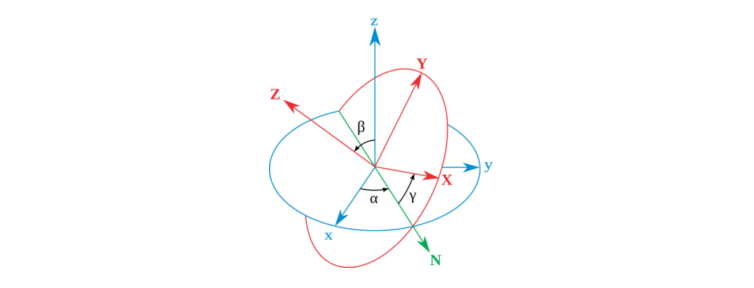欧拉角

事实上，欧拉角法可以分为两类，一类是依次旋转三个不同的轴，称为Tait-Bryan

angles，因此可选顺序有：X-Y-Z，X-Z-Y，Y-X-Z，Y-Z-X，Z-X-Y，Z-Y-X；另一类是相邻两次旋转不同的轴，也就是上文介绍的那一类，称为Euler

angles，可选顺序有：X-Y-X，X-Z-X，Y-X-Y，Y-Z-Y，Z-X-Z，Z-Y-Z。由于绕不同的轴旋转最后得到的欧拉角是不同的，因此在用到欧拉角的场合必须指明旋转的顺序。欧拉角表示方法中其实还存在外在旋转和内在旋转的区别，前者是指每次围绕的旋转轴是原始坐标系的轴，后者则是围绕旋转后得到的坐标系的轴。
设欧拉角的旋转顺序与方式为Z-Y-X，并且是内在旋转。下面，我们来推导由欧拉角到旋转矩阵的转换关系。
绕Z轴旋转 $\psi$ 角度（从n系到1系），即偏航角(yaw)
${}{_{n}^{1}}{}\boldsymbol{R} = \begin{pmatrix} \cos{\psi} & \sin{\psi} & 0 \\ -\sin{\psi} & \cos{\psi} & 0 \\ 0 & 0 & 1 \end{pmatrix}$
绕Y轴旋转 $\theta$ 角度（从1系到2系），即俯仰角(pitch)
${}{_{1}^{2}}{}\boldsymbol{R} = \begin{pmatrix} \cos{\theta} & 0 & -\sin{\theta} \\ 0 & 1 & 0 \\ \sin{\theta} & 0 & \cos{\theta} \end{pmatrix}$
绕X轴旋转 $\gamma$ 角度（从2系到b系），即滚转角(roll)
${}{_{2}^{b}}{}\boldsymbol{R} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos{\gamma} & \sin{\gamma} \\ 0 & -\sin{\gamma} & \cos{\gamma} \end{pmatrix}$
则
${}{_{n}^{b}}{}\boldsymbol{R} = {}{_{2}^{b}}{}\boldsymbol{R} \cdot {}{_{1}^{2}}{}\boldsymbol{R} \cdot {}{_{n}^{1}}{}\boldsymbol{R} =\begin{pmatrix} \cos{\theta} \cos{\psi} & \cos{\theta} \sin{\psi} & -\sin{\theta} \\ \sin{\theta} \sin{\gamma} \cos{\psi} - \cos{\gamma} \sin{\psi} & \sin{\theta} \sin{\gamma} \sin{\psi} + \cos{\gamma} \cos{\psi} & \cos{\theta} \sin{\gamma} \\ \sin{\theta} \cos{\gamma} \cos{\psi} + \sin{\gamma} \sin{\psi} & \sin{\theta} \cos{\gamma} \sin{\psi} - \sin{\gamma} \cos{\psi} & \cos{\theta} \cos{\gamma} \end{pmatrix}$
以上便定义了由欧拉角到旋转矩阵的转换关系。

二、摄像机模型

摄像机模型中的几个坐标系

-[世界坐标系(w)] 参考坐标系/基准坐标系，用于描述摄像机和物体的位置
-[摄像机坐标系(c)] 固定在摄像机上，原点在光心，Zc轴沿光轴方向， Xc/Yc轴分别平行于成像平面
-[以物理单位表示的图像坐标系 (x, y)] 原点在摄像机光轴与图像平面的交点，x/y轴与摄像机Xc/Yc轴平行，沿图像平面方向
-[以像素为单位表示的图像坐标系 (u, v)] 原点在数字图像的左上角，u/v轴沿图像平面向右向下为正方向

首先考虑小孔摄相机模型，记空间点在摄像机坐标系中的齐次坐标为 $X_c=(x_c, y_c, z_c, 1)^T$ ，它的像点在图像坐标系中的齐次坐标记为 $m=(x, y, 1)^T$ ，相机焦距为f，根据相似三角形有
$\begin{cases} x=\frac{fx_c}{z_c} \\ y=\frac{fy_c}{z_c} \end{cases}$
即
$z_cm = \begin{pmatrix} f_x \\ f_y \\ 1 \end{pmatrix}= \begin{pmatrix} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \end{pmatrix}X_c$
小孔摄相机模型将物体从摄像机坐标系转换到xy坐标系表示，下面我们需要将点向uv坐标系转换，也就是图像数字化。通常我们获取得到的图像是CCD摄像机采集的数字图像，CCD相机是将图像平面的点进行数字离散化。设CCD摄像机数字离散化后的像素是一个矩形，矩形的长与宽分别为dx，dy；主点不是图象坐标系原点，在图像坐标系中坐标为
$(x_0, y_0, 1)^T$ ，则 $(u_0,v_0)^T=(x_0/d_x,y_0/d_y)^T$ 为CCD摄像机的主点
$1^{\circ}$ 当uv轴互相垂直时，则
$\begin{cases} u=\frac{x}{d_x} +u_0\\ v=\frac{y}{d_y} +v_0 \end{cases}\Rightarrow \begin{pmatrix} u \\ v \\ 1 \end{pmatrix}= \begin{pmatrix}\frac{1}{d_x} & 0 & u_0 \\ 0 & \frac{1}{d_y} & v_0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}$

则摄像机内参数矩阵
$K=\begin{pmatrix}\frac{1}{d_x} & 0 & u_0 \\ 0 & \frac{1}{d_y} & v_0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} f & 0 & 0 \\ 0 & f & 0 \\ 0 & 0 & 1 \end{pmatrix}=\begin{pmatrix}k_x & 0 & u_0 \\ 0 & k_y & v_0 \\ 0 & 0 & 1 \end{pmatrix}$

其中
$\begin{cases}k_x=f/d_x\\ k_y=f/d_y\end{cases}$

称为CCD摄像机在u轴和v轴方向上的尺度因子。
$2^{\circ}$ 当uv轴有夹角 $\theta$ 时，则
$\begin{cases} u=\frac{x-y\text{cot} \theta}{d_x} +u_0\\ v=\frac{y}{d_y \sin \theta} +v_0 \end{cases}\Rightarrow \begin{pmatrix} u \\ v \\ 1 \end{pmatrix}= \begin{pmatrix}\frac{1}{d_x} & -\frac{1}{d_x\tan \theta} & u_0 \\ 0 & \frac{1}{d_y\sin \theta} & v_0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}$
则摄像机内参数矩阵
$K=\begin{pmatrix}\frac{1}{d_x} & -\frac{1}{d_x\tan \theta} & u_0 \\ 0 & \frac{1}{d_y\sin \theta} & v_0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} f & 0 & 0 \\ 0 & f & 0 \\ 0 & 0 & 1 \end{pmatrix}=\begin{pmatrix}k_x & k_s & u_0 \\ 0 & k_y & v_0 \\ 0 & 0 & 1 \end{pmatrix}$
其中
$\begin{cases}k_x=f/d_x\\ k_y=f/(d_y\sin \theta)\\ k_s=-k_x /\tan \theta\end{cases}$
以上推导出了摄像机内参数模型，然而，我们一般描述一个三维点，由于相机可能一直在运动，所以我们并不是基于摄像机坐标系下对其描述。我们通常是在世界坐标系下进行描述。摄像机外参数模型就是将物体在世界坐标系中的位置，变换到摄像机坐标系下。摄像机外参数矩阵是一个四阶矩阵
${}{_w^c} M=\begin{pmatrix}{}{_w^c}{}R & {}{^c}P_{Ow} \\ 0^T & 1\end{pmatrix}$
则摄像机参数矩阵（单应矩阵）
$M_{3\times 4}=(K,\boldsymbol{0})\cdot {}{_w^c} M$

三、直接线性变换（DLT）标定

定义[单应性变换]
单应性变换（homography transform）就是一个平面到另一个平面的映射关系。在标定问题里，单应矩阵包括摄像机内外参数矩阵。
我们先举一个简单的例子。在图像拼接中，得到了两张图像的特征匹配，两个点集分别记作X和X'；用单应性变换来拟合二者的关系，可表达为 $c\begin{pmatrix}u\\v\\1\end{pmatrix}=H\begin{pmatrix}x\\y\\1\end{pmatrix}$ 其中 $\begin{pmatrix}u&v&1\end{pmatrix}^T$ 是X'中特征点的坐标， $\begin{pmatrix}x&y&1\end{pmatrix}^T$ 是X中特征点的坐标，H即是单应性矩阵，代表它们之间的变换关系。H是个3×3的矩阵，有8个自由度，所以待求未知参数有8个 $H=\begin{pmatrix}h_1&h_2&h_3\\h_4&h_5&h_6\\h_7&h_8&h_9\end{pmatrix}$ 则
$\begin{cases} -h_1 x-h_2 y-h_3 +(h_7 x+h_8 y +h_9)u=0\\ -h_4 x-h_5 y-h_6 +(h_7 x+h_8 y +h_9)v=0 \end{cases}$
整理为Ah=0的形式，其中
$A=\begin{pmatrix}-x&-y&-1&0&0&0&ux&uy&u\\0&0&0&-x&-y&-1&vx&vy&v\end{pmatrix}$
$h=\begin{pmatrix}h_1&h_2&h_3&h_4&h_5&h_6&h_7&h_8&h_9\end{pmatrix}^T$
由未知变量的个数可知，求解出H至少需要4对匹配点。通常情况下为了得到更稳定的结果，会用到多于4对的特征匹配。所以，这个方程会变成超定的，可以将最小二乘解作为最后的解。方程的最小二乘解有一个既定的结论，即对A进行SVD分解，A的最小的奇异值对应的右奇异向量即是h的解。
证明：解方程Ah=0等价于优化问题 $\min \|Ah\| \\ \text{s.t. } \|h\|=1$

因为U是单位正交矩阵，所以 $\|Ah\|=\|U\Sigma V^T h\|=\|\Sigma V^T h\|$

令 $y=V^T h$ ，则方程等价于
$\min \|\Sigma y\| \\ \text{s.t. } \|y\|=1$
由于 $\Sigma$ 是一个对角矩阵，对角元的元素按递减的顺序排列，因此最优解在 $y = (0, 0,..., 1)^T$ 取得，就是V的最小奇异值对应的列向量，即V的最后一列。Q.E.D.
回到标定问题，当uv坐标系中u垂直于v时，若不考虑畸变，那么 $z_c \begin{pmatrix} u \\ v \\ 1 \end{pmatrix}=\begin{pmatrix}k_x & 0 & u_0 &0\\ 0 & k_y & v_0 &0\\ 0 & 0 & 1 &0\end{pmatrix}\begin{pmatrix} {}{_w^c}{}R & {}{^c}P_{Ow} \\ 0^T & 1 \end{pmatrix}\begin{pmatrix} x_w \\ y_w \\z_w \\1 \end{pmatrix}$
摄像机矩阵
$M=\begin{pmatrix} m_{11} & m_{12} & m_{13} & m_{14}\\m_{21} & m_{22} & m_{23} & m_{24}\\m_{31} & m_{32} & m_{33} & m_{34} \end{pmatrix}$
将M的元素作为未知数，矩阵展开消去 $z_c$ ，对于n个已知的空间点，得到2n个关于M的方程
$A_{2n\times 11}(m_{11},m_{12},...,m_{33})^T=(u_1 m_{34},v_1 m_{34},...,u_n m_{34},v_n m_{34})^T$
设 $m'=\frac{1}{m_{34}} (m_{11},m_{12},...,m_{33})^T,b=(u_1 ,v_1 ,...,u_n ,v_n)^T$
则 $m'=(A^T A)^{-1} A^T b$ 在相差一个常数因子 $m_{34}$ 的前提下，确定M，设 $m_i'=(m_{i1}',m_{i2}',m_{i3}')^T$ ，平移向量 $t={}{^c}P_{Ow}=(t_x,t_y,t_z)^T$ 旋转矩阵 $R=\begin{pmatrix} r_1^T \\ r_2^T \\ r_3^T \end{pmatrix}$ 则
$\begin{gather} m_{34}=\frac{1}{||m_3'||}\\u_0=m_{34}^2 m_1'{}{^T}m_3'\quad v_0=m_{34}^2 m_2'{}{^T}m_3'\\k_x=m_{34}^2 ||m_1'\times m_3'||\quad k_y=m_{34}^2 ||m_2'\times m_3'||\\t_x=\frac{m_{34}(m_{14}'-u_0)}{k_x}\quad t_y=\frac{m_{34}(m_{24}'-v_0)}{k_y}\quad t_z=m_{34}\\r_1=\frac{m_{34}(m_1'-u_0m_3')}{k_x}\quad r_2=\frac{m_{34}(m_2'-v_0m_3')}{k_y}\quad r_3=m_{34} m_3' \end{gather}$

四、张氏标定法：摄像机参数的估计

张正友平面标定法的前提

- 认为内参数矩阵 $K=\begin{pmatrix}k_x & k_s & u_0 \\ 0 & k_y & v_0 \\ 0 & 0 & 1 \end{pmatrix}$
- 标定物：平面靶标
- 将世界坐标系置于靶标平面，原点设在靶标一角，Xw/Yw方向沿靶标平面，Zw方向垂直于靶标平面
- 先不考虑畸变，标定摄像机参数，得到参数的线性初值；然后利用线性初值，进行非线性标定，得到畸变参数
因此，在
$z_c \begin{pmatrix} u \\ v \\ 1 \end{pmatrix}=\begin{pmatrix}k_x & k_s & u_0 &0\\ 0 & k_y & v_0 &0\\ 0 & 0 & 1 &0\end{pmatrix}\begin{pmatrix} {}{_w^c}{}R & {}{^c}P_{Ow} \\ 0^T & 1 \end{pmatrix}\begin{pmatrix} x_w \\ y_w \\z_w \\1 \end{pmatrix}$
中令 $z_w=0$ ， ${}{^c}P_{Ow}=t,{}{_w^c}{}R=(r_1,r_2,r_3)$ 则
$z_c \begin{pmatrix} u \\ v \\ 1 \end{pmatrix}=\begin{pmatrix}k_x & k_s & u_0 \\ 0 & k_y & v_0 \\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} r_1 & r_2 & t \end{pmatrix}\begin{pmatrix} x_w \\ y_w \\1 \end{pmatrix}=H\begin{pmatrix} x_w \\ y_w \\1 \end{pmatrix}$
令
$H=\begin{pmatrix}h_1^T \\ h_2^T \\ h_3^T\end{pmatrix}\quad P_i=\begin{pmatrix}x_i\\y_i\\1\end{pmatrix}$
则
$\begin{pmatrix} P_i^T & 0 & -u_i P_i^T\\0 & P_i^T & v_i P_i^T \end{pmatrix}\begin{pmatrix} h_1 \\ h_2 \\h_3 \end{pmatrix}=0$
对于n个特征点
$\begin{pmatrix} P_1^T & 0 & -u_1 P_1^T\\0 & P_1^T & v_1 P_1^T\\ \vdots & \vdots & \vdots \\P_n^T & 0 & -u_n P_n^T\\0 & P_n^T & v_n P_n^T \end{pmatrix}\begin{pmatrix} h_1 \\ h_2 \\h_3 \end{pmatrix}=A\begin{pmatrix} h_1 \\ h_2 \\h_3 \end{pmatrix}=0$
对A进行SVD分解，即$A=U\Sigma V^T$，则以上方程的解是V的最后一列。

假如考虑噪声影响，假设噪声为零均值高斯噪声，方差矩阵为 $\Sigma_i$ ，由最大似然估计求解单应矩阵H，或定义目标函数F，求解H 使F取到最小
$\min F=\sum_{i=1}^n (Q_i-\hat Q_i)^T \Sigma_i (Q_i-\hat Q_i) \quad Q_i=\begin{pmatrix} u_i \\ v_i \end{pmatrix}\hat Q_i=(h_3^T P_i)^{-1}\begin{pmatrix} h_1^T P_i\\h_2^T P_i \end{pmatrix}$
实际应用中假设 $\Sigma_i=\sigma_i^2 I$ ，则 $F=\sum_{i=1}^n ||Q_i-\hat Q_i||^2$ 使用不考虑噪声情况下得到的单应矩阵H作为初值计算 $\hat Q_i$ 通过Levenburg-Marquardt算法求出H的最终解。
H是一个齐次矩阵，所以有8个未知数，至少需要8个方程，每对对应点能提供两个方程，所以至少需要四个对应点，就可以算出世界平面到图像平面的单应性矩阵H。这样得到的H，计算结果与真实解相差一个常数因子，即
$H=(h_1\ h_2\ h_3) = \lambda K(r_1\ r_2\ t)$
那么
$\begin{cases} r_1=\frac{1}{\lambda}K^{-1}h_1 \\ r_2=\frac{1}{\lambda}K^{-1}h_2 \end{cases}$
由于旋转矩阵是个酉矩阵， $r_1$ 和 $r_2$ 正交，即
$\begin{cases} r_1^Tr_2=0 \\ ||r_1||=||r_2||=1 \end{cases}$
可得约束条件
$\begin{cases} h_1^TK^{-T}K^{-1}h_2=0 \\ h_1^TK^{-T}K^{-1}h_1 = h_2^TK^{-T}K^{-1}h_2 \end{cases}$
即每个单应性矩阵能提供两个方程，而内参数矩阵包含5个参数，要求解，至少需要3个单应性矩阵。为了得到三个不同的单应性矩阵，我们使用至少三幅棋盘格平面的图片进行标定。通过改变相机与标定板之间的相对位置来得到三个不同的图片。假如只有两幅图片，那么 $k_s$ 将不能估计，也就是认为数字图像坐标系uv相互垂直（ $k_s =0$ ）。记
$K=\begin{pmatrix} \alpha & \gamma & u_0 \\ 0 & \beta & v_0 \\ 0 & 0 & 1 \end{pmatrix}$
则
$B=K^{-T}K^{-1}= \begin{pmatrix} B_{11} & B_{12} & B_{13} \\ B_{21} & B_{22} & B_{23} \\ B_{31} & B_{32} & B_{33} \end{pmatrix}= \begin{pmatrix} \frac{1}{\alpha^2} & -\frac{\gamma}{\alpha^2\beta} & \frac{v_0\gamma-u_0\beta}{\alpha^2\beta} \\ -\frac{\gamma}{\alpha^2\beta} & \frac{\gamma^2}{\alpha^2\beta^2}+\frac{1}{\beta^2} & -\frac{\gamma(v_0\gamma-u_0\beta)}{\alpha^2\beta^2}-\frac{v_0}{\beta^2} \\ \frac{v_0\gamma-u_0\beta}{\alpha^2\beta} & -\frac{\gamma(v_0\gamma-u_0\beta)}{\alpha^2\beta^2}-\frac{v_0}{\beta^2} & \frac{(v_0\gamma-u_0\beta)^2}{\alpha^2\beta^2}+\frac{v_0}{\beta^2}+1 \end{pmatrix}$
可以看到，B是一个对称阵，所以B的有效元素为六个，让这六个元素写成向量b，即
$b=\begin{pmatrix} B_{11} & B_{12} & B_{22} & B_{13} & B_{23} & B_{33} \end{pmatrix}^T$
那么
$h_i^TBh_j = v^T_{ij}b \\ \text{where } v_{ij}=\begin{pmatrix} h_{i1}h_{j1} & h_{i1}h_{j2}+h_{i2}h_{j1} & h_{i2}h_{j2} & h_{i3}h_{j1}+h_{i1}h_{j3} & h_{i3}h_{j2}+h_{i2}h_{j3} & h_{i3}h_{j3} \end{pmatrix}^T$
利用约束条件可得
$\begin{pmatrix} v^T_{12} \\ (v_{11}-v_{22})^T \end{pmatrix} b=0$
我们至少需要三幅包含棋盘格的图像，可以计算得到B，然后通过Cholesky分解得到相机的内参数矩阵K，首先计算出
$v_0=\frac{B_{12} B_{13}- B_{11} B_{23}}{B_{11}B_{22}-B_{12}^2}$
然后定义
$c=B_{33}-\frac{B_{13}^2 + v_0 (B_{12} B_{13}- B_{11} B_{23})}{B_{11}}$
于是内参数
$\begin{gather} k_x=\alpha=\sqrt{\frac{c}{B_{11}}}\\k_y=\beta=\sqrt{\frac{cB_{11}}{B_{11}B_{22}-B_{12}^2}}\\k_s=\gamma=\frac{-B_{12} \alpha^2 \beta}{c}\\u_0=\frac{\gamma v_0}{\beta}-\frac{B_{13} \alpha^2}{c} \end{gather}$
而外参数
$\begin{gather} \lambda =\frac{1}{\|K^{-1}h_1\|}=\frac{1}{\|K^{-1}h_2\|} \\ r_1=\frac{1}{\lambda}K^{-1}h_1 \\ r_2=\frac{1}{\lambda}K^{-1}h_2 \\ r_3 = r_1 \times r_2 \\ t=\lambda K^{-1}h_3 \end{gather}$
考虑到R是单位正交阵，因此对R进行奇异值分解就有 $R\approx UIV^T =UV^T$ ，其中U和V通过对 $R^T R$ 的特征向量作正交化单位化得到。

五、张氏标定法：畸变的估计

张氏标定法只关注了影响最大的径向畸变，并忽略四阶以上的畸变量
$\begin{cases} x_d =x_u[1+k_1(x_u^2+y_u^2)+k_2(x_u^2+y_u^2)^2]\\y_d =y_u[1+k_1(x_u^2+y_u^2)+k_2(x_u^2+y_u^2)^2] \end{cases}$
其中 $(x_d,y_d)$ 表示角点在成像面上的实际坐标， $(x_u,y_u)$ 表示角点在成像面上的理想坐标。将畸变模型转换到数字图像坐标进行求解
$\begin{cases} \hat u = u_0 + \alpha x_d + \gamma y_d \\ \hat v = v_0 + \beta y_d \end{cases}$
其中，(u,v)是理想的像素坐标， $(\hat u,\hat v)$ 是实际的像素坐标。 $(u_0,v_0)$ 代表主点，则
$\begin{cases} \hat u = u + (u-u_0)[k_1(x_u^2+y_u^2)+k_2(x_u^2+y_u^2)^2] \\ \hat v = v + (v-v_0)[k_1(x_u^2+y_u^2)+k_2(x_u^2+y_u^2)^2] \end{cases}$
即
$\begin{pmatrix} (u-u_0)(x_u^2+y_u^2) & (u-u_0)(x_u^2+y_u^2)^2 \\ (v-v_0)(x_u^2+y_u^2) & (v-v_0)(x_u^2+y_u^2)^2 \end{pmatrix}\begin{pmatrix}k_1 \\ k_2 \end{pmatrix}= \begin{pmatrix} \hat u -u \\ \hat v -v \end{pmatrix}$
简记为 $Dk=d$
那么
$k=[k_1\ k_2]^T = (D^TD)^{-1}D^Td$
上述的推导结果是基于理想情况下的解，但由于可能存在高斯噪声，所以使用最大似然估计进行优化。设我们采集了n副包含棋盘格的图像进行定标，每个图像里有棋盘格角点m个。令第i副图像上的角点 $M_{ij}$ 在上述计算得到的摄像机矩阵下图像上的投影点为：
$\hat{m}(K,R_i,t_i,M_{ij}) = K(R|t)M_{ij}$
其中Ri和ti是第i副图对应的旋转矩阵和平移向量，K是内参数矩阵。则角点的概率密度函数为：
$f(m_{ij})=\frac{1}{\sqrt{2\pi}}\exp \left(\frac{-(\hat{m}(K,R_i,t_i,M_{ij})-m_{ij})^2}{\sigma^2}\right)$
似然函数
$L(A,R_i,t_i,M_{ij}) = \prod^{n,m}_{i=1,j=1}f(m_{ij})=\frac{1}{\sqrt{2\pi}}\exp\left(\frac{-\sum^n_{i=1}\sum^m_{j=1}(\hat{m}(K,R_i,t_i,M_{ij})-m_{ij})^2}{\sigma^2}\right)$
让L取得最大值，即让
$\sum^n_{i=1}\sum^m_{j=1} \| \hat{m}(K,R_i,t_i,M_{ij})-m_{ij} \|^2$
最小。这里使用的是多参数非线性系统优化问题的Levenberg-Marquardt算法进行迭代求最优解。

六、Levenburg-Marquardt算法

通常的最小二乘问题都可以表示为
$\min_x F(x) = \frac{1}{2}\sum_{i=1}^{n}(f_i(x)^2) = \frac{1}{2} \left \| f(x) \right \| ^2 = \frac{1}{2}f(x)^Tf(x)$
对 $f_i (x)$ 在 $x_k$ 处作泰勒展开
$f_i(x_k+h) \approx f_i(x_k)+\nabla f_i(x_k)^Th$
$f(x_k+h) \approx f(x_k)+J(x_k)h$
其中Jacobi矩阵
$J(x_k)=\begin{pmatrix} \nabla f_1(x_k)^T \\ \nabla f_2(x_k)^T \\ \vdots \\ \nabla f_n(x_k) \\ \end{pmatrix}= \begin{pmatrix} \frac{\partial f_1(x_k)}{\partial x_1} &\frac{\partial f_1(x_k)}{\partial x_2} &\cdots &\frac{\partial f_1(x_k)}{\partial x_m} \\ \frac{\partial f_2(x_k)}{\partial x_1} &\frac{\partial f_2(x_k)}{\partial x_2} &\cdots &\frac{\partial f_2(x_k)}{\partial x_m} \\ \vdots &\vdots &\ddots &\vdots \\ \frac{\partial f_n(x_k)}{\partial x_1} &\frac{\partial f_n(x_k)}{\partial x_2} &\cdots &\frac{\partial f_n(x_k)}{\partial x_m} \end{pmatrix}$
记 $f_k=f(x_k),J_k=J(x_k)$ 那么
$\frac{\partial F(x)}{\partial x_j} = \sum_{i=1}^{n}f_i(x)\frac{\partial f_i(x)}{\partial x_j}$
即F(x)的梯度
$g=F'(x)=J(x)^Tf(x)$
下面讨论利用数值最优化方法求解非线性最小二乘问题的过程。
最速下降法
假设 $h^TF'(x) < 0$ ，则h是F(x)下降方向，即对于任意足够小的 $\alpha>0$ ，都满足
$F(x+αh)<F(x)$
则
$\lim_{\alpha\to0}\frac{F(x)-F(x+\alpha h)}{\alpha \left \| h \right \|}=-\frac{1}{\left \| h \right \|}h^TF'(x)=-||F'(x)||\cos \theta$
其中为矢量h和F'(x)夹角，当 $\theta=\pi$ 时，下降最大。即 $h_{sd}=−F'(x)$ 是最快下降方向。
高斯-牛顿算法
选择h使得F(x)在 $x_k$ 附近二阶近似，则
$\begin{split} F(x_k+h) \approx L(h) & = \frac{1}{2}f(x_k+h)^Tf(x_k+h) \\ & = \frac{1}{2}f_k^Tf_k+h^TJ_k^Tf_k+\frac{1}{2}h^TJ_k^TJ_kh \\ & = F(x_k) + h^TJ_k^Tf_k+\frac{1}{2}h^TJ_k^TJ_kh \end{split}$
则
$\frac{\partial}{\partial h} F(x_k+h)= J_k^Tf_k+J_k^TJ_kh=0 \Rightarrow (J_k^TJ_k)h_{gn}=-J_k^Tf_k$
即
$\begin{cases} h_{gn}=-(J_k^TJ_k)^{-1}J_k^Tf_k\\ x_{k+1}=x_k+h_{gn} \end{cases}$
直到 $\left |F(x_{k+1})-F(x_k) \right|< \varepsilon$
高斯-牛顿法可以看做使用Hessian矩阵的最速下降法
$H=\begin{pmatrix} \frac{\partial ^2f}{\partial x_1\partial x_1} & \frac{\partial ^2f}{\partial x_1\partial x_2} & \dots&\frac{\partial ^2f}{\partial x_1\partial x_n} \\\ \frac{\partial ^2f}{\partial x_2\partial x_1} & \frac{\partial ^2f}{\partial x_2\partial x_2} & \dots&\frac{\partial ^2f}{\partial x_2\partial x_n}\\\ \vdots & \vdots & \ddots&\vdots\\ \frac{\partial ^2f}{\partial x_n\partial x_1} & \frac{\partial ^2f}{\partial x_n\partial x_2} & \dots&\frac{\partial ^2f}{\partial x_n\partial x_n} \end{pmatrix}$
即
$\begin{cases} ||x||_{\nabla^2f(x)}=x^T\nabla^2f(x)x\\\Delta_{nsd}\leftarrow \text{arg} \min_v (\nabla f(x)^Tv\mid ||v||<=1)\Delta_{nsd} \end{cases}\Rightarrow \Delta_{nsd}=H^{-1}\nabla f(x)$
LM算法
通常高斯牛顿法收敛较快，但是不稳定，且要求 $J^T J$ 非奇异。而梯度下降法稳定，但是收敛较慢。所以接下来我们介绍高斯牛顿算法和最速下降法混合法，即Levenburg-Marquardt算法，即加入正则项使得 $(J_k^TJ_k+\lambda I)h=-J_k^Tf_k$
记其解为 $h_{lm}$ ，则
- $\lambda=0 \Rightarrow h_{lm}\approx h_{gn}$ ，即为Gauss-Newton法
- 当 $\lambda$ 充分大时 $\lambda Ih_{lm}\approx -J_k^Tf_k, h_{lm}=-\frac{1}{u}J_k^Tf_k$ ，即为最速下降法
- 特别当 $\lambda \rightarrow \infty, ||h_{lm} || \rightarrow 0$
因为
$\begin{split} F(x+h) \approx L(h) & = \frac{1}{2}f(x+h)^Tf(x+h) \\ & = \frac{1}{2}f^Tf+h^TJ^Tf+\frac{1}{2}h^TJ^TJh \\ & = F(x) + h^TJ^Tf+\frac{1}{2}h^TJ^TJh \end{split}$
所以定义增益比 $\rho=\frac{F(x)-F(x+h_{lm})}{L(0)-L(h_{lm})}$ 则

- 在实际中，我们选择一阶近似、二阶近似并不是在所有定义域都满足的，而是在 $|x-x_0|<\varepsilon$ 作用域内满足这个近似条件。
- 当 $\rho$ 较大时，表明F(x+h)的二阶近似L(h)比F(x+h)更加接近于F(x)，因此二阶近似比较好，所以可以减小 $\lambda$ ，采用更大的迭代步长，接近Gauss-Newton法来更快收敛；
- 当 $\rho$ 较小时，表明采取的二阶近似较差，因此通过增大 $\lambda$ ，采用更小的步长，接近最速下降法来稳定的迭代。

LM算法伪代码

总结：张正友平面标定法伪代码

张氏标定法伪代码

转自：https://zhuanlan.zhihu.com/p/36371959