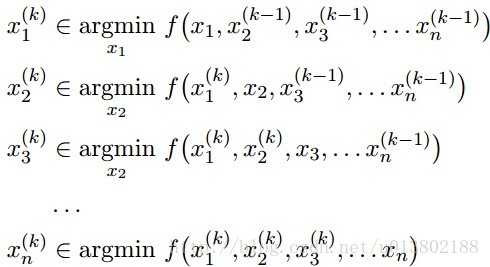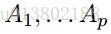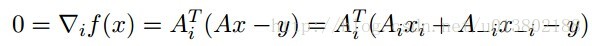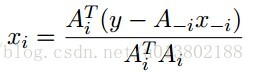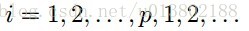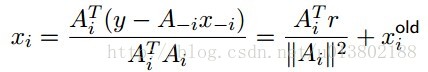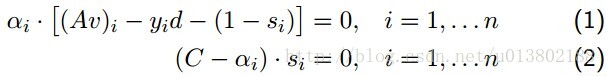坐标下降和块坐标下降法

坐标下降法（英语：coordinate descent）是一种非梯度优化算法。算法在每次迭代中，在当前点处沿一个坐标方向进行一维搜索以求得一个函数的局部极小值。在整个过程中循环使用不同的坐标方向。对于不可拆分的函数而言，算法可能无法在较小的迭代步数中求得最优解。为了加速收敛，可以采用一个适当的坐标系，例如通过主成分分析获得一个坐标间尽可能不相互关联的新坐标系（参考自适应坐标下降法）。

坐标下降优化方法为了找到一个函数的局部极小值，在每次迭代中可以在当前点处沿一个坐标方向进行一维搜索。在整个过程中循环使用不同的坐标方向。一个周期的一维搜索迭代过程相当于一个梯度迭代。其实，gradient descent 方法是利用目标函数的导数（梯度）来确定搜索方向的，而该梯度方向可能不与任何坐标轴平行。而coordinate descent方法是利用当前坐标系统进行搜索，不需要求目标函数的导数，只按照某一坐标方向进行搜索最小值。坐标下降法在稀疏矩阵上的计算速度非常快，同时也是Lasso回归最快的解法。

算法描述

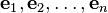坐标下降法基于的思想是多变量函数 $F(\mathbf{x})$ 可以通过每次沿一个方向优化来获取最小值。与通过梯度获取最速下降的方向不同，在坐标下降法中，优化方向从算法一开始就予以固定。例如，可以选择线性空间的一组基 $\mathbf{e}_1, \mathbf{e}_2, \dots, \mathbf{e}_n$ 作为搜索方向。在算法中，循环最小化各个坐标方向上的目标函数值。亦即，如果 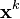$\mathbf{x}^k$ 已给定，那么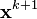， $\mathbf{x}^{k+1}$ 的第 $i$ 个维度为

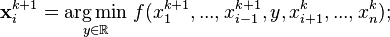
$\mathbf{x}^{k+1}_i = \underset{y\in\mathbb R}{\operatorname{arg\,min}}\; f(x^{k+1}_1,...,x^{k+1}_{i-1},y,x^k_{i+1},...,x^k_n);$

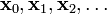因而，从一个初始的猜测值 $\mathbf{x}_0$ 以求得函数 $F$ 的局部最优值，可以迭代获得 $\mathbf{x}_0, \mathbf{x}_1, \mathbf{x}_2, \dots$ 的序列。

通过在每一次迭代中采用一维搜索，可以很自然地获得不等式

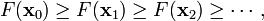
$F(\mathbf{x}_0)\ge F(\mathbf{x}_1)\ge F(\mathbf{x}_2)\ge \cdots,$

可以知道，这一序列与最速下降具有类似的收敛性质。如果在某次迭代中，函数得不到优化，说明一个驻点已经达到。

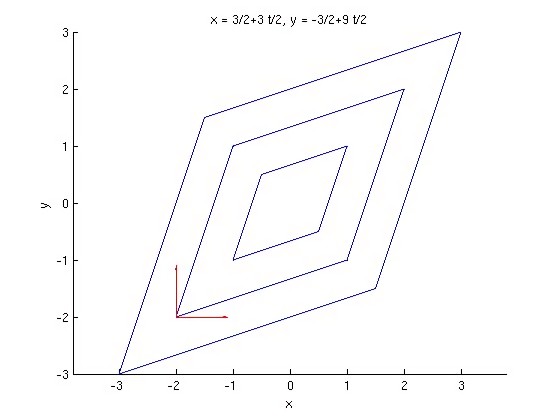
这一过程可以用下图表示。

例子

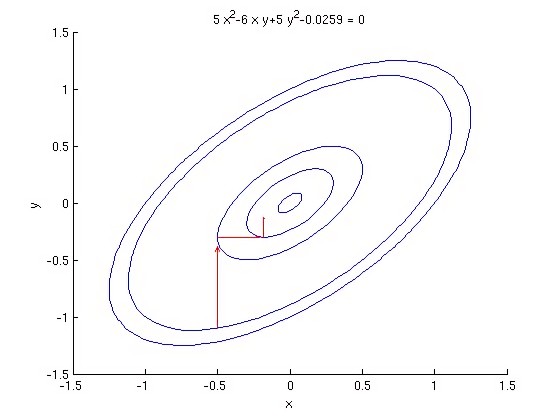
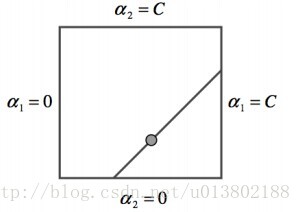
对于非平滑函数，坐标下降法可能会遇到问题。下图展示了当函数等高线非平滑时，算法可能在非驻点中断执行。

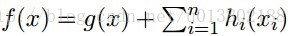
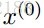
对所有的，其中g是可微的凸函数，每一个hi都是凸的，我们可以使用坐标下降寻求一个最小值，我们从一个最初的猜想开始，对k进行循环：

每一次我们解决了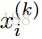，我们都会使用新的值。

Tseng (2001)的开创性工作证明：对这种f（f在紧集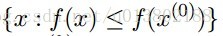上连续，且f到达了其最小值），的极限值，k=1,2,3….是f的一个最小元(minimizer)。

在实分析领域：

随后收敛与x*( Bolzano-Weierstrass)

收敛于f*( monotoneconvergence)

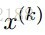
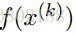
其中：

坐标下降的顺序是任意的，可以是从1到n的任意排列。

可以在任何地方将单个的坐标替代成坐标块

关键在于一次一个地更新，所有的一起更新有可能会导致不收敛

我们现在讨论一下坐标下降的应用：

线性回归：

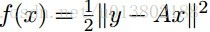
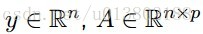
令，其中，A有p列：

最小化xi，对所有的xj，j不等于i：

解得：

坐标下降重复这个更新对所有的

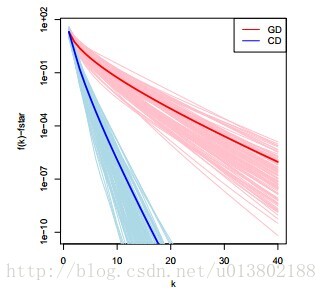
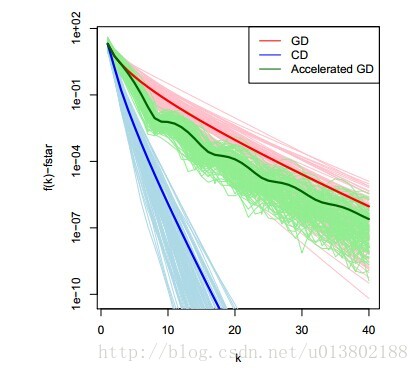
对比坐标下降与梯度下降在线性回归中的表现（100个实例，n=100，p=20）

将坐标下降的一圈与梯度下降的一次迭代对比是不是公平呢？是的。

其中r=y-Ax。每一次的坐标更新需要O(n)个操作，其中O(n)去更新r，O(n)去计算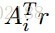，所以一圈就需要O(np)，跟梯度下降是一样的。

我们用相同的例子，用梯度下降进行比较，似乎是与计算梯度下降的最优性相违背。

那么坐标下降是一个一阶的方法吗？事实上不是，它使用了比一阶更多的信息。

现在我们再关注一下支持向量机：

SVM对偶中的坐标下降策略：

SMO(Sequentialminimal optimization)算法是两块的坐标下降，使用贪心法选择下一块，而不是用循环。

回调互补松弛条件(complementaryslackness conditions)：

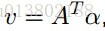
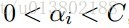
v，d，s是原始的系数，截距和松弛，其中，使用任何的（1）中i使得来计算d，利用（1）（2）来计算2.

SMO重复下面两步：

选出不满足互补松弛的αi，αj

最小化 αi，αj使所有的变量满足条件

第一步使用启发式的方法贪心得寻找αi，αj，第二步使用等式约束。

Group Lasso

Yuan在2006年将lasso方法推广到group上面，诞生了group lasso。我们可以将所有变量分组，然后在目标函数中惩罚每一组的L2范数，这样达到的效果就是可以将一整组的系数同时消成零，即抹掉一整组的变量，这种手法叫做Group Lasso 分组最小角回归算法。其目标函数为：

minβ(||Y−Xβ||22+λ∑g=1G||ql−−√βIg||2)minβ(||Y−Xβ||22+λ∑g=1G||qlβIg||2)

在group lasso中，将p个特征分成G组，其中i的取值为1，2..g.. G。IgIg是g组的特征下标， ql−−√ql是每一组的加权，可以按需调节。不同于Lasso 方法将每个特征的系数项的绝对值加总，这里所加总的是每个组系数的 L2 范数，在优化的过程中，该结构尽量选出更少的组（组间稀疏），而组内是L2范数，稀疏约束没那么强。

容易看出，group lasso是对lasso的一种推广，即将特征分组后的lasso。显然，如果每个组的特征个数都是1，则group lasso就回归到原始的lasso。为了求解group lasso，可以首先假设组内特征是正交的，针对这种情形可以利用分块坐标下降法求解，对于非正交的情形，可以首先对组内特征施加正交化。

Group Lasso 可以应用块坐标下降法来求解(BCD)，算法框架如下：

具体内容参考http://www.math.ucla.edu/~wotaoyin/papers/bcu/