什么是时间序列
简而言之:
对某一个或者一组变量x(t)进行观察测量,将在一系列时刻t1,t2,⋯,tn所得到的离散数字组成的序列集合,称之为时间序列。
例如: 某股票A从2015年6月1日到2016年6月1日之间各个交易日的收盘价,可以构成一个时间序列;某地每天的最高气温可以构成一个时间序列。
一些特征:
趋势:是时间序列在长时期内呈现出来的持续向上或持续向下的变动。
季节变动:是时间序列在一年内重复出现的周期性波动。它是诸如气候条件、生产条件、节假日或人们的风俗习惯等各种因素影响的结果。
循环波动:是时间序列呈现出得非固定长度的周期性变动。循环波动的周期可能会持续一段时间,但与趋势不同,它不是朝着单一方向的持续变动,而是涨落相同的交替波动。
不规则波动:是时间序列中除去趋势、季节变动和周期波动之后的随机波动。不规则波动通常总是夹杂在时间序列中,致使时间序列产生一种波浪形或震荡式的变动。只含有随机波动的序列也称为平稳序列。
平稳性
在百度词条中是这样粗略的讲的:平稳时间序列粗略地讲,一个时间序列,如果均值没有系统的变化(无趋势)、方差没有系统变化,且严格消除了周期性变化,就称之是平稳的。
我们不妨先来看下图:
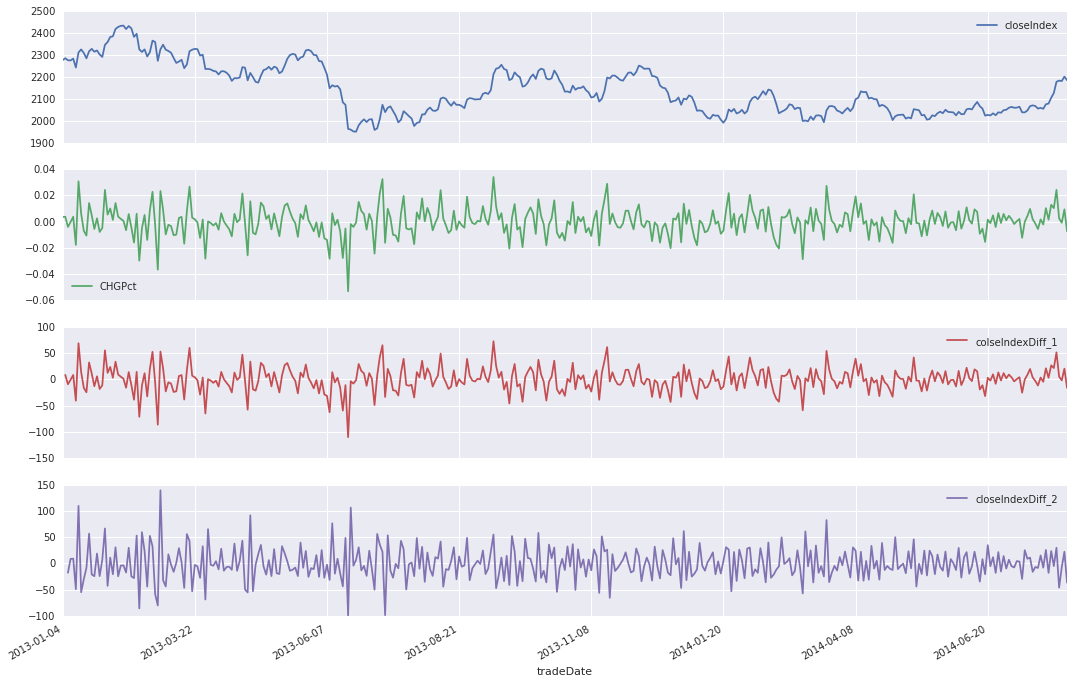
上图中第一张图为上证综指部分年份的收盘指数,是一个非平稳时间序列;而下面两张为平稳时间序列(当然这里没有检验,只是为了让大家看出差异,关于检验序列的平稳性后续会讨论)
细心的朋友已经发现,下面两张图,实际上是对第一个序列做了差分处理,方差和均值基本平稳,成为了平稳时间序列,后面我们会谈到这种处理。
下面可以给出平稳性的定义了:
严平稳:
如果对所有的时刻t,任意正整数k和任意k个正整数
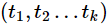
,
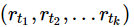
的联合分布与
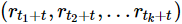
的联合分布相同,我们称时间序列{rt}是严平稳的。
也就是,
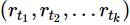
的联合分布在时间的平移变换下保持不变,这是个很强的条件。而我们经常假定的是平稳性的一个较弱的方式
弱平稳:
若时间序列{rt}满足下面两个条件:
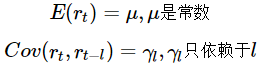
则时间序列{rt}为弱平稳的。即该序列的均值,**rt与rt−l的协方差不随时间而改变,l为任意整数。
在金融数据中,通常我们所说的平稳序列,是弱平稳的。**
差分
回头我们再谈之前说的差分操作:
差分(这里为前向),就是求时间序列{rt}在t时刻的值rt与t−1时刻的值rt−1的差不妨记做dt,则我们得到了一个新序列{dt},为一阶差分,对新序列{dt}再做同样的操作,则为二阶差分。
假设y表示t时刻的Y的差分:
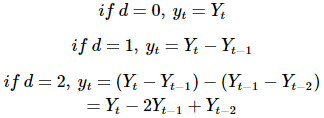
通常非平稳序列可以经过d次差分,处理成弱平稳或者近似弱平稳时间序列。回头看上图,我们发现二阶差分得到的序列比一阶差分效果更好。
相关系数和自相关函数
相关系数
对于两个向量,我们希望定义它们是不是相关。一个很自然的想法,用向量与向量的夹角来作为距离的定义,夹角小,就距离小,夹角大,就距离大。
早在中学数学中,我们就经常使用余弦公式来计算角度:
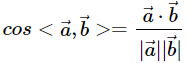
而对于a⃗ ⋅b⃗ 我们叫做内积,例如

我们再来看相关系数的定义公式,X和Y的相关系数为:

而我们的根据样本的估计计算公式为:
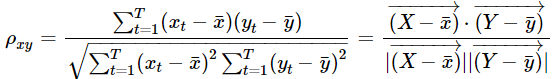
我们发现,相关系数实际上就是计算了向量空间中两个向量的夹角! 协方差是去均值后两个向量的内积!
如果两个向量平行,相关系数等于1或者-1,同向的时候是1,反向的时候就是-1。如果两个向量垂直,则夹角的余弦就等于0,说明二者不相关。两个向量夹角越小,相关系数绝对值越接近1,相关性越高。 只不过这里计算的时候对向量做了去均值处理,即中心化操作。而不是直接用向量X,Y计算。
对于减去均值操作,并不影响角度计算,是一种“平移”效果,如下图所示:

自相关函数 (Autocorrelation Function, ACF)
相关系数度量了两个向量的线性相关性,而在平稳时间序列{rt}中,我们有时候很想知道,rt与它的过去值rt−i的线性相关性。 这时候我们把相关系数的概念推广到自相关系数。
rt与rt−l的相关系数称为rt的间隔为l的自相关系数,通常记为ρl。具体的:
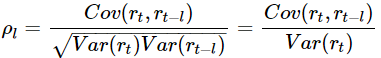
这里用到了弱平稳序列的性质:
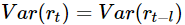
对一个平稳时间序列的样本{rt},1≤t≤T,则间隔为l的样本自相关系数的估计为:
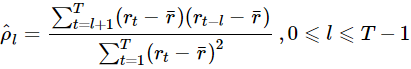
则函数
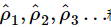
称为rt的样本自相关函数(ACF)
当自相关函数中所有的值都为0时,我们认为该序列是完全不相关的;因此,我们经常需要检验多个自相关系数是否为0。
混成检验
原假设 H0:ρ1=…=ρm=0
备择假设 H1:∃i∈1,…,m,ρi≠0
混成检验统计量:
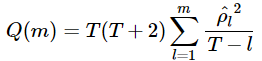
Q(m)渐进服从自由度为m的χ2分布
决策规则:
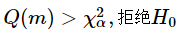
即,Q(m)的值大于自由度为m的卡方分布100(1−α)分位点时,我们拒绝H0。
大部分软件会给出Q(m)的p-value,则当p-value小于等于显著性水平α时拒绝H0。
白噪声序列和线性时间序列
白噪声序列
随机变量X(t)(t=1,2,3……),如果是由一个不相关的随机变量的序列构成的,即对于所有S不等于T,随机变量Xt和Xs的协方差为零,则称其为纯随机过程。
对于一个纯随机过程来说,若其期望和方差均为常数,则称之为白噪声过程。白噪声过程的样本实称成为白噪声序列,简称白噪声。之所以称为白噪声,是因为他和白光的特性类似,白光的光谱在各个频率上有相同的强度,白噪声的谱密度在各个频率上的值相同。
线性时间序列
时间序列{rt},如果能写成:

则我们称{rt} 为线性序列。其中at称为在t时刻的新息(innovation)或扰动(shock)
很多时间序列具有线性性,即是线性时间序列,相应的有很多线性时间序列模型,例如接下来要介绍的AR、MA、ARMA,都是线性模型,但并不是所有的金融时间序列都是线性的
对于弱平稳序列,我们利用白噪声的性质很容易得到rt的均值和方差:

因为Var(rt)一定小于正无穷,因此ψ2i必须是收敛序列,因此满足

即,随着i的增大,远处的扰动at−i对rt的影响会逐渐消失。
到目前为止介绍了一些基本知识和概念,如平稳性、相关性、白噪声、线性序列,介绍的过程中并没有太深入,目前来说“够用”了,一些细节会在后面章节补充。下面开始介绍一些线性模型。
参考:https://uqer.io/v3/community/share/5790a091228e5b90cda2e2ea