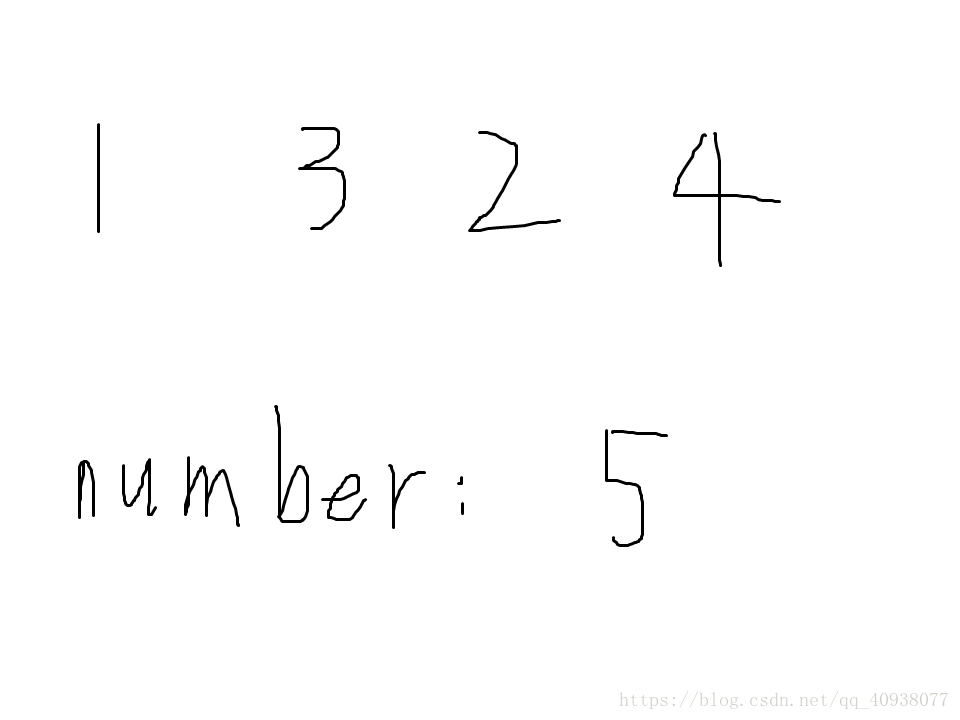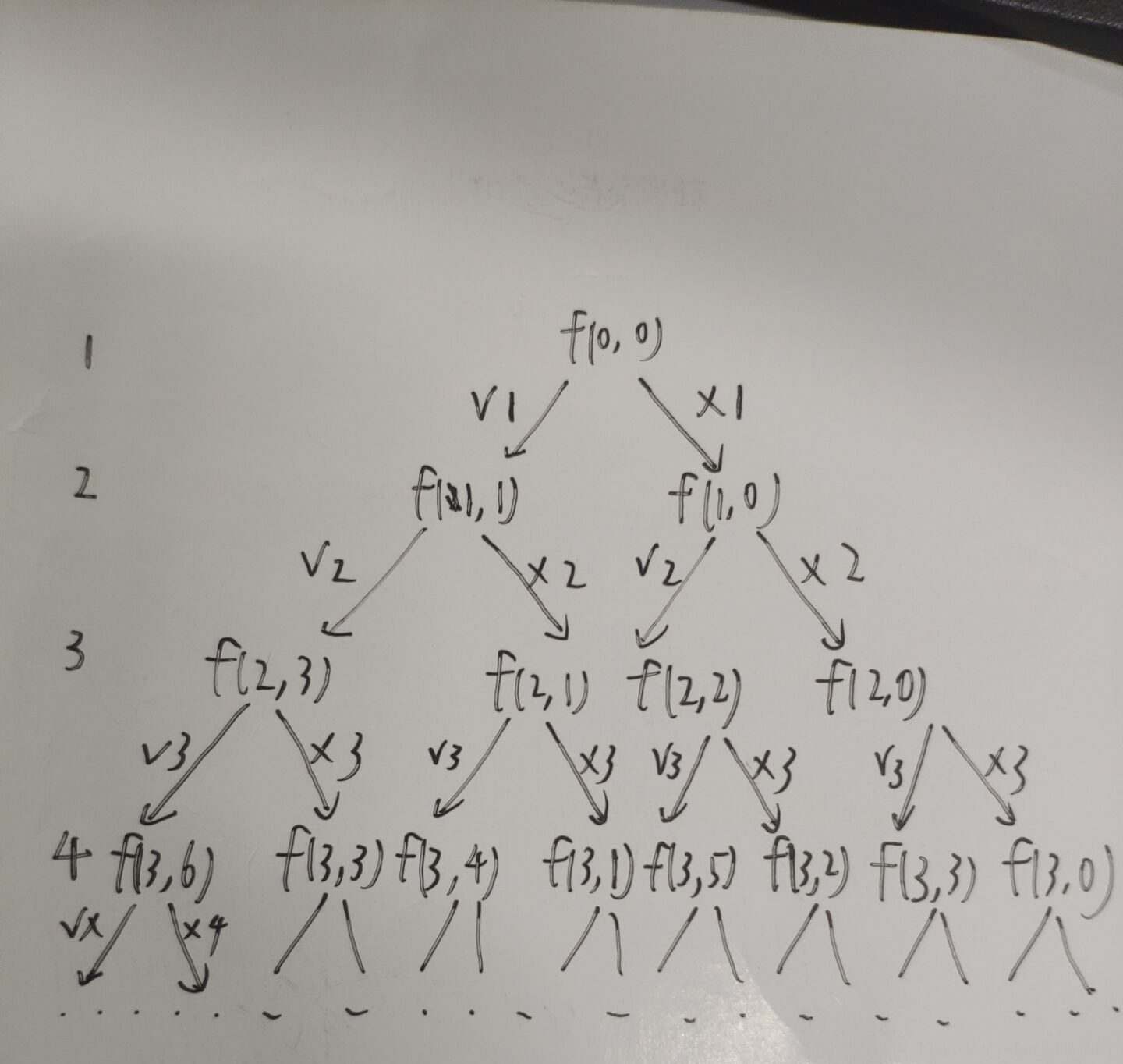题目一:
题意:
给定一个地图,每个位置上都有权值,你从地图的左上角开始走,走到右下角,让你找出所有路径中权值和最小的 一条路。
题目分析:
我们假顶walk( i , j )函数所代表的意思是地图上( i , j )这个点到右下角的最短距离,那么我们就可以写递归函数了,直接看代码
代码如下:
#include<bits/stdc++.h>
#define MAXN 99999
using namespace std;
int n,m;
int root[MAXN];
int walk(int i,int j)
{
if(i==n&&j==m)//如果到了右下角,那么问题就变成了右下角的点到右下角的点的最短距离,肯定是root[i][j]本身
return root[i][j];
if(i==n)//到了地图的最后一行,只能往右边走了
return walk(i,j+1)+root[i][j];
if(j==m)//到了地图的最右边一列,只能往下走了
return walk(i+1,j)+root[i][j];
return min(walk(i+1,j),walk(i,j+1))+root[i][j];//一般情况,往下走的最短路径和往右走的最短路径中找出最小的加上root[i][j]就是当前的结果
}
分析如何该成动态规划:
改成动态规划的步骤:
第一步:找到递归函数变化的形参,作为数组的维度。形参的变化范围就是数组维度上的大小
第二步:通过题目和我们设定的递归函数所表达的意思来找出我们需要的表中的哪个位置。从递归函数中找出递归出口(不用计算就可以得到的位置),这就是dp表中的初值位置
第三步:分析递归函数一般情况依赖于哪些情况,从而能够确定动归中表的遍历顺序
这样说可能很抽象,对着题目来分析:
举个实例:
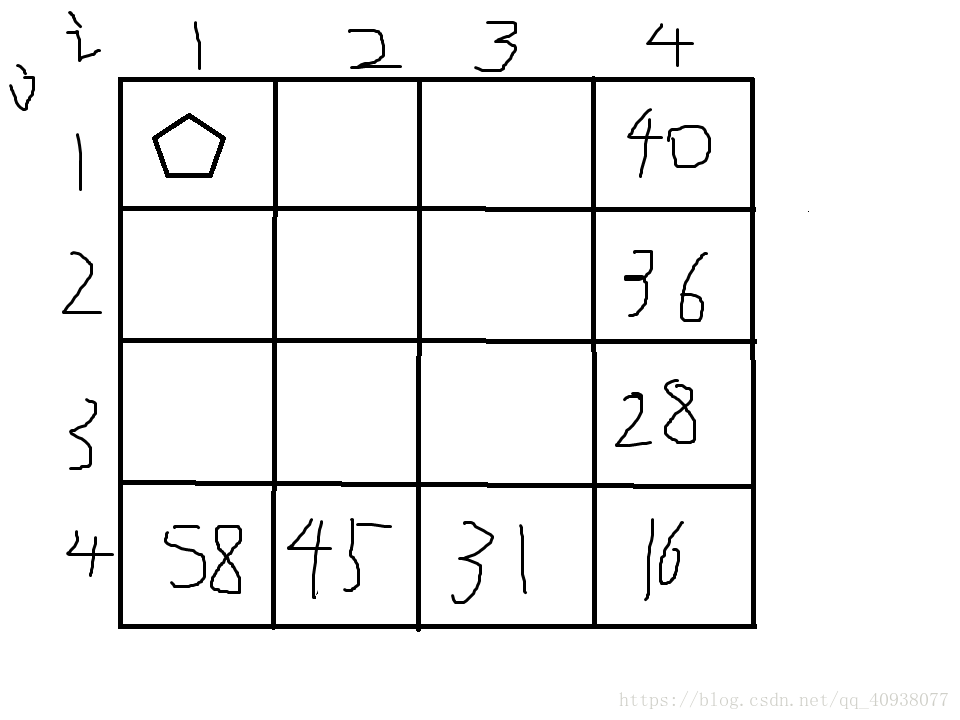
第一步:从递归函数来看,i,j为变化的参数,那么就建立一个二维数组(dp表),横坐标的大小就是i的变化范围,纵坐标的大小就是j的变化范围。
第二步:通过题目和我们设定的递归函数的意思,可以得到我们需要dp表中的(1,1)位置,初始位置通过递归函数的递归出口可以找到,下图中都已经标出来了。
第三步:通过分析递归函数可得,dp表中任意一个普遍位置依赖于它的右边的位置和下边的位置,从而可以得出遍历表的顺序是从右到左,从下到上的顺序,看下图。
至此,我们就能够写出动归版本的代码了
代码如下:
void dpwalk()
{
memset(visited,sizeof(visited),0);//初始化dp表
visited[n][m]=root[n][m];
for(int i=n-1;i>=1;i--)
visited[i][m]=visited[i+1][m]+root[i][m];
for(int j=m-1;j>=1;j--)
visited[n][j]=visited[n][j+1]+root[n][j];
for(int i=n-1;i>=1;i--)//以从下到上,从右到左的顺序填充dp表
for(int j=m-1;j>=1;j--)
visited[i][j]=min(visited[i+1][j],visited[i][j+1])+root[i][j];
cout<<visited[1][1]<<endl;//输出所需要的dp表中的位置
}
题目二:
题意:
给你一串数字和一个给定的数字number,问你可不可以通过那一串数字中的任意数字相加来凑出number,如果可以,返回true,否则,返回false。
题目分析:
对于每个数字,我们有两种选择,第一个是加上这个数字,第二个是不加这个数字。我们可以设定一个函数issum(nowdaysum,i)代表选到第i个数字时的和为nowdaysum。
代码如下:
#include<bits/stdc++.h>
#define MAXN 99999
using namespace std;
int root[MAXN];
int n;
bool issum(int nowdaysum,int i)
{
if(i==n)//如果已经到了最后一个数字,判断一下决定返回true还是false
return nowdaysum==number;
return (issum(nowday+root[i],i+1)||issum(nowday,i+1));//选当前数字和不选当前数字中只要有一个能够凑出number来,就返回true
}
改成动归版本:
还是按照上面说的那几个步骤来:
一:从递归函数来看,nowdaysum和i是变化的,所以建立一个二维的dp表,横坐标的变化范围就是nowdaysum的变化范围
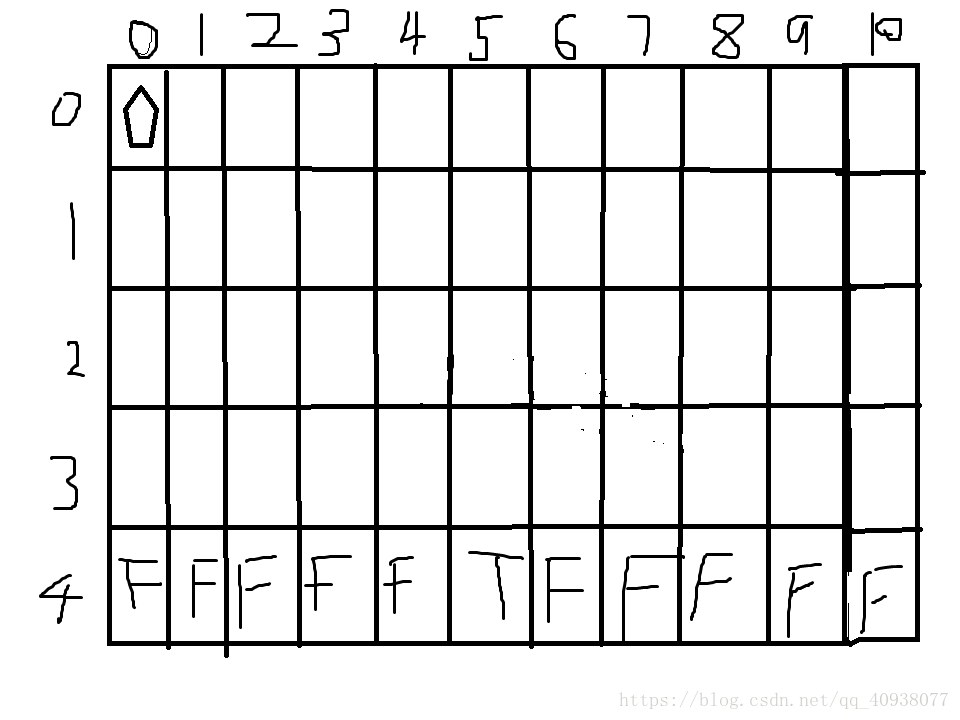
二:通过分析递归函数的出口,可以得知dp表的最后一行第number列是可以直接知道的。我们需要的是dp表中(0,0)位置上的值。
三:通过分析递归函数可以知道,普遍位置需要的是其同列下一行的位置和其下一行右边的位置(具体位置是下一行的当前列数加上root[i]列),可以得到填充dp表的顺序是从下到上,从右到左。
至此,我们可以写出dp版本的程序了。
代码如下:
int main()
{
memset(visited,0,sizeof(visited));
visited[n][number]=true;
for(int i=n-1;i>=0;i--)
for(int j=sum;j>=0;j--)
if(j+root[i]<=sum)//确保不越界
visited[i][j]=visited[i+1][j]||visited[i+1][j+root[i]];//只要有一个可以凑出number来,说明这个状态就可以凑出number来
cout<<visited[0][0]<<endl;
}
接下来分析一下这些题目为何能够从暴力递归转化成动态规划:
首先看第一题:
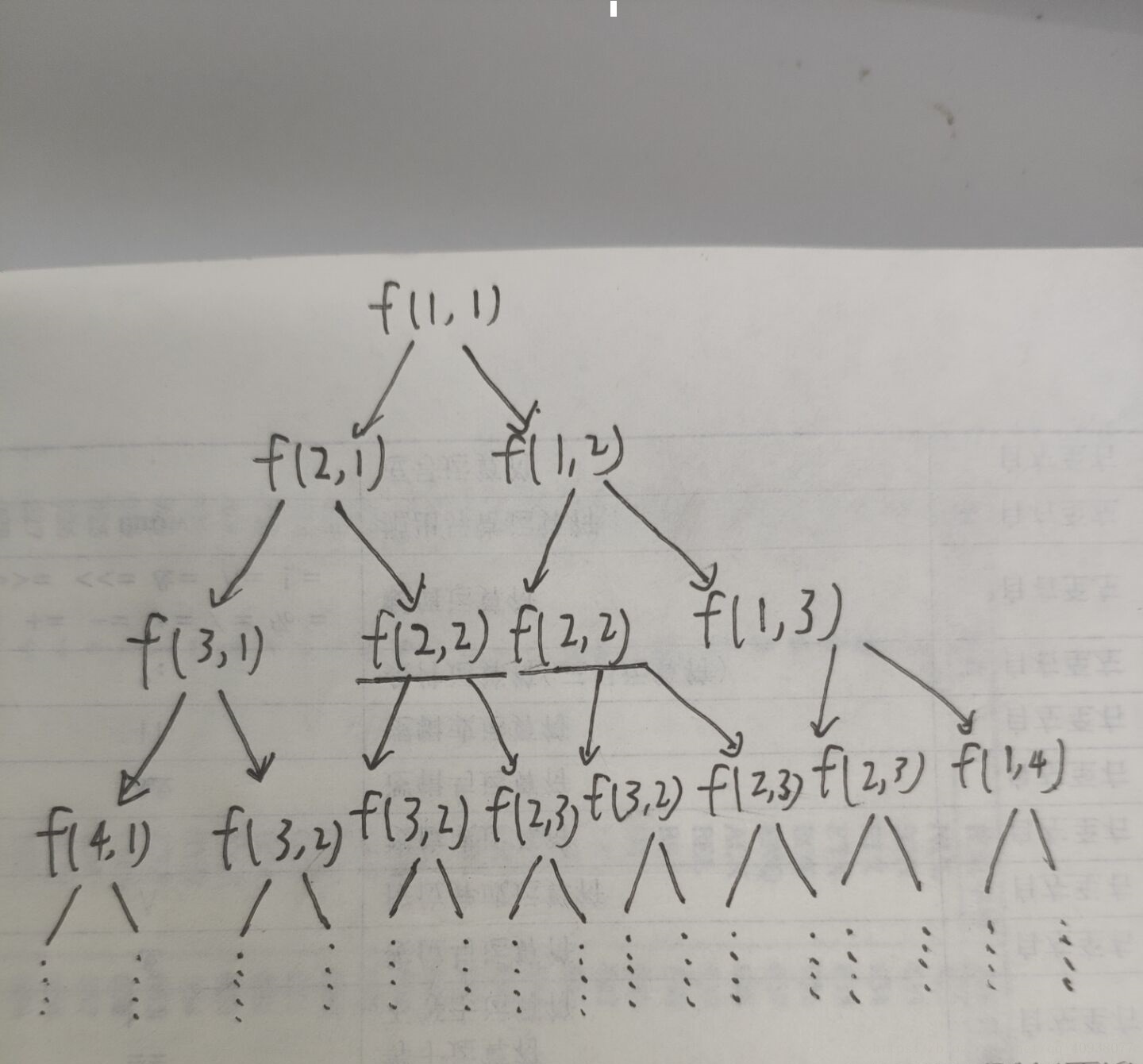
暴力递归版本所经过的状态:
从图中可以看出,(一)暴力递归版本有很多的重复计算,比如:f(2,2)、f(2,3)等等,这样很浪费时间,所以人们才想出了通过空间换取时间的动态规划的方法。如果一个暴力递归的代码可以改成动态规划,那么它一定满足一个条件,(二)那就是无后效性,啥意思呢?看这个问题,f(2,2)代表的是从地图(2,2)这个点到达地图右下角的最短路径是多少,f(2,2)这个状态的返回值是固定的,与如何来到地图上(2,2)这个点是没有关系的(无论是从(1,2)这个点来(2,2)还是从(2,1)这个点来(2,2),f(2,2)这个状态的返回值都是固定的)。只要你这个状态的参数一定,那么这个状态的返回值就是一定的。
只有你写出的暴力递归版本同时满足上面两个条件,才可以改成动态规划版本。
接下来看第二题:
还是分析暴力递归版本的经过的状态:
通过图中还是可以看出有很多的重复计算,并且可以分析得到,任何一个状态只要是参数确定了,它的返回值就一定是确定的。(看上面的f(3,3)这个状态,这个状态可以由两个状态:f(2,3)和f(2,0)这两个状态转移过来,但是你只要到了f(3,3)这个状态了,它的返回值就是确定的了)
满足了无后效性。所以可以改成动态规划版本。