暴力递归转动态规划（一）

前两篇帖子介绍了暴力递归的过程，总的来说就是利用自然智慧+不断的尝试。这篇文章则会介绍如何将暴力递归转成动态规划。

斐波那契数列
斐波那契数列一定都不陌生，规定第一列的值是1，第二列的值是2的话，那第七列的值就是13，以此类推，整体上是一个 f(N) = f(N -1 ) + f(N - 2)。

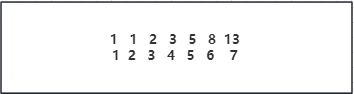
那如果尝试着用暴力递归的思想来解决的话代码如下：

public static int f(int N) {
    
    
        if (N == 1) {
    
    
            return 1;
        }
        if (N == 2) {
    
    
            return 1;
        }
        return f(N - 1) + f(N - 2);
    }

这么简短的几行代码其实就实现了斐波那契数列数列，那如果此时要求f(7)的值，展开来看的话，其实是不是就是一个二叉树的形状。f(7)依赖着f(5)、f(6)。f(6)依赖着f(5)、f(4)以此类推。。。。

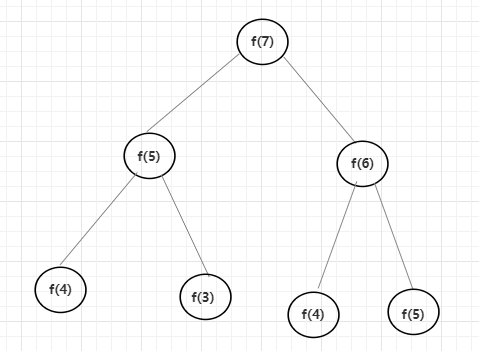
通过画图可以看出，想要求出一个f(7)的值，会依赖很多方法，而且有的方法会执行很多次，那如果此时有一张表结构，可以将之前的结果 “缓存” 起来，以后碰到了直接拿值。是不是就方便了很多，用$O(N)$的时间复杂度就可以解决这个问题。
这个"缓存"，就是动态规划。来一道具体的题目巩固一下：

题目
假设有排成一行的N个位置，记为1 ~ N，N >= 2 , 有一个机器人，
开始时，机器人在其中的start位置（start是1 ~ N 中间的一个）。
如果机器人当前在1位置，那下一步只能向右来到2的位置。
如果机器人在N位置，那下一步只能向左来到 N - 1位置。
如果在中间，则可以左右挪动。规定机器人必须走K步，最终来到target位置，（target也是1 ~ N中的一个）。
问机器人从start必须走K步，来到target位置，一共有多少种方法。

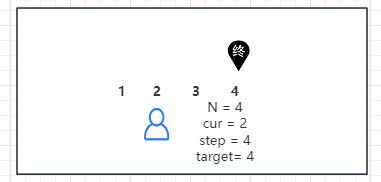
如果所示，假设当前起点在2，终点在4，共4个位置，一共走4步，共有几种方法可以走到：共三种

1. 2 -> 1 -> 2 - >3 -> 4
2. 2 -> 3 -> 4 -> 3 -> 4
3. 2 -> 3 -> 2 -> 3 -> 4

暴力递归

1. 根据题目分析，确认base case ，当step 为0，说明没有步数可以走， 就return。
2. 如果cur = 1，那下一步只能向右走。
3. 如果cur = N，那下一步只能向左走。
4. 否则，在中间，则左右都可以，那向左走到达target的方法 + 向右走到达target的方法，就是总共的方法数。

代码
参数cur：当前机器人所在位置 step：剩余的步数 target：目标位置 N：一共N个位置
K：一共有多少步

 	//方法返回机器人从cur出发，走step步，到达target的方法数
    public static int ways(int cur, int K, int target, int N) {
    
    
        return process(cur, K, target, N);
    }

    public static int process(int cur, int step,int target, int N) {
    
    
    	//当步数为0时，看当前位置是否在目标位置，如果在，则方法数 + 1，否则认为没走到为0
        if (step == 0) {
    
    
            return cur == target ? 1 : 0;
        }
        //无论怎么走，每走一步 step 一定 -1
		//当前位置为1时，必须向右，所以下一步会是在2位置
        if (cur == 1) {
    
    
            return process(2, step - 1, target, N);
        }
        //当前位置为N时，必须向左，所以下一步在N -1位置
        if (cur == N) {
    
    
            return process(N - 1, step - 1, target, N);
        }
        //否则，在中间，可能向左走，也可能向右走
        return process(cur + 1, step - 1, target, N) + process(cur - 1, step - 1, target, N);
    }

优化
如何利用暴力递归优化成动态规划其中很重要的一点就是，根据调用过程，看有没有重复接，如果出现重复解的情况，则一定可以优化成动态规划。
从上面的代码中可以分析出，影响ways方法结果的因素都有什么？
N是固定不变的，target也是固定不变的，而上面的代码中，是不是只有cur当前位置的变化以及step在不停的减少。所以，影响整个结果的参数是当前位置和步数。
将过程展开来看。比如说现在start = 7, target = 15，step = 10，从7位置出发走到15位置，要走10步，看看它都有什么走法。

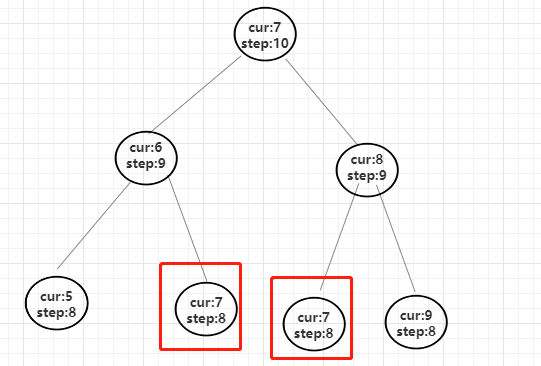
7是中间位置，出发后，左右两边都可以走，当走到当前位置为7时，剩余步数是8，子过程有重复调用情况，说明可以由暴力递归优化成动态规划。此时不用在意之前的调用情况。
因为此时两个画圈地方的当前位置都是7，剩余步数是8，以及target是15是固定不变的，所以此时到target的方法数一定是一样的。所以不用在意是 7 -> 6 -> 7 还是 7- > 8 -> 7。
由此可以分析出，cur和step是决定状态的key，只要这两个确定了，那结果就可以确定了。
找到了key，根据key创建一个二维数组，来代表缓存的表。如果来到当前位置，并且剩余步数还一样，那到达target的方法数也一定相同，如果缓存表中存在，可直接通过缓存表获取即可。

代码

	//cur范围：0 ~ N
    //step范围：0 ~ K
    public static int ways2(int cur, int K, int target, int N) {
    
    
        //创建一个N + 1和 K + 1返回的数组，保证到任何位置都能囊括进去
        int[][] dp = new int[N + 1][K + 1];
        for (int i = 0; i <= N; i++) {
    
    
            for (int j = 0; j <= K; j++) {
    
    
                dp[i][j] = -1;
            }
        }
        return process2(cur, K, target, N, dp);
    }

    public static int process2(int cur, int step, int target, int N, int[][] dp) {
    
    
        //不等于 -1 说明 之前计算过当来到cur位置时，剩余step 到达target的方法数
        if (dp[cur][step] != -1) {
    
    
            return dp[cur][step];
        }
        //走到这，说明没算过
        int ans = 0;
        if (step == 0) {
    
    
            ans = cur == target ? 1 : 0;
        } else if (cur == 1) {
    
    
            ans = process2(2, step - 1, target, N, dp);
        } else if (cur == N) {
    
    
            ans = process2(N - 1, step - 1, target, N, dp);
        } else {
    
    
            ans = process2(cur + 1, step - 1, target, N, dp) + process2(cur - 1, step - 1, target, N, dp);
        }
        //记录当前位置到达target的方法数。
        dp[cur][step] = ans;
        return ans;
    }

此时，代码已经经历了"傻缓存"的优化，通过dp表来记录每一步的方法数，这种从顶向下的动态规划，名字叫做"记忆化搜索"，本质上走每一个分支就是搜索，通过缓存表形成记忆化，利用空间换时间，通过一张缓存表来换取更大的时间。

如何将上面代码进行再次的优化？
上面通过cur当前所在位置以及剩余步数step构建了一个二维数组的缓存表，这个二维数组包含了给定的cur和step内每一步所有结果，那是不是可以尝试将这个dp表画出来？假设，当前机器人在2位置，总共5个位置，要走6步，目标是走到位置4。
所以cur = 2 K = 6 N =5 target = 4 ，画出来的图是这样的。

其中行是当前所在位置，列是步数，因为不可能到达0行，所以0行所在位置标记x。初始位置是2，还剩6步，标星星。
我只要将图补全，将当前位置和每一步的结果方法数填充到格子中。是不是就可以直接从表中知道2-6位置的步数。

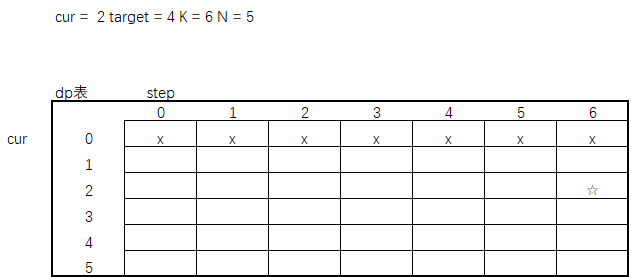
那该如何完善这个表么？从最开始的暴力递归代码做起，有一些base case会直接给我们答案。根据代码逻辑一行一行的完善。

 public static int process(int cur, int step, int target, int N) {
    
    
        if (step == 0) {
    
    
            return cur == target ? 1 : 0;
        }

        if (cur == 1) {
    
    
            return process(2, step - 1, target, N);
        }
        if (cur == N) {
    
    
            return process(N - 1, step - 1, target, N);
        }
        return process(cur + 1, step - 1, target, N) + process(cur - 1, step - 1, target, N);
    }

先从base case来，如果我剩余步数为0，此时如果 cur 的位置在 target 上的话，是不是说明有一种方法是可以到达的，其余不在target位置上方法数就是0，所以第一列就出来了。

继续接着往下看，当前是cur、step的状态（参数传进来的）那如果当前位置 cur = 1，根据题意，下一步只能向2位置挪动，而每移动一次step - 1，所以如果此时是cur = 1,step = 1的情况下，依赖的是cur = 2，step = 0的结果。所以cur在第一行任意位置依赖关系是这样的。

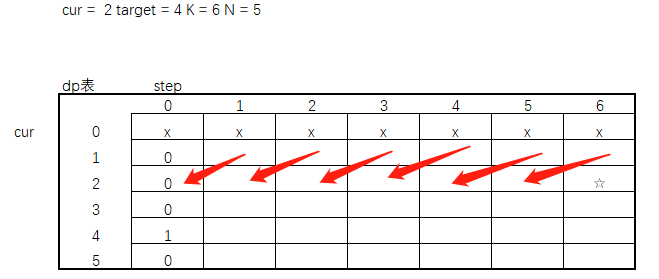
继续往下，如果当前cur = N，那下一步只能向左移动（N -1），同样每移动一次step - 1，所以cur在N行任意位置的依赖关系是这样的。

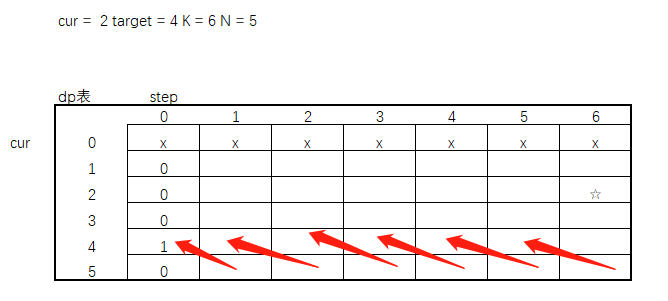
好，现在只剩普遍位置了，假设此时 cur = 3，看代码，可以左移也可以右移。所以此时的依赖关系是这样的。

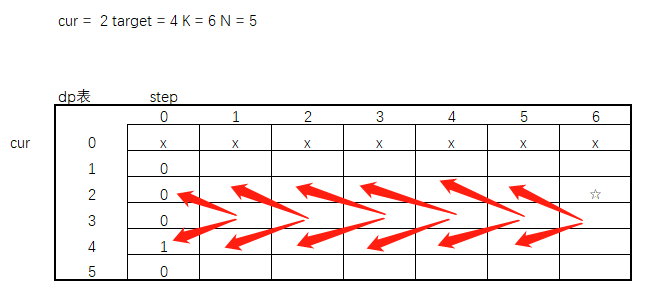
在根据代码，如果此时cur = 3，是不是将依赖结果进行相加，那此时dp表是不是就完整了。

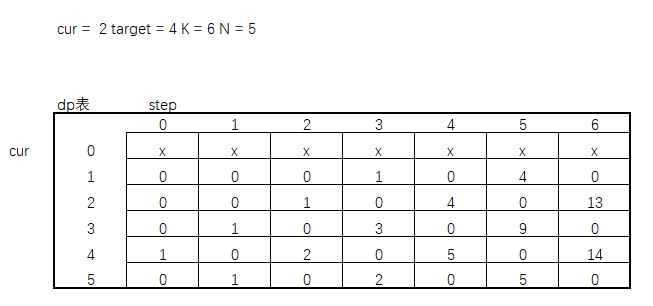
可以看到，cur = 2，step = 6时，一共13个方法解可到达target = 4的位置。此时如果将dp表直接构建出来，是不是就可以根据变量cur和step来直接获取到结果。

代码
整个动态规划代码很简洁。

public static int ways3(int cur, int K, int target, int N) {
    
    
        int[][] dp = new int[N + 1][K + 1];
		//先将对应target位置标1
		//初始化int[][]默认值都是0，所以其他值不用管
        dp[target][0] = 1;
		//按列遍历
        for (int step = 1; step <= K; step++) {
    
    
        	//先将第一列的值确定
            dp[1][step] = dp[2][step - 1];
            //因为我单独遍历N行时的值，所以这个遍历到 N -1即可
            for (int j = 2; j < N; j++) {
    
    
            	//按照依赖关系，当前位置依赖左上和左下的位置
                dp[j][step] = dp[j - 1][step - 1] + dp[j + 1][step - 1];
            }
            //再将最后一列的值确定
            dp[N][step] = dp[N - 1][step - 1];
        }

        return dp[cur][K];
    }