[AtCoder Regular Contest 096 E] Everything on It 解题报告 (第二类斯特林数+容斥原理)

题目链接：https://arc096.contest.atcoder.jp/tasks/arc096_c

Time limit : 4sec / Memory limit : 512MB

Score : 900 points

Problem Statement

In "Takahashi-ya", a ramen restaurant, basically they have one menu: "ramen", but N kinds of toppings are also offered. When a customer orders a bowl of ramen, for each kind of topping, he/she can choose whether to put it on top of his/her ramen or not. There is no limit on the number of toppings, and it is allowed to have all kinds of toppings or no topping at all. That is, considering the combination of the toppings, 2N types of ramen can be ordered.

Akaki entered Takahashi-ya. She is thinking of ordering some bowls of ramen that satisfy both of the following two conditions:

• Do not order multiple bowls of ramen with the exactly same set of toppings.
• Each of the N kinds of toppings is on two or more bowls of ramen ordered.

You are given N and a prime number M. Find the number of the sets of bowls of ramen that satisfy these conditions, disregarding order, modulo M. Since she is in extreme hunger, ordering any number of bowls of ramen is fine.

Constraints

• 2≤N≤3000
• 10^8≤M≤10^9+9
• N is an integer.
• M is a prime number.

Subscores

• 600 points will be awarded for passing the test set satisfying N≤50.

---

Input

Input is given from Standard Input in the following format:

N M

Output

Print the number of the sets of bowls of ramen that satisfy the conditions, disregarding order, modulo M.

---

Sample Input 1

Copy

2 1000000007

Sample Output 1

Copy

2

Let the two kinds of toppings be A and B. Four types of ramen can be ordered: "no toppings", "with A", "with B" and "with A, B". There are two sets of ramen that satisfy the conditions:

• The following three ramen: "with A", "with B", "with A, B".
• Four ramen, one for each type.

---

Sample Input 2

3 1000000009

Sample Output 2

118

Let the three kinds of toppings be A, B and C. In addition to the four types of ramen above, four more types of ramen can be ordered, where C is added to the above four. There are 118 sets of ramen that satisfy the conditions, and here are some of them:

• The following three ramen: "with A, B", "with A, C", "with B, C".
• The following five ramen: "no toppings", "with A", "with A, B", "with B, C", "with A, B, C".
• Eight ramen, one for each type.

Note that the set of the following three does not satisfy the condition: "'with A', 'with B', 'with A, B'", because C is not on any of them.

---

Sample Input 3

50 111111113

Sample Output 3

1456748

Remember to print the number of the sets modulo M. Note that these three sample inputs above are included in the test set for the partial score.

---

Sample Input 4

3000 123456791

Sample Output 4

16369789

题目大意：有 N 种调味剂, 现在要做一些拉面, 每碗拉面中可以放入任意种 类的调味剂, 但必须满足没有两碗拉面使用的调味剂集合相同, 且每种调味剂至少出现在两碗拉面中.

求方案数模一个质数.N ≤ 3000.

我们发现拉面是随便多少碗的，考虑容斥。定义调味剂不合法为调味剂只出现了1次或没有出现，ans=(0个调味剂不合法，其他任意) - (1个调味剂不合法，其他任意) + (2个调味剂不合法，其他任意)…………

写出来就是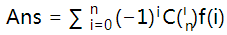,注意不合法的调味剂我们还要乘上组合数

f(i)是指有i个调味剂不合法，其他调味剂任意的方案数.

考虑怎么计算f[i]，f[i]=Σ(g[i][j]*2^(n−i)j)*2^{(2^(n-i))}

g[i][j]为在j碗面中有i种是不合法调味剂的方案数,然后剩下的n-i种调味剂可以随便放在这j碗面里，也可以放在j碗面之外(j<=i)

考虑放在j碗面里总共有 2^(n-i) 种放的状态，一共j碗面，方案数就是2^(n−i)j

考虑放在j碗面之外，同样有2^(n-i)种放的状态，每一种状态都有可能出现或者没有，方案数就是2^{(2^(n-i))}和上面那个之所以形式上不一样是因为这个不限制个数

预处理出组合数和g数组，g数组的递推式：g[i][j]=g[i-1][j-1]+g[i-1][j]*(j+1)（第二类斯特林数）。这样递推的原因是，当有i-1种坏酱在j-1碗面中时，第i种酱就必定在第j碗面中;或者i-1种酱在j碗面中，那第i种酱可以在任意j碗面中，或者压根就没加入任意j碗面中，所以是乘于j+1

值得注意的是，我们在计算2^{(2^(n-i))} 的时候，作为指数的(2^(n-i))取模并不是模上mod，而是模上mod-1，也就是mod的欧拉函数值（欧拉定理）

代码如下：

#include<iostream>
#include<cstdio>
#include<algorithm>
#define ll long long
using namespace std;

const int maxn=3e3+15; 
ll n,mod;
ll g[maxn][maxn],c[maxn][maxn];
ll mul(ll a,ll b,ll p)
{
    ll r=0;
    for (;b;b>>=1,a=(a+a)%p) if (b&1) r=(r+a)%p;
    return r;
}
ll qpow(ll a,ll b,ll p)
{
    ll r=1;
    for (;b;b>>=1,a=mul(a,a,p)) if (b&1) r=mul(r,a,p);
    return r;
}
int main()
{
    scanf("%lld%lld",&n,&mod);    
    for (int i=1;i<=n;i++)
    {
        c[i][0]=c[i][i]=1;
        for (int j=1;j<i;j++)
            c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
    }
    for (int i=0;i<=n;i++)
    {
        g[i][0]=1;
        for (int j=1;j<=i;j++)
            g[i][j]=(g[i-1][j-1]+g[i-1][j]*(j+1)%mod)%mod;    
    }
    ll ans=0;
    for (int i=0;i<=n;i++)
    {
        ll k=c[n][i];
        if (i&1) k=(mod-k)%mod;
        ll x=qpow(2,n-i,mod-1);//欧拉定理，注意模数
        x=qpow(2,x,mod);
        ll kind=qpow(2,n-i,mod);
        ll cnt=0,y=1;
        for (int j=0;j<=i;j++)
        {
            cnt=(cnt+(g[i][j]*y%mod))%mod;
            y=kind*y%mod;
        } 
        ans=(ans+(k*cnt%mod*x%mod))%mod;
    }
    printf("%lld\n",ans);
    return 0;
}