记忆化搜索与动态优化与背包问题

背包问题

动态规划（DP）—— 算法设计方法之一。

问题：有几个重量和价值分别为Wi和Vi的物品。从这些物品中挑选出总重量不超过W的物品，求所有挑选方案中价值总和最大的值。
限制条件
1<=n<=100
1<=Wi，Vi<=100
1<=W<=10000

输入样例：
n = 4
(w ,v) = { (2,3), (1,2),(3,4), (2,2) }
W=5;
输出样例：
7（选择0,1,3号）

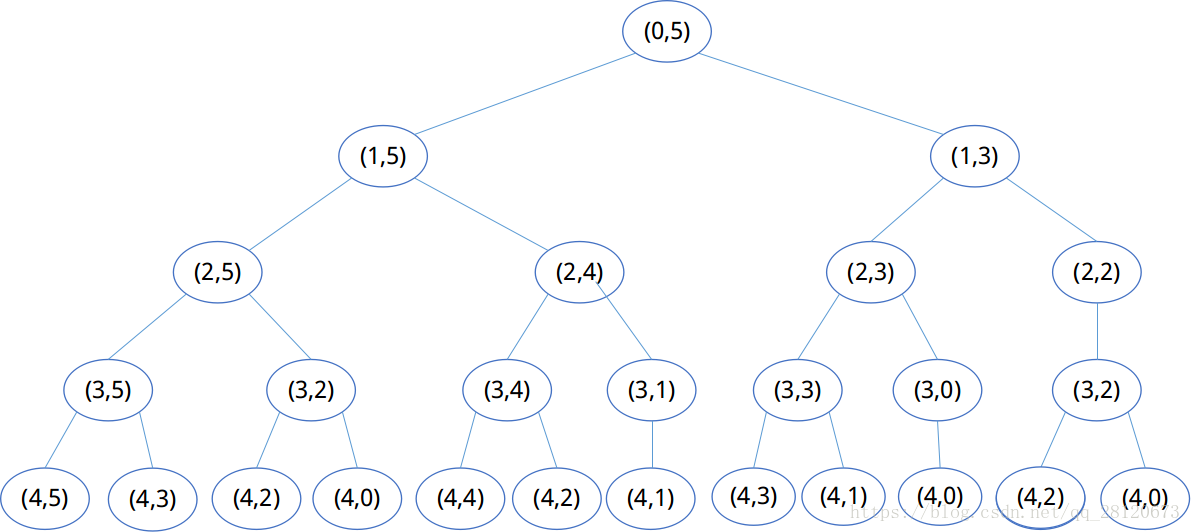
这种问题就是背包问题。背包问题看起来非常复杂，需要测试很多种组合。首先我们对每个物品是否放入背包进行搜索试试看。
代码如下：

#include <iostream>

#define MAX_N 100

using namespace std;

int n, W; //n个 物品， 总重量不超过W

int w[MAX_N], v[MAX_N];

//从第i个物品开始挑选总重量小于j的部分
int rec(int i, int j) {
    int res;
    if (i == n) {
        //已经没有剩下的了
        return res = 0;
    } else if (j < w[i]) {
        res = rec(i + 1, j);//这个物品超重了,尝试下一个
    } else {
        res = max(rec(i + 1, j), rec(i + 1, j - w[i]) + v[i]); //在这里进行分支前一个是不包含第i个，后一个是包含第i个。
    }
    return res;
}

void init() {
    cin >> n ;
    for (int i = 0; i < n; i++) {
        cin >> w[i];
        cin >> v[i];
    }
    cin>>W;
}

int main() {
    init();
    cout << rec(0, W) << endl;
    return 0;
}

虽然上述方法可以求解，但是显然这种方法不是很好。它的搜索深度为n，最坏情况需要$O(2^n)$时间复杂度。该递归调用方法使用了遍历二叉树搜索的原理。

其实这里是有改进的地方，观察二叉树会发现rec(3,2)执行了两次，但是如果我们在执行第一次的时候将rec(3,2)的值保存起来，那么下次执行时就可以直接调用结果了（这便是记忆化搜索）。
来试试新的方法：增加一个二维数组dp[][],将执行结果没一步保存在其中。

代码如下：

#include <iostream>

#define MAX_N 100

using namespace std;

int n, W; //n个 物品， 总重量不超过W

int w[MAX_N], v[MAX_N];
int dp[MAX_N][MAX_N];

//从第i个物品开始挑选总重量小于j的部分
int rec(int i, int j) {
    if (dp[i][j] != 0) {
        return dp[i][j]; //如果有记录则直接返回结果
    }
    int res;
    if (i == n) {
        //已经没有剩下的了
        return res = 0;
    } else if (j < w[i]) {
        res = rec(i + 1, j);//这个物品超重了,尝试下一个
    } else {
        res = max(rec(i + 1, j), rec(i + 1, j - w[i]) + v[i]); //在这里进行分支前一个是不包含第i个，后一个是包含第i个。
    }
    dp[i][j] = res;  //结果保存
    return res;
}

void init() {
    cin >> n;
    for (int i = 0; i < n; i++) {
        cin >> w[i];
        cin >> v[i];
    }
    cin >> W;
}

int main() {
    init();
    cout << rec(0, W) << endl;
    return 0;
}

仔细研究前面的算法用到的这个记忆数组。记dp[i][j]为根据rec的定义，从第i个物品开始挑选总重量小于j时，总价值最大的值。于是我们有一下递推公式。

$dp[n][j]=0$

$$dp[i][j]=\left\{ \begin{aligned} dp[i+1][j] (j<w[i]) \\ max( dp[i+1][j], dp[ii+1][j-w[i]+v[i]) \end{aligned} \right.$$
不用递归函数，直接使用地推公式将各项值计算出来，然后用二重信息即可解决该问题。

int dp[MAX_N+1][MAX_N+1] {}; //初始化为全0
void solve2(){
    for(int i=0;i<n-1;i--){
        for(int j=0;j<=W;j++){
            if(j<w[i]){
                dp[i][j]=dp[i+1][j];
            }else{
                dp[i][j]=max(dp[i+1][j] , dp[i+1][j-w[i]] + v[i]);
            }
        }
    }
}

虽然这个函数的时间复杂度与前一个相同$O(n×W)$ ,但是简明了许多。
动态规划问题（dp）可以分析其递推公式。

注意：全局数组和静态数组会被初始化为0；局部数据需要手动初始化为0，例如：int a[4]={} ; 或 int a[4] {} ; 或 int a[4] {0} 。如果括号里写0或什么都不写将会把数组全部初始化为0，但是如果这样写：int a[4] {1}; ，将会被初始化为1 0 0 0.

其他推导方法

递推公式有多种推导方法，使用不同的递推公式我们可以得到多种算法。

正向推导

刚讲到DP中关于i的循环是逆向进行的。如下递推公式是正向进行的。
$dp[i+1][j]:=$从前i个物品中挑选出总重量不超过j的物品时，总价值的最大值

$dp[0][j]=0$

$$dp[i+1][j]=\left\{ \begin{aligned} dp[i][j] ,(j<w[i]) \\ max( dp[i][j], dp[i][j-w[i]]+v[i]) \end{aligned} \right.$$

仔细观察公式会发现，dp中的i和w和v中的i不同，dp中的i表示前i个物品，而w和v中的i表示物品的编号，即编号是从0开始的。

void solve() {
    for (int i = 0; i < n; i++) {
        for (int j = 0; j <= W; j++) {
            if (j < w[i]) {
                dp[i + 1][j] = dp[i][j];
            } else {
                dp[i + 1][j] = max(dp[i][j], dp[i][j - w[i]] + v[i]);
            }
        }
    }
    cout<<dp[n][W];
}

除了使用地推公式外的其他方法

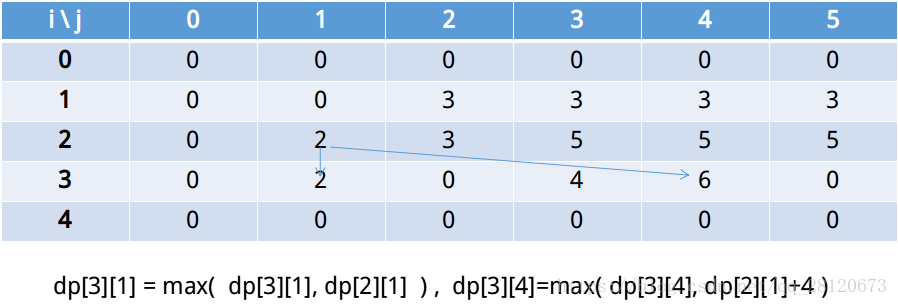
除了用递推方式逐项求解外，还可以把状态转换想象成从“前i个物品中挑选出总重量不超过j时的状态” 向“前i+1个物品中选取总重量不超过j“ 和 ”前i+1个物品中选取总重量不超过j+w[i] 时的状态“的转移，于是可以实现如下形式。

void solve2() {
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < W; j++) {
            dp[i + 1][j] = max(dp[i + 1][j], dp[i][j]);
            if (j + w[i] <= W) {
                dp[i + 1][j + w[i]] = max(dp[i + 1][j + w[i]], dp[i][j] + v[i]);//  dp[i+1][j+w[i]]表示前i+1个物品，重量不超过j+w[i]的价值，dp[i][j]+v[i],表前i个物品重量不超过j的价值，加上第i+1个物品的价值，也就是说，它和dp[i + 1][j + w[i]]相比默认选择了第i+1个物品。
            }
        }
    }
    cout << dp[n][W];

上述问题中，从当前状态转移到下一状态的形式，需要注意初项之外也需要初始化（在本问题中，因为价值的初始值为0，所以没有显示的初始化，在有些问题中初始值为无穷大等，需要显示的初始化。）
同一个问题可能有很多不同的解法：搜索记忆法、递推关系dp、状态转移dp等。根据具体的问题选择较好的方法。