0x01 什么是尺规作图?
一般定义
尺规作图是指用无刻度的直尺和圆规作图。
尺规作图是起源于古希腊的数学课题。
只使用圆规和直尺,并且只准许使用有限次,来解决不同的平面几何作图题。
尺规作图使用的直尺和圆规带有想像性质,跟现实中的并非完全相同:
1、直尺必须没有刻度,无限长,且只能使用直尺的固定一侧。只可以用它来将两个点连在一起,不可以在上画刻度;
2、圆规可以开至无限宽,但上面亦不能有刻度。它只可以拉开成之前构造过的长度。
严格定义
仅以“有限次使用无刻度的直尺和圆规作图”这样的措辞作为定义显然是不够严密的,因为不限定每“次”以内的操作复杂度的话,“有限次”就成无意义的了。
因此,一般采用的定义是基于“作图公法”的定义,即:
1. 每次的操作只能是公认允许的五项基本操作(称为五项作图公法)之一;
2. 每次操作之前,操作者为决定是否操作和进行哪种操作可以进行的逻辑判断,也只能是几何学中公认允许的几种。
基于“作图公法”的定义如下:
承认以下五项前提,有限次运用以下五项公法而完成的作图方法,就是合法的尺规作图:
五项前提:
1、允许在平面上、直线上、圆弧线上已确定的范围内任意选定一点(所谓“确定范围”,依下面四条的规则);
2、可以判断同一直线上不同点的位置次序;
3、可以判断同一圆弧线上不同点的位置次序;
4、可以判断平面上一点在直线的哪一侧;
5、可以判断平面上一点在圆的内部还是外部。
五项公法:
1、根据两个已经确定的点作出经过这两个点的直线;
2、以一个已经确定的点为圆心,以两个已经确定的点之间的距离为半径作圆;
3、确定两个已经做出的相交直线的交点;
4、确定已经做出的相交的圆和直线的交点;
5、确定已经做出的相交的两个圆的交点。
也有些资料上给出的五项公法的后两条中的“交点”改为“公共点”。这两种叙述差别在于后者多包括了“切点”。但是,因为确定切点即使不算基本操作,也是可以用其它基本操作组合实现的,所以,两种叙述的定义并无本质不同。
0x02 回顾初中课堂的知识
1、尺规可以做等角;
2、尺规可以做角平分线;
3、尺规可以做中点;
4、尺规可以做过一点的垂线,可以做过一点的平行线;
5、尺规可以做过三点的圆。
还有很多,但后文用到的都先放在这里。
0x03 尺规能做什么?
“尺规作图”,不只是做个图。人们对尺规作图的研究,实质上,可以说是对代数的研究。
任何作图问题,最后可以归结为作点;而作点,大多数可以归结为作实数。
和与差
每个线段长度是一个实数。这里我们假设“给定一个实数”意味着“给定一个线段,它的长度是给定的实数。
因此给定两个实数可以用尺规做出和与差。
乘积
给定两个实数能否用尺规做出乘积(能否做出以乘积为长度的线段)?答案是不能,还需要给定单位长,也就是1。这个原因也很简单,如果不给1,两个线段的长度的比值是确定的,但是各自的数值并不确定。
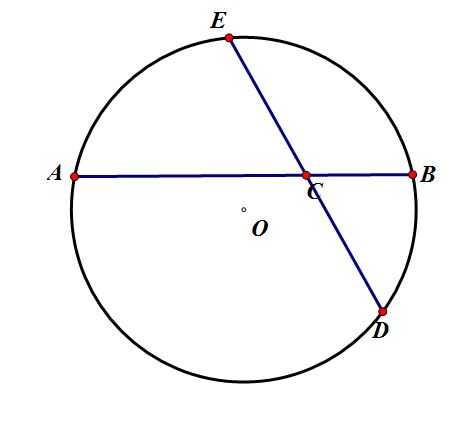
给定两个线段和1以后,就可以做出以其为乘积的线段了:
图中设AC、BC是给定的两个线段,1给定。过C任作一直线,直线上取E使得CE=1。做以ABE三点确定的圆(1.5),延长EC交此圆于D,CD即为以AC*BC为长度的线段。
除法
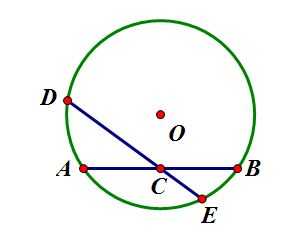
设给定线段长度为a和b,想要做出a/b,由于乘积的做法已经给出,所以只需要考虑1/b的做法。同理需要给定1。做法如下:
其中AC=BC=1,过C任作直线,取直线上一点D使得CD=b,做ABD三点确定的圆,延长DC交此圆于E,CE即为以1/b为长度的线段。
乘方与开方
有了乘积和除法,就有了整数幂的乘方(包括正整数幂和负整数幂,当然,和零次幂)。
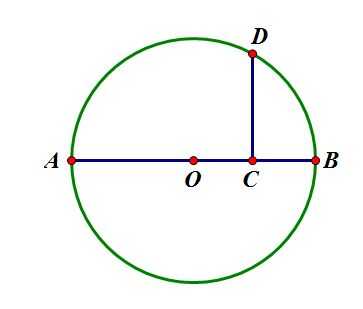
接下来是开方。设有实数a,当然给定1,如下可以做出长度为的线段:
如图,设AC=a,延长AC,直线AC上取B使得BC=1。取AB中点O,作以AB为直径的圆。过C做AB的垂线(1.4),交此圆于D。CD即为以为长度的线段。
结论
综上,从1和实数a、b出发,可以用尺规做出他们的和、差、积、商、以及开方。
用现代的代数观点来说,任何可以用有限次加减乘除和开方算出的实数,都可以用尺规作图做出。(当然,此处的作出,指的是作出以该实数为长度的线段。)
举个例子:
作线段中点,其实是已知1,作1/2;
作角分线,其实本质是作线段中点;
作三等分点、五等分点等等亦然;
作正五边形、正十七边形等,本质上是作一个角,而作角,用余弦定理略作处理,其实就是在作一个实数(就是说等腰三角形顶角为要做的角,两个等腰边为1,只要作出底边边长的实数就可以了)。
正因如此,很多尺规作图的问题,都可以解决了。
用有限次的加减乘除开方的数在实际应用中还是比较普遍的,所以大部分实际问题,尺规还是有施展的空间的。
比如:
作角分线、作正三角形、作正五边形、作正八边形、作正十七边形等等。
尺规,只能做这些么?
是的,只能做这些了。
经过后人们的证明,尺规的能力,仅限于做出有限次的加减乘除开方的实数,或者对已知实数进行有限次加减乘除开方的运算。
0x04 尺规作图不能做什么?
世界三大尺规作图难题(应该说是尺规不可作图题):
1、三等分角问题:给定一个任意角,如何用尺规将其三等分?
2、倍立方问题:给定一个正方体,如何做出其二倍体积的正方体?
3、圆化方问题:给定一个圆,如何做出与其面积相等的正方形?
可以看到,三个问题本质上都是“做一个实数”。圆化方,要用1作出π;倍立方,要作出;而三等分角,则是用1和a,作出 4-3x+a=0的根(这个需要一点计算,此处从略了)。问题演变成了如何用有限次加减乘除和开方作出这三个数。
那么到底可以么?当时的代数发展有限,大家还不能回答这个问题。
经过了很久的研究,大家才逐一的证明出这三个问题的不可作:
1、一般的三次方程的根不能用二次根式表示;
2、π是超越数,不是任何整系数有限次方程的根。
这样才彻底解决了三个难题。
有兴趣可以参考:
※以上内容整理自多个来源※