logistic regression算法原理及实现

逻辑回归所要学习的函数模型为y(x)，由x->y，x为样本，y为目标类别，即总体思想是任意给出一个样本输入，模型均能将其正确分类。实际运用中比如有邮箱邮件分类，对于任意一封邮件，经过模型后可将其判别为是否是垃圾邮件。

假如我们知道某类数据的条件概率分布函数P(y|x),则不管输入x是什么值，均能计算出输出y为特定值的概率，根据概率的大小，也就可以将其正确分类。因此我们需要做的就是找到一个尽可能近似P(y|x)的分布，使得对输入的分类准确度接近真实分布的准确度。

下面考虑二分类问题。

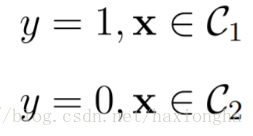
如果x属于数据C1类，则其经过模型后输出y为1的概率比y为0的概率要大，因此可将其归为y=1类，如果x属于数据C2类，则其经过模型后输出y为0的概率比y为1的概率要大则将其归为y=0类。即目标值只有0和1两，也即是二分类。

考虑下图

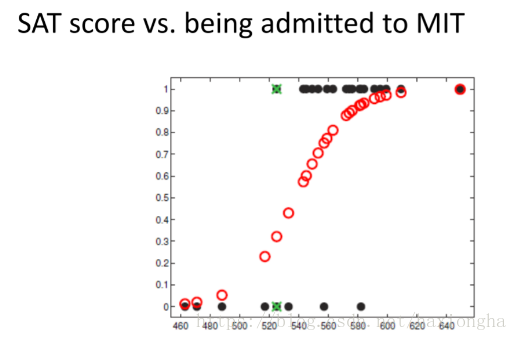
横坐标为学生分数，纵坐标为是否被录取，由图中黑点可知，分数低的大部分没有被录取，分数高的大部分被录取，其中个别数据为特殊情况，不予考虑。图中红色点就是我们的模型，其可根据不同的输入输出相应的值。

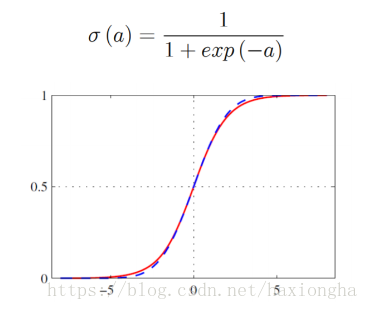
根据该曲线形状和输出范围，可以将sigmoid函数作为函数模型，函数表达式及图形如下：

因此

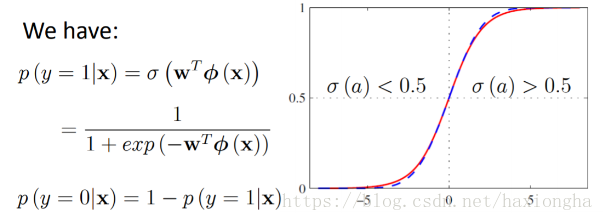
我们的目标值只有0和1，而该模型输出为0到1之间的值，为实现分类问题，可做如下处理：

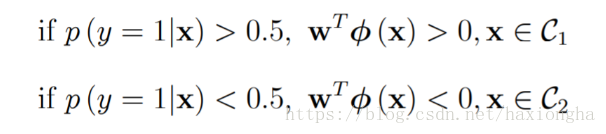
以上两条公式的物理解释为：因为概率的输出范围为[0,1]之间所有可能的值，而我们实际的分类问题只有两类0和1，那么现在就需要考虑实际样本输出的概率值为多大归为0类或者1类呢？最好的方式就是取中间值0.5作为分界点，输出目标值为1的概率大于0.5（说明其目标值接近1的概率更大）的归为1类，小于0.5（说明其目标值接近0的概率更大）的归为0类。

注意到函数模型中只有w为变量，那么我们接下来需要求出w使得我们的模型

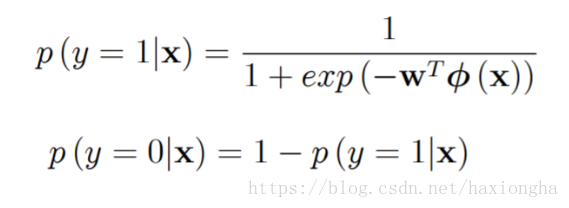
尽可能接近真实数据的分布，但是我们并不知道真实数据的分布，只知道由真实分布产生的样本数据，那么怎么根据样本数据使得求出的w使得模型尽可能接近真实分布呢？由此可以联想到最大似然估计，为什么最大似然估计就可以达到以上目的呢？似然函数表达式如下：

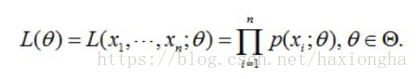
注意到，似然函数为每个样本的概率乘积，其中θ为似然函数变量，最大似然顾名思义就是求θ，使得似然函数L(θ)最大，换句话说，如果在特殊情况下，存在这么一个θ值，其同时使得每个样本的概率都为最大，那么自然似然函数也就是最大，则该θ就是我们所求的目标θ。但实际情况是很少存在这么一个θ值，使得所有样本概率为最大值同时成立，所以现在要退而求其次，找到这么一个θ值，使得总体概率为最大值，其中有部分样本概率可能为最大，也可能为最小或者介于两者之间，但他们总体的概率是最大的。

那么为什么最大似然估计可以估计真实分布模型呢？我的理解是这样的，从真实分布中采集一组样本，首先采集到的这组样本本身就隐含了某些性质，比如在真实分布中，这些样本发生的概率就比那些没有发生（即没有采集到）的样本概率一般更大，举个形象的例子，一个袋子里面有一个苹果和49个橘子，闭上眼睛从袋子中随便摸一个，毫无疑问，摸到橘子的概率会更大，如果将橘子当作一个样本，摸到就是样本发生，没摸到就是样本没发生，那么橘子这个样本发生的概率肯定大于苹果。换句话说，橘子这个样本发生的可能性更大，所以发生了的样本一般比没发生的样本概率更大。有了这个理解，接下来做更极端一点的假设，假设采集到的样本就是真实分布的所有样本容量（因为没采集到的概率很小，就忽略他们的存在），并且个数多于样本种类，那么必然会有样本被重复采集到，毫无疑问，被重复采集到的样本次数多的一般比那些采集次数少的更容易发生，即发生概率更大。

那么由这些采集到的样本就可以根据其频率次数与总的样本数比值确定相应样本的概率，这样就可以确定一个分布（又称之为经验分布），实际问题中我们就是将这个分布近似为真实数据发分布。 现在总结一下这里就是 P(采集次数多)>P(采集次数少)>P(没法生)。

现在回到我们逻辑回归问题，已知采集到的样本比没采集到的样本发生概率更大，甚至可以近似真实数据分布，那么对于我们含有参变量w的数学模型，只要求得w使得所有样本概率乘积最大，那么这时的w就会使得数学模型最接近真实数据分布。

考虑条件数据分布似然函数

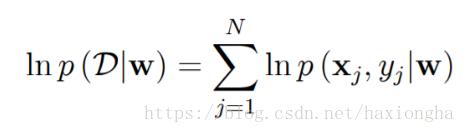
等式右边w为数据分布参数，大D为我们建立的数据分布模型，条件概率表示在已知w的情况下，数据分布模型也就相应的确定，现在就要找出这样一个w使得条件似然函数最大，也就是大D最接近我们真实的数据分布，等式右边为所有样本含参概率的积。根据概率链式法则，可将右边做如下变形：

$$p(x_j,y_j|w)=p(x_j|w)p(y_j|x_j,w)$$

两边同时取对数可得：

$$lnp(x_j,y_j|w)=lnp(y_j|x_j,w)+lnp(x_j|w)$$

所以数据分布似然函数可化为如下等式：

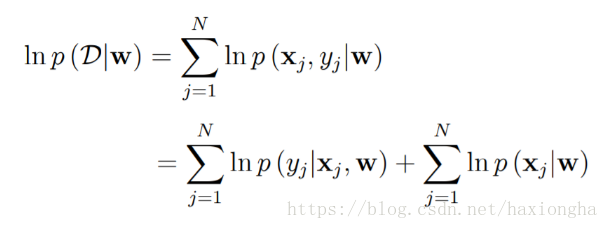
其中等式右边第二项x和w之间并没有联系，w的取值不会影响x，所以可将其看作一个常数，所以上式又可化为求如下最大似然值：

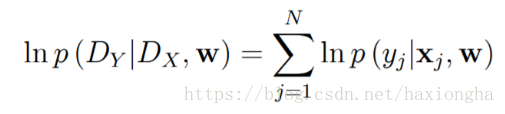
我们又已知：

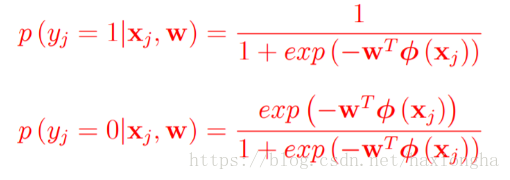
令

$$l(w)=\sum_{j=1}^Nlnp(y_j|x_j,w)$$

则有

$$\begin{aligned} l(w)&=\sum_{j=1}^Nlnp(y_j|x_j,w)\\&\\&=\sum_{x_j\in c1}lnp(y_j=1|x_j,w)+\sum_{x_j\in c_2}lnp(y_j|x_j,w)\\ &\\&=\sum_{j=1}^Ny_jlnp(y_j=1|x_j,w)+\sum_{j=1}^N(1-y_j)lnp(y_j=0|x_j,w)\\&\\&=\sum_{j=1}^Ny_jln(\frac{1}{1+\exp(-w^T\phi(x_j))}) +\sum_{j=1}^N(1-y_j)ln(\frac{\exp(-w^T\phi(x_j))}{1+\exp(-w^T\phi(x_j))})\\&\\&=\sum_{j=1}^N-y_jln(1+\exp(-w^T\phi(x_j))) +\\&\\& (1-y_j)[(-w^T\phi(x_j))-ln(1+\exp(-w^T\phi(x_j)))]\\&\\&=\sum_{j=1}^N[(y_j-1)(-w^T\phi(x_j))-ln(1+\exp(-w^T\phi(x_j)))] \end{aligned}$$

已知x和y均已知，现在需要求取w使得该似然函数为最大值。

令

$$\begin{aligned} E(w)&=-l(w)\\&\\&=\sum_{j=1}^N[(1-y_j)(w^T\phi(x_j))+ln(1+\exp(-w^T\phi(x_j)))] \end{aligned}$$

现在需要求取w使得函数E(w)最小，因此可以将其当作代价函数，代价函数为最小时的w值就是我们所需权重值。上式对w求导可得代价函数梯度函数如下：

$$\begin{aligned} \nabla{E(w)}&=\sum_{j=1}^N\{(1-y_j)\phi(x_j)-\frac{\exp(-w^T\phi(x_j))}{1+\exp(-w^T\phi(x_j))}\phi(x_j) \}\\&\\&=\sum_{j=1}^N\{\frac{1}{1+\exp(-w^T\phi(x_j))}\phi(x_j)-y_j\phi(x_j) \} \end{aligned}$$

让：

$$z_j=\frac{1}{1+\exp(-w^T\phi(x_j))}=\sigma(w^T\phi(x_j))$$

所以梯度函数可以写成：

$$\begin{aligned} \nabla{E(w)}&=\sum_{j=1}^N\{(z_j-y_j)\phi(x_j) \}\\\\&=\sum_{j=1}^N\{(\sigma(w^T\phi(x_j))-y_j)\phi(x_j) \} \end{aligned}$$

写成向量形式有：

$$\begin{aligned} \nabla{E(w)}&=\left[\phi(x_1),\phi(x_2)...,\phi(x_N)\right] \left[ \begin{matrix} (z_1-y_1)\\ (z_2-y_2)\\ .\\ (z_N-y_N)\end{matrix} \right]\\&\\&=\Phi^T(\vec{z}-\vec{y}) \end{aligned}$$

传统的方法一般可以用求梯度值为0时的w，即可使得E(w)函数为最小值，但实际情况下E(w)函数是一个关于w的凸函数，梯度函数没有闭式0解，因此采用牛顿迭代法求取最优w使得该函数梯度值为0。
由牛顿迭代法公式可知需要求出E(w)的二阶梯度

已知：

$$\frac{d\sigma(x)}{dx}=\sigma(a)[1-\sigma(a)]$$

所以有：

$$\begin{aligned} \nabla^2{E(w)}&=\frac{d^2E}{dwdw^T}\\\\&=\sum_{j=1}^N\sigma(w^T\phi(x_j))[1-\sigma(w^T\phi(x_j))]\phi(x_j)\phi(x_j)^T\\\\&=\sum_{j=1}^Nz_j(1-z_j)\phi(x_j)\phi(x_j)^T\\\\&=[\phi(x_1,\phi(x_2),...,\phi(x_N)] \left[\begin{matrix} z_1(1-z_1)&&&\\&z_2(1-z_2)\\&&..\\&&&z_N(1-z_N) \end{matrix}\right]\left[\begin{matrix} \phi^T(x_1)\\\phi^T(x_2)\\.\\\phi^T(x_N) \end{matrix}\right]\\&=\Phi^TR\Phi \end{aligned}$$

其中R是NXN的对角矩阵，它的每一个元素为:

$$R_{jj}=z_j(1-z_j)$$

最终权重更新公式为：

$$w^{new}=w^{old}-(\Phi^TR\Phi)^{-1}\Phi^T(\vec{z}-\vec{y})$$

逻辑回归代码例程

import scipy.io as scio
import matplotlib.pyplot as plt
import tensorflow as tf
import  numpy as np

file_x = scio.loadmat('ex4x.mat');                 #导入的数据为dict数据类型，前一部分为数据信息说明，后一部分数据是以array方式存放
file_y = scio.loadmat('ex4y.mat');
data_x = file_x['x']                               #因为数据存放的关键字为'x',提取dict中的array元素另存为data_x
data_y = file_y['y']
data_x = np.mat(data_x)                            #因为后面有矩阵的运算，所有将array转为矩阵数据类型
in_1 = np.ones((80,1),dtype=np.float64)
# in_1 = np.mat(in_1)                              #生成全1列矩阵
data_x=np.column_stack((in_1,data_x))              #给矩阵增加全1列  np.row_stack：给矩阵增加行
data_y = np.mat(data_y)                            #生成矩阵
#获取矩阵的维度，行数和列数
data_x_dim = data_x.shape                         #获取数据的维数

m = data_x_dim[0]                                 #m表示行数
n = data_x_dim[1]                                 #n表示列数

plot_x = data_x[:,1]                            #获取data_x第二列数据
plot_y = data_x[:,2]                            #获取data_x第三列数据
plot_x = np.array(np.transpose(plot_x))         #画图时，参变量只能是一维的
plot_y = np.array(np.transpose(plot_y))
plot_x1 = plot_x[:,1:40]                        #第一类数据
plot_y1 = plot_y[:,1:40]

plot_x2 = plot_x[:,41:80]                       #第二类数据
plot_y2 = plot_y[:,41:80]



#以上为数据处理和画图部分，下面进行逻辑回归及牛顿迭代
w =np.mat(np.zeros((n,1),dtype=np.float64))       #初始化所有权重为0
z = data_x*w                                      #
m_1_ones = np.mat(np.ones((m,1)))
h = m_1_ones /(1+np.exp(-z))                      #定义逻辑回归模型，此为向量形式

max_iteration=20                                  #设置迭代最大次数
thred = 0.0001                                    #牛顿迭代精度
count=1                                           #实际迭代次数
cost_now=0                                        #更新后的代价函数
while 1:
    count = count + 1
    z = data_x*w
    m_1_ones = np.mat(np.ones((m,1)))
    h = m_1_ones /(1+np.exp(-z))
    cont_pre=cost_now
    error = np.multiply(data_y , np.log(h)) + np.multiply((1-data_y) ,(np.log(np.mat(np.ones((m,1))-h))))         #代价函数定义
    cost_now=error.sum(axis=0)                                   #当前代价函数值
    if(abs(cost_now-cont_pre)<=thred) or (count>max_iteration):                           #迭代终止条件
        break
    iteration_error = h-data_y                                       #迭代误差
    G = (np.transpose(data_x)*iteration_error)/m                     #代价函数一阶导
    a1= np.matrix.tolist(np.transpose(h))                            #以下7行是为了生成对角矩阵所做的操作
    b1 = tuple(a1[0])
    c1 = np.diag(b1)
    a2= np.matrix.tolist(np.transpose((1-h)))
    b2 = tuple(a2[0])
    c2= np.diag(b2)
    r = c1*c2
    H = (np.transpose(data_x)*r*data_x)/m                           #计算代价函数二阶导
    w = w -H.I*G                                                    #牛顿迭代法求解

fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.scatter(plot_x1,plot_y1,marker='+',color='r')
ax.scatter(plot_x2,plot_y2,marker='o',color='g')
x_ax = plot_x
y_ax = (-w[0]-w[1]*plot_x)/w[2]
ax.plot(x_ax,y_ax,marker='o',color='b')
plt.ion()
plt.show()
input()

文件参考链接：
ex4x.mat
ex4y.mat
手写数字分类问题

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import warnings
warnings.filterwarnings("ignore")
mnist = input_data.read_data_sets('MNIST_data', one_hot=True)

xs = tf.placeholder(tf.float32, [None, 784])  # 28x28
ys = tf.placeholder(tf.float32, [None, 10])


def add_layer(inputs, in_size, out_size, activation_function=None):
    Weight = tf.Variable(tf.random_normal([in_size, out_size]))  # 初始化in_size x out_size大小的参数矩阵
    biases = tf.Variable(tf.random_normal([1, out_size]) + 0.1)  # 初始化偏移量
    Wx_plus_b = tf.matmul(inputs, Weight) + biases
    if activation_function is None:
        outputs = Wx_plus_b
    else:
        outputs = activation_function(Wx_plus_b)
    return outputs


def compute_accuracy(v_xs, v_ys):
    global precdition
    y_pre = sess.run(precdition, feed_dict={xs: v_xs})
    correct_precdition = tf.equal(tf.argmax(y_pre, 1), tf.argmax(v_ys, 1))
    accuracy = tf.reduce_mean(tf.cast(correct_precdition, tf.float32))
    result = sess.run(accuracy, feed_dict={xs: v_xs, ys: v_ys})
    return result


precdition = add_layer(xs, 784, 10, activation_function=tf.nn.softmax)
cross_entropy = tf.reduce_mean(-tf.reduce_sum(ys * tf.log(precdition), reduction_indices=[1]))
train_step = tf.train.GradientDescentOptimizer(1).minimize(cross_entropy)  # learning_rate=0.5
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for i in range(1000):
        batch_xs, batch_ys = mnist.train.next_batch(100)
        sess.run(train_step, feed_dict={xs: batch_xs, ys: batch_ys})
        if i % 50 == 0:
            print(compute_accuracy(mnist.test.images, mnist.test.labels))