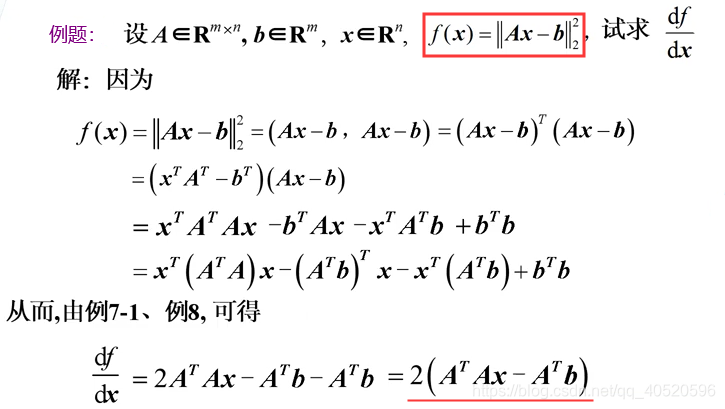计算方法(向量/矩阵微分)
其他
2020-03-27 14:42:39
阅读次数: 0

-
f(x)=(x,a)=aTx=xTa 因此dxdf=a
-
f(x)=xTAx 因此dxdf=(A+AT)x
-
f(x)=∥Ax−b∥22 因此dxdf=2AT(Ax−b)
1. 向量乘积的微分

2. 向量与矩阵乘积的微分

3. 矩阵范数的微分
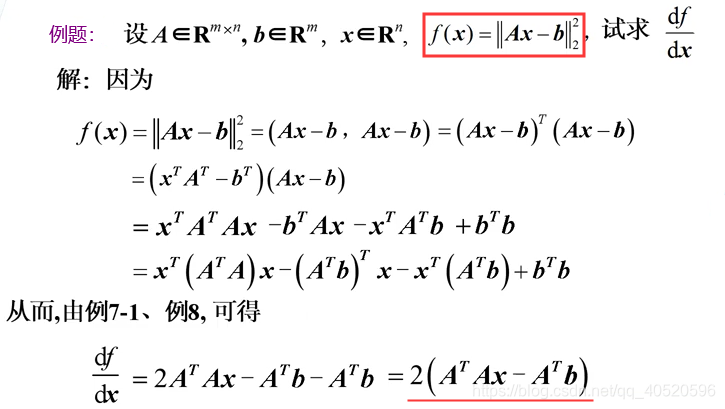
发布了61 篇原创文章 ·
获赞 44 ·
访问量 11万+
转载自blog.csdn.net/qq_40520596/article/details/105138453