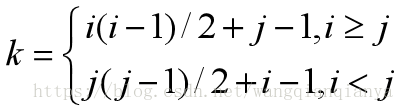树
二叉树
性质1:二叉树的第i层至多有 2^(i-1) 个结点(i≥1)
性质2:深度为h的二叉树至多有 2^h –1 个结点(h≥1)
性质3:n0 = n2 + 1 { 结点总数 : n = n0 + n1 + n2 分支数 :n-1 = n1 + 2n2 }
{ e.g : 若包含有n个结点的树中只有叶子结点和度为k的结点,则该树中有多少叶子结点?
解 :n = n0+nk, n-1 = knk => n0 = n-(n-1)/ k }
满二叉树:指的是深度为k且含有2^k-1个结点的二叉树
完全二叉树:树中所含的n个结点和满二叉树中编号为1至n的结点一一对应
对于深度为k的完全二叉树,则1) 前k-1层为满二叉树;2) 第k层结点依次占据最左边的位置;3) 一个结点有右孩子,则它必有左孩子;4) 度为1的结点个数为0或1 5) 叶子结点只可能在层次最大的两层上出现;6) 对任一结点,若其右分支下的子孙的最大层次为l, 则其左分支下的子孙的最大层次必为l或l+1。
性质4:具有n个结点的完全二叉树的深度为 ┗log2n』+1
{ 由性质2 2^(k-1) -1 < n ≤ 2^k -1 或 2^k -1 ≤ n < 2^k 于是 k-1 ≤ log2n < k }
性质5:如果对一棵有n个结点的完全二叉树的结点按层序编号(从第1层到第 ╙log2n』+1 层,每层从左到右),则对任一结点i (1 ≤ i ≤ n),有(1) 如果i=1,则结点i是二叉树的根,无双亲;如果i >1, 则其双亲是结点 └i/2』 ;(2) 如果2i > n,则结点i无左孩子(结点i为叶子结点);否则其左孩子是结点2i ;(3) 如果2i + 1> n,则结点i无右孩子;否则其右孩子是结点2i + 1。
a、一般二叉树的顺序存储方法通过补虚结点,将一般的二叉树变成完全二叉树,但空间开销大!
线索二叉树——二叉树的结构扩展
二叉树的遍历:非线性结构的线性化
问题:在二叉树的链式存储中,如何快速找到某结点在某一序列(先序/后序/中序)中的直接前驱和直接后继?
为每一结点增加fwd和bkwd指针域——降低了存储密度
利用二叉链中的空链域(n个结点有n+1个空链域) ——需要标识链域的含义(指向孩子?线索?)
实现】
在有n个结点的二叉链表中必定有n+1个空链域
在线索二叉树的结点中增加两个标志域
ltag :若 ltag =0, lchild 域指向左孩子;
若 ltag=1, lchild域指向其前驱
rtag :若 rtag =0, rchild 域指向右孩子;
若 rtag=1, rchild域指向其后继
如何建立线索链表?
在中序遍历过程中修改结点的左、右指针域,以保存当前访问结点的“前驱”和“后继”信息。遍历过程中,附设指针pre,并始终保持指针pre指向当前访问的、指针p所指结点的前驱。
先根(次序)遍历:若树不空,则先访问根结点,然后依次先根遍历各棵子树。
后根(次序)遍历:若树不空,则先依次后根遍历各棵子树,然后访问根结点。
按层次遍历:若树不空,则自上而下自左至右访问树中每个结点。
森林的遍历
先序遍历(对森林中的每一棵树进行先根遍历)
若森林不空,则 访问森林中第一棵树的根结点; 先序遍历森林中第一棵树的子树森林; 先序遍历森林中(除第一棵树之外)其余树构成的森林。中序遍历(对森林中的每一棵树进行后根遍历)
若森林不空,则 中序遍历森林中第一棵树的子树森林; 访问森林中第一棵树的根结点; 中序遍历森林中(除第一棵树之外)其余树构成的森林
先根遍历 对应二叉树的先序遍历 后根遍历 对应二叉树的中序遍历
最优树
路径长度:路径上的分支数目
树的路径长度:树根到每一结点的路径长度之和结点的带权路径长度:该结点到树根之间的路径长度与结点上权的乘积
树的带权路径长度:树中所有叶子结点的带权路径长度之和
查找
关键字(key)是数据元素中某个数据项的值,用它可以标识(识别)一个数据元素。若此关键字可以唯一地标识一个元素,则称此关键字为主关键字(Primary key)(对不同的元素,其主关键字均不同)。反之,称用以识别若干元素的关键字为次关键字(secondary key)。当数据元素只有一个数据项时,其关键字即为该数据元素的值。索引顺序表 = 索引 + 顺序表
二叉排序树
或者是一棵空树;或者是具有如下特性的二叉树:(1)若它的左子树不空,则左子树上所有结点的值均小于根结点的值;(2)若它的右子树不空,则右子树上所有结点的值均大于根结点的值;(3)它的左、右子树也都分别是二叉排序树
中序遍历二叉排序树可得到一个关键字的有序序列
和插入相反,删除在查找成功之后进行,并且要求在删除二叉排序树上某个结点之后,仍然保持二叉排序树的特性。可分三种情况讨论:
1)被删除的结点是叶子;
仅需修改其双亲结点的相应指针即可
(2)被删除的结点只有左子树或者只有右子树;
将其左子树或右子树直接链接到其双亲结点成为其双亲的子树
(3)被删除的结点既有左子树,也有右子树。
将“前驱”替代被删数据元素,即将被删结点的数据元素赋值为它的 "前驱",然后从二叉查找树上删去这个"前驱"结点,使得删除一个结点之后的二叉查找树上其余结点之间的"有序"关系不变,而其前驱结点由于只有左子树容易删除。
平衡二叉树
特点为:左、右子树深度之差的绝对值不大于1。
平衡因子定义为左子树的深度-右子树的深度
构建方法
每插入一个新结点时,AVL树中相关结点的平衡状态会发生改变。因此,在插入一个新结点后,需要从插入位置沿通向根的路径回溯,检查各结点的平衡因子(左、右子树的高度差)。如果在某一结点发现高度不平衡,停止回溯。
从发生不平衡的结点起,沿刚才回溯的路径取直接下两层的结点。如果这三个结点处于一条直线上,则采用单旋转进行平衡化。单旋转可按其方向分为左单旋转和右单旋转,,其方向与不平衡的形状相关。
如果这三个结点处于一条折线上,则采用双旋转进行平衡化。双旋转分为先左后右和先右后左两类。
先左后右: C代A,C儿两边分,左儿到B右,右儿到A左
先右后左: C代A,C儿两边分,左儿到A右,右儿到B左
哈希表
基本思想:在记录的存储地址和它的关键字之间建立一个确定的对应关系;这样,不经过比较,一次存取就能得到所查元素
定义
哈希函数——在记录的关键字与记录的存储地址之间建立的一种对应关系叫~
哈希函数的构造方法
除留余数法
构造:取关键字被某个不大于哈希表表长m的数p除后所得余数作哈希地址,即H(key)=key MOD p,p<=m
处理冲突的方法
1、开放定址法
方法: 为产生冲突的地址H(key)求得一个地址序列: H0, H1, H2, …, Hk 1≤k≤m-1 其中:H0 = H(key) ——哈希函数
Hi = ( H(key) + di ) MOD m i=1, 2, …,k
m——哈希表表长 di——增量序列
(增量 di 有三种取法)
线性探测再散列: di =1,2,3,……m-1
二次探测再散列: di =1²,-1²,2²,-2²,3²,……±k²(km/2)
伪随机探测再散列: di =伪随机数序列
2、再哈希法
方法:构造若干个哈希函数,当发生冲突时,计算下一个哈希地址,即:Hi=Rhi (key) i=1,2,……k
其中:Rhi——不同的哈希函数
特点:不易产生“聚集”,但计算时间增加
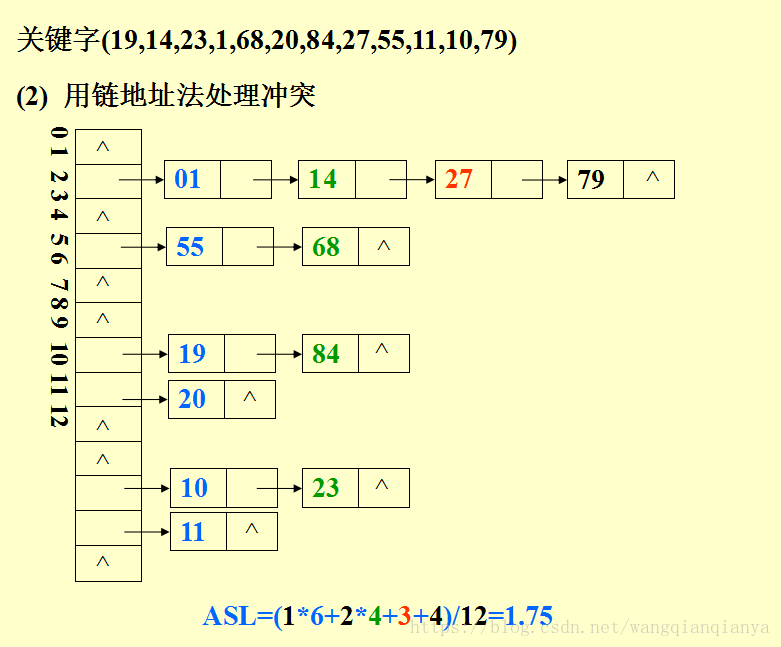
链地址法
方法:将所有关键字为同义词的记录存储在一个单链表中,并用一维数组存放头指针建立一个公共溢出区
数组和广义表
LOC[i,j] = LOC[0,0] + (b2×i+j)L
特殊矩阵
三角矩阵
对角矩阵
Loc(aij)=Loc(a11)+2(i-1)+(j-1)
稀疏矩阵
特点:非零元较零元少,且分布没有一定规律的矩阵
压缩存储原则:只存矩阵的行列数和每个非零元的行列下标及其值

(5,2,18), (6,1,15), (6,4,-7) } 和行列值(6,7)唯一确定
#define MAXSIZE 12500 // 假设非零元个数的最大值为12500
typedef struct {
int i, j; // 该非零元的行下标和列下标
ElemType e;
} Triple; // 三元组类型
typedef struct {
Triple data[MAXSIZE + 1]; // 非零元三元组表,data[0]未用
int mu, nu, tu; // 矩阵的行数、列数和非零元个数
} TSMatrix; // 稀疏矩阵类型
求转置矩阵
方法一:对原矩阵从第一行p(从1开始到非零元个数)开始遍历列,遇到列等于col(从1到原矩阵的列数,即转置矩阵的行数),赋值
Status TransposeSMatrix(TSMatrix M, TSMatrix &T)
{
T.mu=M.nu; T.nu=M.mu; T.tu=M.tu;
if (T.tu) {
q=1;
for (col=1;col<=M.nu;++col)
for(p=1;p<=M.tu;++p)
if (M.data[p].j==col){
T.data[q].i=M.data[p].j; T.data[q].j=M.data[p].i;
T.data[q].e=M.data[p].e; q++; }
}
return ok;
}
方法二:快速转置
实现:设两个数组
num[col]:表示矩阵M中第col列中非零元个数
cpot[col]:指示M中第col列第一个非零元在mb中位置
显然有:cpot[1]=1;
cpot[col]=cpot[col-1]+num[col-1]; (2<=col <=M.nu)
Status FastTransposeSMatrix(TSMatrix M, TSMatrix &T) {
T.mu = M.nu; T.nu = M.mu; T.tu = M.tu;
if (T.tu) {
for (col=1; col<=M.nu; ++col) num[col] = 0;
for (t=1; t<=M.tu; ++t) ++num[M.data[t].j];
cpot[1] = 1;
for (col=2; col<=M.nu; ++col)
cpot[col] = cpot[col-1] + num[col-1];
// 求 M 中每一列的第一个非零元在 b.data 中的序号
for (p=1; p<=M.tu; ++p) { // 转置矩阵元素
col = M.data[p].j; q = cpot[col];
T.data[q].i =M.data[p].j; T.data[q].j =M.data[p].i;
T.data[q].e =M.data[p].e; ++cpot[col];
} // for
} // if
return OK;
} // FastTransposeSMatrix