树形结构是复杂数据结构中最为简单的一类结构;树形结构不但本身很有用,还反映了许多计算过程的抽象结构;树形结构的结点形成一种层次结构;
树和链表、队列、栈等结构一样,也是一些基本元素的汇集,单元素之间不是简单的线性关系(在一个包含 n 个元素的数据结构里),可能存在更为复杂的联系。这种情况下,在一个包含 n个元素的数据结构里,元素之间的最远距离就不是 n,可能小得多。
树形结构也是由结点(结构中的逻辑单元,可用于保存数据)和结点之间的连接关系(一种后继关系)构成,但其结构与线性结构(表)不同,最重要的特征包括:
一个结构如果不空,其中就存在着唯一的一个起始节点,成为树根(root)
按结构的连接关系,树根外的其余结点都有且只有一个前驱(这点与线性结构一样),但另一方面,一个结点可以有 0 个或者多个后继(与线性结构不同)。另外,在非空的树结构中一定有些结点并不连接到其他结点。这种结点与表的尾节点性质类似,但在一个树结构里可以存在多个这种节点。
结构里的所有结点都在树根结点通过后继关系可达的结点集合里。换句话说说,从树根节点出发,经过若干次后继关系可以到达结构中的任一个结点;
结点之间的联系不会形成循环关系,这也就说明,结点之间的联系形成了一种序,但一般而言不像线性表那样形成一个全序;
从这种结构里的任意两个不同结点出发,通过后继关系可达的两个结点集合,或者互不相交,或者一个集合是另一个集合的子集;
特点:1、树中的每个节点至多关联到两个后继结点,即一个结点的关联节点数可以为0、1或2.
2、一个节点关联的后继结点明确的区分左右,或为其左关联结点,或为其右关联结点。
定义: 二叉树是结点的有穷集合。这个集合或者是空集,或者其中有一个称为根节点的特殊节点,其余节点分属两颗不相交的二叉树,这两颗二叉树分别是原二叉树(或说是原二叉树的根节点)的左右子树。
二叉树性质及结论的证明,天然地依赖于递归,而涉及到递归时,一般采用的证明方法为:数学归纳法
几个基本概念:
1、一个结点的子结点个数称为该结点的
度数。二叉树中树叶结点的度数为0,分支结点的度数可以是1或者2.
2、从一个祖先结点到其任何子孙结点都存在一系列边,形成从前者到后者的联系。这样一系列首尾相连的边称为树中的一条
路径,路径中边的条数称为该路径的
长度
3、
规定树根的层数为0,从树根到树中任一结点的路径长度就是该结点所在的层数,也就是该
结点的层数
4、
树的高度(深度)是树中结点的最大层数,也是树里最长路径的长度。
二叉树的性质:
1、
二叉树最重要的性质是树的高度和树中可以容纳的最大结点的个数之间的关系。(长为n的表里只能容纳n个结点,而在高为h的二叉树中则可以容纳大约n**h个结点)
2、
在非空二叉树第i层中最多有2**i个结点(i>=0)
数学归纳法进行证明,
i→2ii→2i
⇒
i+1→2i⋅2=2i+1i+1→2i⋅2=2i+1
3、
高度为h的二叉树之多有2**(h+1)-1个结点(h>=0)
20+21+⋯+2h=2h+1−12−120+21+⋯+2h=2h+1−12−1
4、
对于任何非空二叉树T,如果其叶节点的个数为n0,度数为2的节点个数为n2,那么n0=n2+1
可以根据二叉树的 5 种不同形态,通过数学归纳法进行证明,由于条件中说了非空,那么只需考虑后续的 4 种形态。设 TT 是二叉树,L(T)L(T) 表示 TT 中叶节点的个数,B(T)B(T) 表示 TT 中度数为 2 的结点的个数。
显然对于单点二叉树,结论是成立的;
归纳 1:如果二叉树 TT包含根节点 rr 且只有左子树 T1T1,根据归纳假设,L(T1)=B(T1)+1L(T1)=B(T1)+1,又整个二叉树
归纳 2:如果原二叉树 TT 包含根节点 rr 和非空左右子树 T1,T2T1,T2,由归纳假设:
L(T1)=B(T1)+1L(T2)=B(T2)+1
又对整颗二叉树而言,L(T)=L(T1)+L(T
L(T)=L(T1)+L(T2),B(T)=B(T1)+B(T2)+B(T)=B(T1)+B(T2)+1(加1是因为根节点r的度数为2)
所以:
L(T)=B(T)+1
L(T)=B(T)+1
如果二叉树中所有分支节点的度数都是2,则称它为一个
满二叉树。
5、满二叉树数的节点个数为2**i, 叶节点比分支节点多一个(n0=n2+1)
对二叉树T,加入足够多的新叶结点,使T的原有结点都变成度数为2的分支结点,得到的二叉树称为T的
扩充二叉树。(
空树的扩充二叉树规定为空树; 任何二叉树的扩充二叉树都是满二叉树;扩充二叉树的外部结点的个数比内部结点的个数多1)
6、(扩充二叉树的内部和外部路径长度)扩充二叉树的外部路径长度E是从树根到树中各外部结点的路径长度之和,内部路径长度I是从树根到树中各内部结点的路径长度之和。如果该树有n个内部结点,那么E=I+2xN。
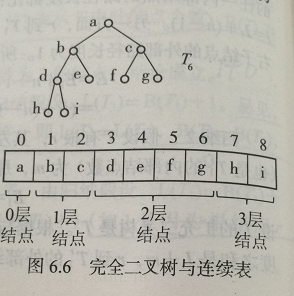
对于一颗高度为h的二叉树,如果其第0层至第h-1层的结点都满(也就是说,对所有0<<i<<h-1,第i层有2**i个结点)。如果最下一层结点不满,则所有结点在最左边连续排列,空位都在右边。这样的二叉树就是一棵完全二叉树。
7、n个结点的完全二叉树高度h=[log2n], 即为不大于log2n的最大整数。
8、如果n个结点的完全二叉树的结点按层次并按从左到右的顺序从0开始编号,对任一结点i(0<<i<<n-1)都有:
a. 序号为0的结点是根
b. 对于i>0, 其父结点的编号是(i-1)/2
c. 若2 x i + 1 < n, 其左子结点序号为2 x i +1, 否则它无左子结点
d. 若2 x i + 2 < n, 其右子结点序号为2 x i +2, 否则它无右子结点
完全二叉树使其可以方便地存入一个表或数组,直接根据元素下标就能找到一个结点的子结点或父结点。