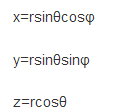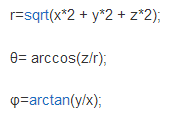因为题主是从光学角度提问的,下面就从光学角度出发作答,当然实际上无法绕开数学。
球谐函数和振动有关,从某种意义上来说,它和三角函数没什么区别。因为它们只是在“不同坐标系”下描述“不同方向”的振动。
我们知道,麦克斯韦方程导出的波动方程:

(均匀各向同性介质)是描述许多光学现象的出发点。直接假定场在时间上是简谐振动的  (单色光分析),立刻就有
(单色光分析),立刻就有 ,其中:
,其中:

当然这个方程可以描述很多种现象,如果把E理解为温度T,并取:

这就是稳态热扩散方程;如果把 理解为特征值,这就是单自由粒子的定态薛定谔方程。所以这个方程的解,及其表现出的一系列振动特征,在许多领域都是普适的。
理解为特征值,这就是单自由粒子的定态薛定谔方程。所以这个方程的解,及其表现出的一系列振动特征,在许多领域都是普适的。
我们通常会在3种坐标系下求解这个方程,也就是矩坐标、柱坐标、球坐标。
球坐标系:
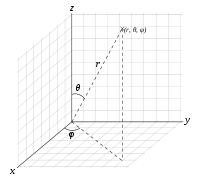
球坐标和直角坐的互换:
具体应用,在光学中,比如矩形腔、矩形波导,圆柱腔、圆柱波导,球型腔。热学中,可以有方块、圆柱、球的热扩散问题。量子力学里可以有方势阱、柱状阱、有心力场(氢原子)中的粒子运动问题。
每种坐标系都有3个方向,矩坐标系x、y、z,柱坐标系 ,球坐标系
,球坐标系 。上述方程在每种坐标系的每个方向上都会形成特定的振荡形态(有时会出现衰减或放大形态)。球谐函数
。上述方程在每种坐标系的每个方向上都会形成特定的振荡形态(有时会出现衰减或放大形态)。球谐函数 描述的就是球坐标系中在
描述的就是球坐标系中在 方向的振荡形态。这件事通过分离变量法可以看得很清楚。
方向的振荡形态。这件事通过分离变量法可以看得很清楚。
方程的具体求解都是通过分离变量进行的,具体是:
矩坐标: 
柱坐标 :
球坐标 :
具体求解过程教科书上都有,这里不再赘述,只看结果。注意,分离变量后的每一个子函数都描述了一个特定方向的形态。
矩坐标系的处理在数学上是最容易的,我们知道三个方向都有相似的振荡模式,由三角函数描述,比如 、
、 ,一般写为
,一般写为 。如果
。如果 是实数,就是一个振荡;如果是虚数,就是一个指数衰减(或放大)。
是实数,就是一个振荡;如果是虚数,就是一个指数衰减(或放大)。
在柱坐标系中, 和矩坐标系没什么区别,也是
和矩坐标系没什么区别,也是 的形式。
的形式。 的解是贝塞尔函数,注意,贝塞尔函数
的解是贝塞尔函数,注意,贝塞尔函数 和
和 描述的就是径向振荡形态,
描述的就是径向振荡形态, 和
和 描述的是径向放大或衰减形态。这和
描述的是径向放大或衰减形态。这和 有相似的意义。
有相似的意义。 具有
具有 形式的解,也是一个振荡(由于
形式的解,也是一个振荡(由于 向通常要求周期性,故没有非振荡解),只是角向振荡。
向通常要求周期性,故没有非振荡解),只是角向振荡。
在球坐标系中, 的解是球贝塞尔函数,意义和柱坐标系下类似。
的解是球贝塞尔函数,意义和柱坐标系下类似。 仍旧具有
仍旧具有 形式的解(同样有周期性要求)。
形式的解(同样有周期性要求)。 描述了
描述了 方向的振荡,只不过具体数学形式比较复杂(涉及勒让德函数)。“球谐函数”就是
方向的振荡,只不过具体数学形式比较复杂(涉及勒让德函数)。“球谐函数”就是 。
。
球坐标系:![]() ,3D图:
,3D图:
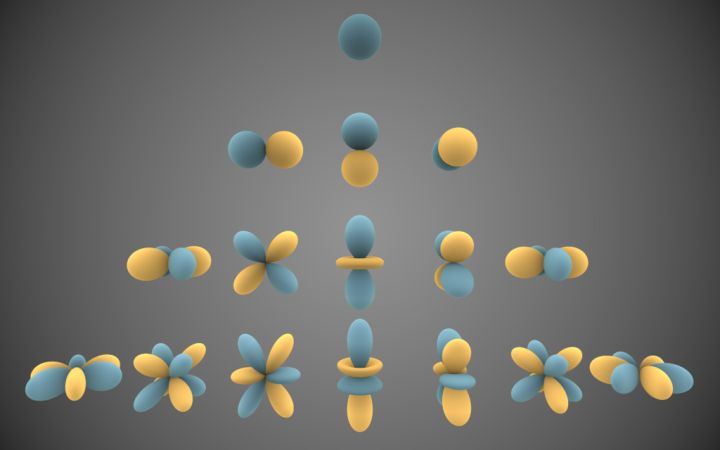
2D密度图:
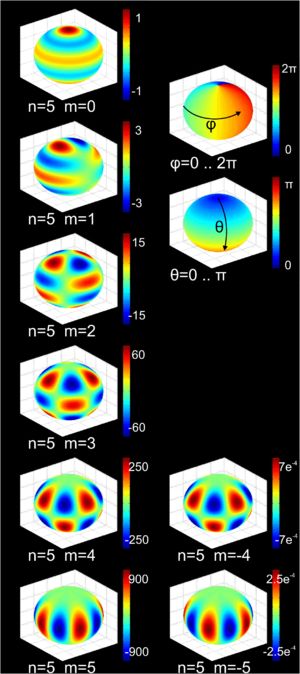
最后,上面出现的各种函数都有各自的正交完备性,类似于三角函数的正交完备性。所以可以用来展开其他函数,正如傅里叶变换。