Machine Learning Notes PartⅢ

前言：由于本人今年考研结束后才开始接触ML，入门决定从Andrew Ng的ML课程学起。笔记内容主要来自Andrew Ng教授的讲义和学习视频，以及在学习过程中翻阅的资料，顺序大致按照网易云课堂上的目录，大多是自己觉得有意义的或者难懂的内容，然而其中难免掺杂自己的理解，如有错误，敬请大家批评指正。

六 逻辑回归(Logistic Regression)

---

分类问题 （Classification）

分类问题中，要预测的值y是离散的值，此时要用到逻辑回归（Logistic Regression），这是目前十分流行的一种算法。
通常，预测的结果是是否属于某一个类，例如：判断一封电子邮件是否是垃圾邮件；判断一次金融交易是否是欺诈；判断肿瘤是否是良性还是恶性。
我们将因变量（Dependent Variable）可能属于的两个类分别称为负向类（Negative Class）和正向类（Positive Class），则因变量$y\in(0,1)$,其中0表示负向类，1表示正向类。


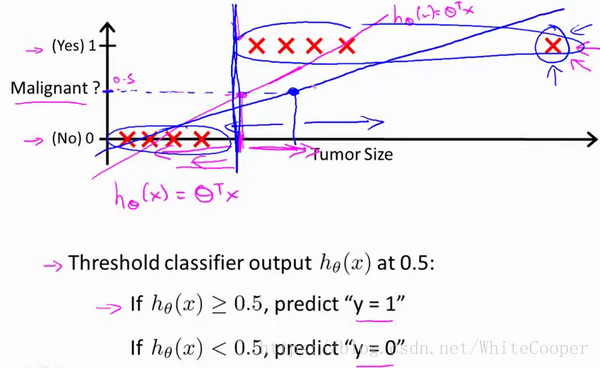
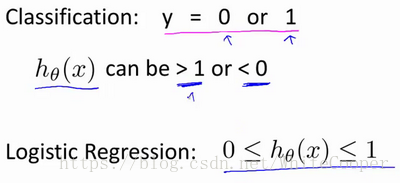
如果我们要用线性回归算法来解决一个分类问题，对于分类， 取值为 0 或者1，但如果你使用的是线性回归，那么假设函数的输出值可能远大于 1，或者远小于0，即使所有训练样本的标签 都等于 0 或 1。尽管我们知道标签应该取值0 或者1，但是如果算法得到的值远大于1或者远小于0的话，就会感觉很奇怪。所以我们在接下来的要研究的算法就叫做逻辑回归算法，这个算法的性质是：它的输出值永远在0到 1 之间。
顺便说一下，逻辑回归算法是分类算法，我们将它作为分类算法使用。有时候可能因为这个算法的名字中出现了“回归”使你感到困惑，但逻辑回归算法实际上是一种分类算法，它适用于标签 取值离散的情况，如：1 0 0 1。

---

假说表示（Hypothesis Representation）

逻辑回归的输出变量范围一直在0和1之间，其模型假设是：$h_\theta(x) = g(\theta^\mathrm TX)$,其中X代表特征向量，$h_\theta(x)$的作用是对于给定的输入变量x，根据选择的参数$\theta$，计算输出变量y=1的可能性（Estimated Probablity）即$h_\theta(x) = p(y=1|x;\theta)$，g代表逻辑函数（Logistic Function），是一个常用的S型逻辑函数（SIgmoid Function），公式为：$g(z) = {\frac {1}{1+e^{-z}}}$
函数图像为：

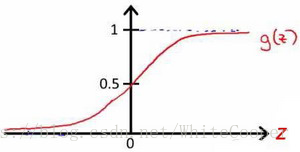
例如，对于给定的输入x通过已经得到的参数$\theta$计算得出$h_\theta(x)$=0.7,则表示由70的概率y为正向类，相对的，就有1-$h_\theta(x)$=1-0.7=0.3即30%的概率为负向类。

---

判定边界（Decision Boundary）

判定边界这个概念可以帮助我们更好的理解假设函数到底在做些什么。
回顾一下模型的假设：模型假设是：$h_\theta(x) = g(\theta^\mathrm TX)$,其中X代表特征向量，$h_\theta(x)$的作用是对于给定的输入变量x，根据选择的参数$\theta$，计算输出变量y=1的可能性（Estimated Probablity）即$h_\theta(x) = p(y=1|x;\theta)$，g代表逻辑函数（Logistic Function），是一个常用的S型逻辑函数（SIgmoid Function），公式为：$g(z) = {\frac {1}{1+e^{-z}}}$
从上面的g（z）函数图像结合假设函数可以看出：
当z=0时，g(z)=0.5,此时$h_\theta(x) = 0.5$
当z<0时，g(z)$\in$(0,0.5),$h_\theta(x) \in(0,0.5)$,预测y值为0
当z>0时，g(z)$\in$(0.5,1),$h_\theta(x) \in(0.5,1)$,预测y值为1
又$\theta^\mathrm TX=z$,所以当$\theta^\mathrm TX$>=0时，预测y=1;当$\theta^\mathrm TX$<0时,预测y=0
现在假设有一个模型：

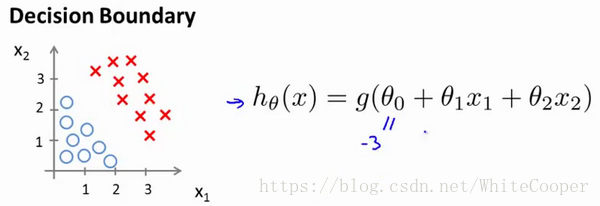
假设参数$\theta$是向量[-3,1,1]， 则当$-3+x_1+x_2\geq0$时，模型将预测 y=1。 我们可以绘制直线$x_1+x_2=3$，这条线便是我们模型的分界线，将预测为1的区域和预测为 0的区域分隔开。
划分后的图形如下：

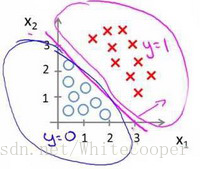
以上只是一次方情况，还可以用二次方、三次方等，也就是所我们可以用非常复杂的模型来适应非常复杂形状的判定边界。

---

代价函数（Cost Function）

对于线性回归模型，我们定义的代价函数是所有模型误差的平方和。理论上来说，我们也可以对逻辑回归模型沿用这个定义，但是问题在于，当我们将$h_\theta(x)={\frac{1}{1+e^{-{\theta ^ \mathrm T}X}}}$带入到这样定义了的代价函数中时，我们得到的代价函数将是一个非凸函数（non-convexfunction）。

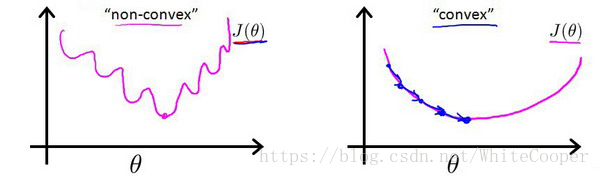
通过这个非凸函数可以看出，存在许多的局部最小值，很影响梯度下降算法寻找最优的局部最小值。
线性回归的代价函数为$J(\theta)=\frac{1}{m}\sum_{i=1}^{m}\frac{1}{2}({h_\theta(x^{(i)})-y^{(i)})^2}$
同理可以定义逻辑函数的代价函数为：$J(\theta)=\frac{1}{m}\sum_{i=1}^{m}Cost(h_\theta(x^{(i)},y^{(i)}))$,其中，

$$Cost(h_\theta(x^{(i)},y^{(i)}) = \begin{cases} -\log(h_\theta(x)), & \text{if y = 1} \\ -\log(1-h_\theta(x)), & \text{if y = 0} \end{cases}$$
$h_\theta(x)与Cost(h_\theta(x^{(i)},y^{(i)})$之间的关系如下图所示：

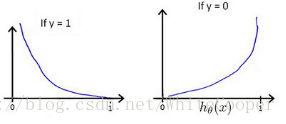
可以看出，当y=1时，如果 $h_\theta(x)$也为1，那么此时误差为0，如果 $h_\theta(x)$不为1，随着 $h_\theta(x)$减小，误差增大。
当y=0时，如果 $h_\theta(x)$也为0，那么此时误差为0，如果 $h_\theta(x)$不为0，随着 $h_\theta(x)$增大，误差增大。
将构建的Cost函数简化后，得到 $Cost(h_\theta(x),y)=-y\times\log(h_\theta(x))-(1-y)\times \log(1-h_\theta(x))$
带入代价函数得到： $J(\theta)=-\frac{1}{m}\sum_{i=1}^{m}{[y^{(i)}\log(h_\theta(x^{(i)}))+(1-y^{(i)})\log(1-h_\theta(x^{(i)}))]}$

在得到这样一个代价函数以后，我们便可以用梯度下降算法来求得能使代价函数最小的参数了。
算法为：
Repeat{
$\theta_j:=\theta_j-\alpha\frac{\partial}{\partial\theta_j}J(\theta)$
（Simultaneously update all $\theta_j$）
}
求导后得到：
Repeat{
$\theta_j:=\theta_j-\alpha\frac{1}{m}\sum_{i=1}^{m}[h_\theta(x^{(i)})-y^{(i)}]x_j^{(i)}$
（Simultaneously update all $\theta_j$）
}

注：虽然得到的梯度下降算法表面上看上去与线性回归的梯度下降算法一样，但是这里的$h_\theta(x)=g(\theta^\mathrm TX)$与线性回归中不同，所以实际上是不一样的。另外，在运行梯度下降算法之前，进行特征缩放依旧是非常必要的。
一些梯度下降算法之外的选择： 除了梯度下降算法以外，还有一些常被用来令代价函数最小的算法，这些算法更加复杂和优越，而且通常不需要人工选择学习率，通常比梯度下降算法要更加快速。这些算法有：共轭梯度（Conjugate Gradient），局部优化法(Broyden fletcher goldfarb shann,BFGS)和有限内存局部优化法(LBFGS).

---

多类别分类：一对多（Multiclass Classification_ One-vs-all）

上面我们讲的都是而分类问题，现在看一下多分类问题。
比如：假如说你现在需要一个学习算法能自动地将邮件归类到不同的文件夹里，或者说可以自动地加上标签，那么，你也许需要一些不同的文件夹，或者不同的标签来完成这件事，来区分开来自工作的邮件、来自朋友的邮件、来自家人的邮件或者是有关兴趣爱好的邮件，那么，我们就有了这样一个分类问题：其类别有四个，分别用y=1、y=2、y=3、y=4 来代表。
对于之前的二分类问题，可能图像是这样：

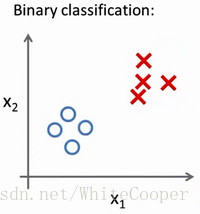
然而对于多文类问题，图像可能就是这样：

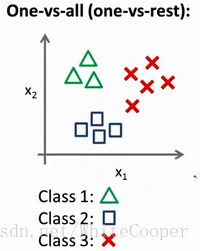
现在我们有一个训练集，好比上图表示的有3个类别，我们用三角形表示y=1 ，方框表示y=2，叉叉表示y=3 。我们下面要做的就是使用一个训练集，将其分成3个二元分类问题。
我们先从用三角形代表的类别1开始，实际上我们可以创建一个，新的”伪”训练集，类型2和类型3定为负类，类型1设定为正类，我们创建一个新的训练集，如下图所示的那样，我们要拟合出一个合适的分类器。

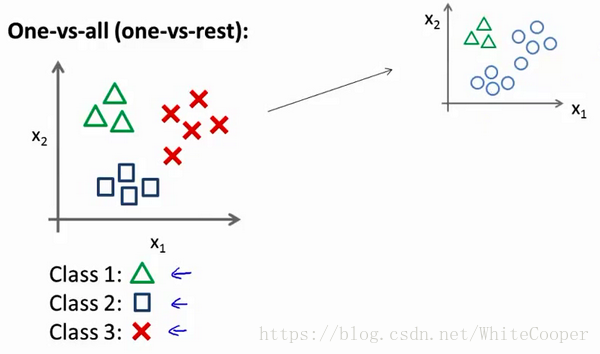
这里的三角形是正样本，而圆形代表负样本。可以这样想，设置三角形的值为1，圆形的值为0，下面我们来训练一个标准的逻辑回归分类器，这样我们就得到一个正边界。
为了能实现这样的转变，我们将多个类中的一个类标记为正向类（y=1），然后将其他所有类都标记为负向类，这个模型记作$h_\theta^{(1)}(x)$。接着，类似地第我们选择另一个类标记为正向类（y=2），再将其它类都标记为负向类，将这个模型记作$h_\theta^{(2)}(x)$ ,依此类推。
最后我们得到一系列的模型简记为$h_\theta^{(i)}(x)=p(y=i|x;\theta)$： 其中:i=(1,2,3…,k)

最后，在我们需要做预测时，我们将所有的分类机都运行一遍，然后对每一个输入变量x，然后我们选择能够一个让$h_\theta^{(i)}(x)$最大的i。

---

---

七 正则化（Regulazation）

---

过拟合（Overfitting）

如果我们有非常多的特征，我们通过学习得到的假设可能能够非常好地适应训练集（代价函数可能几乎为0），但是可能会不能推广到新的数据。下图是一个回归问题的例子：

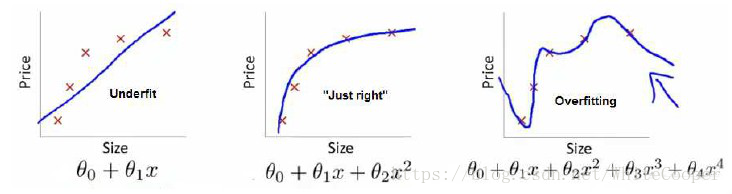
第一个模型是一个线性模型，欠拟合，不能很好地适应我们的训练集；第三个模型是一个四次方的模型，过于强调拟合原始数据，而丢失了算法的本质：预测新数据。我们可以看出，若给出一个新的值使之预测，它将表现的很差，是过拟合，虽然能非常好地适应我们的训练集但在新输入变量进行预测时可能会效果不好；而中间的模型似乎最合适。
分类问题中也存在这样的问题：

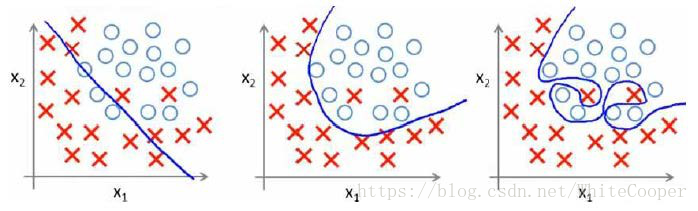
就以多项式理解，x的次数越高，拟合的越好，但相应的预测的能力就可能变差。
问题是，如果我们发现了过拟合问题，应该如何处理？
1.丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征，或者使用一些模型选择的算法来帮忙（例如PCA）
2.正则化。 保留所有的特征，但是减少参数的大小（magnitude）。

代价函数（Cost Function）

正则化的基本方法就是在一定程度上减小参数$\theta$的值。然而大多时候特征都很多，我们并不知道其中哪些特征我们要惩罚，我们将对所有的特征进行惩罚，并且让代价函数最优化的软件来选择这些惩罚的程度。这样的结果是得到了一个较为简单的能防止过拟合问题的假设：$J(\theta)=\frac{1}{2m}\sum_{i=1}^{m}[\frac{1}{2}({h_\theta(x^{(i)})-y^{(i)})^2}+\lambda\sum_{j=1}^{n}\theta_j^2]$
其中又称为正则化参数（Regularization Parameter）。 注：根据惯例，我们不对 进行惩罚。经过正则化处理的模型与原模型的可能对比如下图所示：

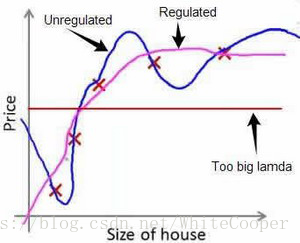
如果我们令$\lambda$的值很大的话，为了使Cost Function 尽可能的小，所有的$\theta$的值（不包括$\theta_0$）都会在一定程度上减小。
但若λ的值太大了，那么$\theta$的值（不包括$\theta_0$）都会趋近于0，这样我们所得到的只能是一条平行于轴的直线。
所以对于正则化，我们要取一个合理的 的值，这样才能更好的应用正则化。

---

正则化线性回归（Regularized Linear Regression）

对于线性回归的求解，我们之前推导了两种学习算法：一种基于梯度下降，一种基于正规方程。
正则化线性回归的代价函数为：$J(\theta)=\frac{1}{2m}\sum_{i=1}^{m}[\frac{1}{2}({h_\theta(x^{(i)})-y^{(i)})^2}+\lambda\sum_{j=1}^{n}\theta_j^2]$
对于$\theta_j$（除$\theta_0$外）令代价函数最小化，用梯度下降法可以得到：
$\theta_j:=\theta_j(1-\alpha\frac{\lambda}{m})-\alpha\frac{1}{m}\sum_{i=1}^{m}[h_\theta(x^{(i)})-y^{(i)}]x_j^{(i)}$
可以看出，正则化线性回归的梯度下降算法的变化在于，每次都在原有算法更新规则的基础上令值减少了一个额外的值。
我们同样也可以利用正规方程来求解正则化线性回归模型，方法如下所示：

$$\theta = \left( X^\mathrm TX+\lambda \begin{bmatrix} 0 &&&& \\ & 1&&& \\&&1&&\\&&&\ddots&\\&&&&1 \end{bmatrix} \right)^{-1}X^\mathrm Ty$$
图中，矩阵为（n+1）*（n+1）维。

---

正则化逻辑回归（Regularized Logistic Regression）

现在我们用梯度下降的方法优化逻辑回归代价函数

同样的，我们给这个代价函数也增加一个正则化的表达式，得到新的代价函数：$J(\theta)=-\frac{1}{m}\sum_{i=1}^{m}{[y^{(i)}\log(h_\theta(x^{(i)}))+(1-y^{(i)})\log(1-h_\theta(x^{(i)}))]}+\frac {\lambda}{2m}\sum_{j=1}^{n}\theta_j^2$
对于$\theta_j$（除$\theta_0$外）令代价函数最小化，用梯度下降法可以得到：
$\theta_j:=\theta_j(1-\alpha\frac{\lambda}{m})-\alpha\frac{1}{m}\sum_{i=1}^{m}[h_\theta(x^{(i)})-y^{(i)}]x_j^{(i)}$
*注：①看上去同线性回归一样，但是$h_\theta(x)=g(\theta^\mathrm TX)$，所以与线性回归不同。
②$\theta_0不参与任何一个正则化$ *