<更新提示>
<第一次更新>
<正文>
图论
图论〔Graph Theory〕是数学的一个分支。它以图为研究对象。图论中的图是由若干给定的点及连接两点的线所构成的图形,这种图形通常用来描述某些事物之间的某种特定关系,用点代表事物,用连接两点的线表示相应两个事物间具有这种关系。
本文主要讲在OI竞赛中的一些图论问题及图论算法。
目录
·图的基本概念<上篇>
·图的储存结构<上篇>
·图的遍历<上篇>
·最短路<上篇>
·最小生成树<下篇>
·拓扑排序<下篇>
·差分约束系统<下篇>
BEGIN!
图的基本概念
图是由一个顶点的集合V和一个顶点间关系的集合E组成:
记 G=(V,E)
V:顶点的有限非空集合。
E:顶点间关系的有限集合(边集)。
存在一个结点v,可能含有多个前驱结点和后继结点。
无向图:
在图G=(V,E)中,如果对于任意的顶点a,b∈V,当(a,b)∈E时,必有(b,a)∈E(即关系R对称),此图称为无向图。即一个图的边都没有确定的方向,能双向联通。
有向图:
如果对于任意的顶点a,b∈V,当(a,b)∈E时 ,(b,a)∈E未必成立,则称此图为有向图。
在有向图中,通常用带箭头的边连接两个有关联的结点。刚好和无向图相反,每一条边像单行道,不能逆向行驶。
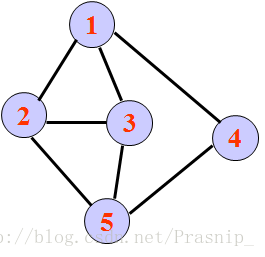
(无向图)
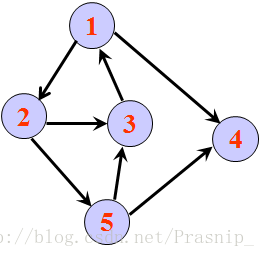
(有向图)
在有向图中:
入度——以该顶点为终点的边的数目和 。
出度——以该顶点为起点的边的数目和 。
度数为奇数的顶点叫做奇点,度数为偶数的点叫做偶点。
度:等于该顶点的入度与出度之和。
结论:图中所有顶点的度=边数的两倍
连通:如果存在一条从顶点u到v有路径,则称u和v是连通的。
连通图:图中任意的两个顶点u和v都是连通的,称为连通图。否则称为非连通图。
带权图:图中的边可以加上表示某种含义的数值,数值称为边的权,此图称为带权图。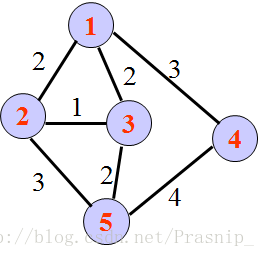
(带权图)
图的储存结构
图是数据结构中的一种,但因为里面涉及了大量算法和较困难的问题,所以单独分开。因为图是数据结构的一种,所以我们首先要将图进行存储。
常用的储存结构有三种
1 邻接矩阵
2 邻接表
3 边表
邻接矩阵
邻接矩阵就是用一个二维数组来存储,a[i][j]代表的意义就是从节点i到节点j是否有边相连,在无向图中,1代表i,j互相连接,有向图在代表从i到j有单向边相连,反之0就代表没边,如果输一个大于1的数值,就代表这条边的权值是这个数。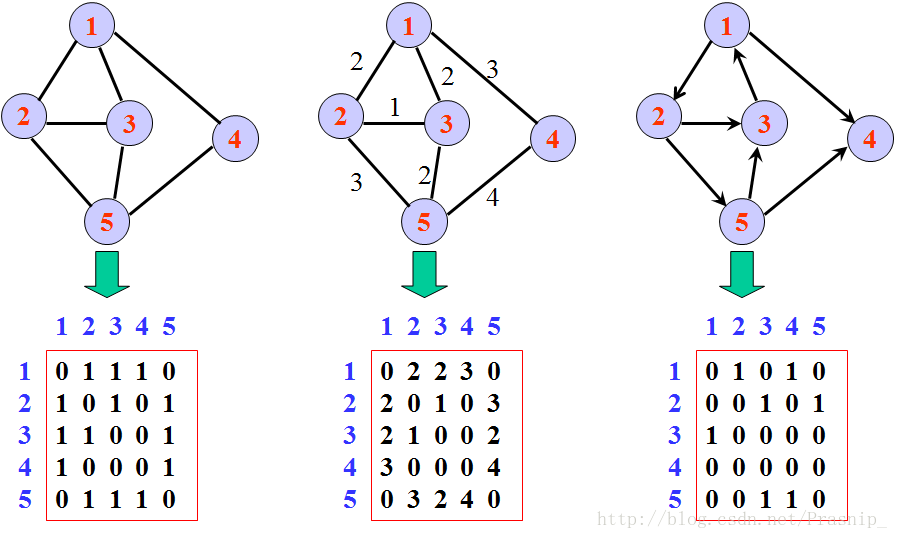
(如图示)
数据的读入方式看具体的题目,一般的读入方式有两种:
1 直接给出邻接矩阵:直接读入(不附代码)
2 给出两个相邻的顶点(及权值):对邻接矩阵用具体的下表进行赋值。
cin>>n>>m;
for(int i=1;i<=n;i++)
{
int x,y,v;
cin>>x>>y>>v;//没权值时赋为1
a[x][y]=v;
//a[y][x]=v;无向图
}邻接表
邻接表就是使用链表来存储图。
结构如下:
无权图:| 节点 | 邻节点指针 |
有权图:| 节点 | 边权值 | 邻节点指针 |
起点表:link[],相当于链表中的储存链表头的数组,表示由i点第一条边出去的下标。
struct edge{
int y,v,next; //y表示这条边的终点编号,v是权值;
}; //next表示同起点下条边的编号是多少
edge e[maxm+10]; //边表。
int linkk[maxn+10]; //起点表 link[i]表示由i出去的第一条边的下标是多少
void insert(int ss,int ee,int vv)//ss为起点,ee为终点,vv为权值。
{
e[++t].y=ee; e[t].v=vv; //t表示有t条边,是个全局变量。
e[t].next=linkk[ss]; linkk[ss]=t;
}
void init(){
scanf("%d %d %d",&n,&p,&m);
for (int i=0;i<m;i++) {
int xx,yy,zz;
scanf("%d%d%d",&xx,&yy,&zz);
insert(xx,yy,zz);
insert(yy,xx,zz); //这里插入的是无向图,所以两条边都要插入。
}
}
邻接矩阵与邻接表的区别:
邻接矩阵:代码书写简单,找邻接点慢
采用二维数组的静态存储结构
一般点数|v|小于 等于5000的时候,用邻接矩阵。
邻接表:代码书写较复杂,找邻接点快
采用动态存储结构(指针或用数组模拟)
一般点数|v|大于等于5000,并且边得个数不是很多的时候,用邻接表,并且现在一般都是用数组来模拟。
稀疏图:边表
struct edge
{
int x,y,v;//两个点以及边权
}e[MAXN]={};图的遍历
图的遍历就是对一个图的每一个节点进行一次有且仅有一次的访问。和搜索遍历的顺序类似,图的遍历也分两种:dfs遍历和bfs遍历。
DFS遍历
遍历算法:
1 从某一起始节点开始,对图进行访问,并对该节点标记:已访问。
2 再从上一个节点的一个邻节点继续作为始节点进行访问,并标记。
3 当始节点的的所有邻节点访问完时,返回到始节点的父节点继续访问,直至所有节点访问完毕
邻接矩阵遍历代码:
void dfs(int k)
{
vis[k]=true;
for(int i=1;i<=n;i++)
{
if((!vis[i])&&(a[k][i]))
dfs(i);
}
}邻接表遍历代码:
void dfs(int k)
{
for(int i=linkk[k];i;i=e[i].next)
{
if(!vis[e[i].y])
{
vis[e[i].y]=1;
dfs(e[i].y);
}
}
}BFS遍历
BFS按层次遍历:
1 从图中某节点出发,访问该节点并标记。
2 按广度优先搜索的顺序遍历该节点的邻节点,标记。
3 直至访问图中的每一个节点。
邻接矩阵遍历代码:
void bfs(int 1)
{
memset(q,0,sizeof(q));
int head=0,tail=1;
q[i]=k;vis[i]=true;
while(head<tail)
{
int k=q[++head];
for(int j=1;j<=n;j++)
{
if(a[k][j]&&!vis[j])
{
q[++head]=j;
vis[j]=true;
}
}
}
}邻接表的遍历代码:
void bfs(int i)
{
int head=0,tail=1;
q[1]=i;
while(head++<=tail)
{
for(int j=linkk[q[head]];j;j=e[j].next)
{
if(!vis[e[j].y])
{
vis[e[j].y]=1;
q[++tail]=e[j].y;
}
}
}
}最短路
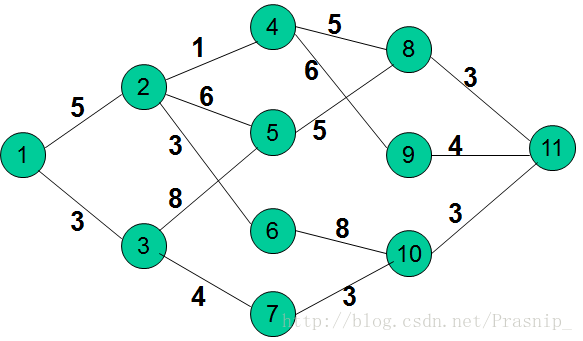
引子:若有图G(若图所示),怎样从节点1到节点11使所走路径总和最短?
即求图论中的最短路径问题。
最短路径的属性
三角形性质
设源点s到x,y的最短路径的长度为dis[x],dis[y],x,y有直接路径且长度为len[x][y],则有以下三角形定理:dis[x]+len[x][y]>=dis[y]。
松弛:若处理过程中,有两点x,y不符合三角形定理,则可以利用三角形定理对嘴短路进行更新,称该操作为松弛:
if(dis[x]+len[x][y]<dis[y])
{
dis[y]=dis[x]+len[x][y];
}对于任意两点之间的最短路径——floyd算法
目标:求出图中任意两点的最短路径dis[i][j]。
原理:图的传递闭包思想:
if(dis[i][k]+dis[k][j]<dis[i][j])
{
dis[i][j]=dis[i][k]+dis[k][j];
}时间复杂度:O(n3)
算法代码:
for(int k=1;k<=n;k++)
{
for(int j=1;j<=n;j++)
{
for(int i=1;i<=n;i++)
{
if(dis[i][k]+dis[k][j]<dis[i][j])
{
dis[i][j]=dis[i][k]+dis[k][j];
}
}
}
}初始化条件:
dis[i][i]=0;//自己到自己的距离为0
dis[i][j]=边权;//i到j有直接相连的边
dis[i][j]=INF;//i到j没有直接相连的边,将其设为正无穷对于一个顶点到其他顶点的最短路径——dijkstra算法
目标:一个源点到其他顶点的最短路径,不允许负权边——单源,非负。
原理:贪心思想
思路:
将点分为两个集合,一开始集合1中只有一个源点,其他点均在集合2中。
1 在集合2中找到一个距离源点最近的顶点,加入集合1。
2 对加入后集合2中的每一个顶点进行松弛操作,即修改在加入顶点k后在集合2中的剩余顶点j经过k后是否变短。
如果变短,修改dis[j]。
3 重复1,直至集合2为空。
时间复杂度:O(n2)
算法代码如下
void dijkstra(int st)
{
for(int i=1;i<=n;i++)dis[i]=a[start][i];
memset(vis,0,sizeof(vis));
vis[start]=1;dis[start]=0;
for(int i=1;i<=n;i++)
{
int min=INF;
int k=0;
for(int j=1;j<=n;j++)
{
if(!vis[j]&&dis[j]<minn)
{
minn=dis[j];
k=j;
}
}
if(k==0)return;
vis[k]=1;
for(int j=1;j<=n;j++)
{
if(!vis[j]&&dis[k]+a[k][j]<dis[j])
{
dis[j]=dis[k]+a[k][j];
}
}
}
}初始化条件:
dis[start]=0;//起始点为0
dis[j]=a[start][j];//有边相连,直接赋为边权无边设为INF对于单源点最短路,可以判断负环的算法——Bellman—ford算法
引子:容易得知,当图中有负权边构成的回路时,dijkstra算法求的最短路是错的,只会求出负无穷的答案,所以我们需要一种判断负环的算法。
目标:判断负环。
原理:通过求最短路的松弛次数判断
思路:
1 初始化每一个到源点s的距离为正无穷
2 取所有边(x,y),看x能否对y松弛(由于需要用到取边操作,所以我们用边表存图)
3 没有松弛则return,若有松弛,且松弛次数小于n转 2
4 如果松弛了n次还能松弛,则存在负环
时间复杂度:O(N*E)
算法代码如下:
void bellman_ford(int st)
{
memset(dis,10,sizeof(dis));
dis[st]=0;
bool re=0;
for(int i=1;i<=n;i++)
{
re=0;
for(int j=1;j<=m;j++)
{
if(dis[a[j].x]+a[j].v<dis[a[j].y])//松弛
{
dis[a[j].y]=dis[a[j].x]+a[j].v;
re=1;
}
}
if(!re)return 0;//不存在负环
}
return 1;//超过n次松弛,存在负环
}对于Bellman—ford算法迭代的优化——SPFA算法
引子:Bellman—ford算法中,如果边(x,y)在上一次dis[x]没有改变,那么显然下一次检查也是多余的。
改进思路:我们只要在迭代时只检查刚松弛过的点x能不能在松弛其他点即可。就可以利用BFS的队列来实现了,每一次将松弛的点加入队列,在不断从队头取出点松弛其他的点即可。(用邻接表实现)
时间复杂度:O(K*E)
算法代码如下:
void spfa(int st)
{
memset(dis,10,sizeof(dis));
memset(vis,0,sizeof(vis));
dis[st]=0;vis[st]=1;q[1]=st;
//vis数组标记的是是否在队列中
int head=0,tail=1;
while(head<tail)
{
int temp=q[++head];
vis[temp]=0;
for(int i=linkk[temp];i;i=e[i].next)
{
int Next=e[i].y;
if(dis[temp]+e[i].v<dis[Next])
{
dis[Next]=dis[temp]+e[i].v;
if(!vis[Next])
{
q[++tail]=Next;
vis[Next]=1;
}
}
}
}
}<后记>图论大工程上篇到此结束啦
<废话>