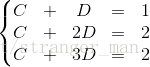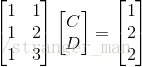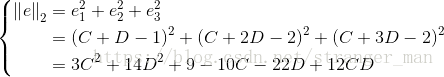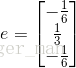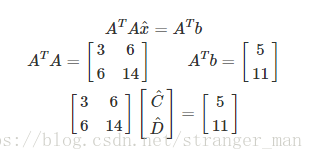10投影矩阵和最小二乘

转载自：https://blog.csdn.net/huang1024rui/article/details/69568991

上一讲中，我们知道了投影矩阵$P=A(A^{T}A)^{-1}A^{T}$，$Pb$将会把向量投影在A的列空间中。即只要知道矩阵$A$的列空间，就能得到投影矩阵$P$。

1.投影矩阵（Ax=b无解的情形）

1.1两个极端的例子：

1) 如果$b∈C(A)$，则$Pb=b$；
2) 如果$b⊥C(A)$，则$Pb=0$。

证明1):

$$Pb = A(A^TA)^{-1}A^{T}b=A(A^{T}A)^{-1}A^{T}Ax=A((A^{T}A)^{-1}A^{T}A)x=Ax=b$$

证明2):

$$Pb = A(A^TA)^{-1}A^{T}b=A(A^{T}A)^{-1}(A^{T}b)=A(A^{T}A)^{-1}0=0$$

具体的图示化看下文：

1.2一般情形

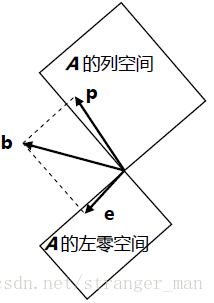
一般情况下，$b$将会有一个垂直于$A$的分量，有一个在$A$列空间中的分量，投影的作用就是去掉垂直分量而保留列空间中的分量。

向量$b$投影后，有$b=e+p,p=Pb,e=(I−P)b$，这里的$p$是$b$在$C(A)$中的分量，而$e$是$b$在$N(A^T)$中的分量。

可以理解为：向量$b$的投影在$A$的列空间，偏差向量的投影在左零空间上，我们知道$P$，可以将$b$投影到$p$，那么一个什么样的投影矩阵把$b$投影到了$e$？因为列空间与左零空间正交补，所以他们共同组成了整个空间，$I$的列空间就是整个空间，$I−P$就是把$b$投影到$e$的矩阵。

2. 最小二乘法（Ax=b）

回到上一讲最后提到的例题：

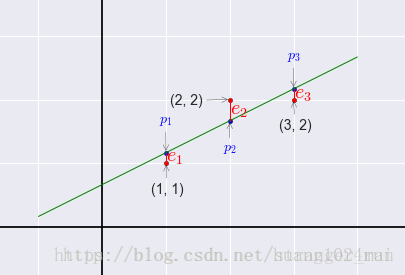
我们需要找到距离图中三个点$(1,1),(2,2),(3,2)$ ,偏差最小的直线：$y=C+Dt$。

根据条件可以得到方程组:
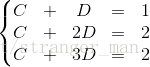，写作矩阵形式: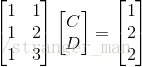,也就是我们的$Ax=b$，很明显方程组无解。

此时我们要找到最接近的解”最优解”，我们要使得解最优即误差最小，定义误差为$Ax−b=e$的模长的平方即$∥Ax−b∥^2=∥e∥^2=e^2_{1}+e^2_{2}+e^2_{3}$。此处使用平方的原因一是排除开根号带来的非线性运算，一是方便利用偏导数求解最小值。

2.1利用偏导

这里如果使用偏导数我们也能得到关于最优解的方程，展开结果为:

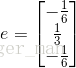然后对$C$求偏导为$6C−10+12D=0$；对D求偏导为$28D−22+12C=0$。 解方程得$\hat{C}=\frac{2}{3},\hat{D}=\frac{1}{2}$,则“最佳直线”为$y=\frac{2}{3}+\frac{1}{2}t$，则“最佳直线”为y=23+12t，带回原方程组解得$p_1=\frac{7}{6},p_2=\frac{5}{3},p_3=\frac{13}{6}$，即$e_1=-\frac{1}{6},e_2=\frac{1}{3},e_3=-\frac{1}{6}$。 最终得到：$p=\begin{bmatrix}\frac{7}{6}\\ \frac{5}{3}\\ \frac{13}{6}\end{bmatrix}$ ,,易看出$b=p+e$，同时我们发现$p⋅e=0$即$p⊥e$。可以验证，向量$p$与$e$ 正交，并且$e$ 与矩阵$A$的列空间正交。

可以验证，向量$p$ 与$e$ 正交，并且$e$ 与矩阵$A$ 的列空间正交。

$$p^Te=7/6∗(−1/6)+5/3∗1/3+13/6∗(−1/6)=0$$
$$e^Ta1=1∗(−1/6)+1∗1/3+1∗(−1/6)=0$$
$$e^Ta2=1∗(−1/6)+2∗1/3+3∗(−1/6)=0$$
误差向量e不仅垂直于投影向量p，它同时垂直于列空间。

2.2利用矩阵

用矩阵的方法求解$A\hat{x}=Pb$得到的方程是一样的，现在我们尝试解出$\hat{x}= \begin{bmatrix}\hat{C}\\ \hat{D}\end{bmatrix},p= \begin{bmatrix}p_1\\ p_2\\p_3\end{bmatrix}$。

3.证明$A^TA$可逆