Definition&Solution

　　线段树是一种log级别的树形结构，可以处理区间修改以及区间查询问题。期望情况下，复杂度为O(nlogn)。

　　　核心思想见百度百科，线段树即将每个线段分成左右两个线段做左右子树。一个线段没有子树，当且仅当线段表示的区间为[a,a]。

　　　由于编号为k的节点的子节点为2k以及2k+1，线段树可以快速的递归左右叶节点。

　　　lazy标记：当进行区间修改的时候，如果一个区间整体全部被包含于要修改的区间，则可以将该区间的值修改后，将lazy标记打在区间上，不再递归左右区间。

　　　例如，要修改[15,30]区间整体+2，当前区间为[16,24]，被包含于要修改的区间。记代表区间[16,24]的节点编号为k，则tree[k]+=2*(24-16+1)，同时lazy[k]+=2。

　　　在下次修改或查询到k节点时，进行lazy的下放，即如下代码

inline void Free(cl l,cl r,cl p) {
    ll m=(l+r)>>1,dp=p<<1;
    tree[dp]+=(m-l+1)*lazy[p];tree[dp+1]+=(r-m)*lazy[p];
    lazy[dp]+=lazy[p];lazy[dp+1]+=lazy[p];
    lazy[p]=0;
}

　　　注意：被打上lazy标记的区间实际上已经修改完区间和，每次free修改的是子区间。

Example

传送门

Description

已知一个数列，你需要进行下面两种操作：

1.将某区间每一个数加上x

2.求出某区间每一个数的和

Input

第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3或4个整数，表示一个操作，具体如下：

操作1：格式：1 x y k 含义：将区间[x,y]内每个数加上k

操作2：格式：2 x y 含义：输出区间[x,y]内每个数的和

Output

输出包含若干行整数，即为所有操作2的结果。

Sample Input

Sample Output

11
8
20

Hint

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=1000，M<=10000

对于100%的数据：N<=100000，M<=100000

Solution

模板题。有一些需要注意的地方会在summary写明

Code

#include<cstdio>
#define maxn 100010
#define maxt 400010
#define ll long long int
#define cl const long long int

inline void qr(long long &x) {
    char ch=getchar();long long f=1;
    while(ch>'9'||ch<'0')    {
        if(ch=='-')    f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')    x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
    x*=f;
    return;
}

inline long long max(const long long &a,const long long &b) {if(a>b) return a;else return b;}
inline long long min(const long long &a,const long long &b) {if(a<b) return a;else return b;}
inline long long abs(const long long &x) {if(x>0) return x;else return -x;}

inline void swap(long long &a,long long &b) {
    long long c=a;a=b;b=c;return;
}

ll n,m,MU[maxn],sign,a,b,c;

ll tree[maxt],lazy[maxt];

void build(const ll l,const ll r,const ll p) {
    if(l>r)    return;
    if(l==r) {tree[p]=MU[l];return;}
    ll m=(l+r)>>1,dp=p<<1;
    build(l,m,dp);build(m+1,r,dp+1);
    tree[p]=tree[dp]+tree[dp+1];
}

inline void Free(cl l,cl r,cl p) {
    ll m=(l+r)>>1,dp=p<<1;
    tree[dp]+=(m-l+1)*lazy[p];tree[dp+1]+=(r-m)*lazy[p];
    lazy[dp]+=lazy[p];lazy[dp+1]+=lazy[p];
    lazy[p]=0;
}

inline void wohenlan(cl l,cl r,cl p,cl v) {tree[p]+=(r-l+1)*v;lazy[p]+=v;}

void add(cl l,cl r,cl p,cl aiml,cl aimr,cl v) {
    if(l>r) return;
    if(l>aimr||r<aiml) {return;}
    if(l>=aiml&&r<=aimr) {wohenlan(l,r,p,v);return;}
    Free(l,r,p);
    ll m=(l+r)>>1,dp=p<<1;
    add(l,m,dp,aiml,aimr,v);add(m+1,r,dp+1,aiml,aimr,v);
    tree[p]=tree[dp]+tree[dp+1];
}

ll ask(cl l,cl r,cl p,cl aiml,cl aimr) {
    if(l>r) return 0;
    if(l>aimr||r<aiml) {return 0;}
    if(l>=aiml&&r<=aimr) {return tree[p];}
    Free(l,r,p);
    ll m=(l+r)>>1,dp=p<<1;
    return ask(l,m,dp,aiml,aimr)+ask(m+1,r,dp+1,aiml,aimr);
}

int main() {
    qr(n);qr(m);
    for(int i=1;i<=n;++i) qr(MU[i]);
    build(1ll,n,1ll);
    while(m--) {
        sign=a=b=0;qr(sign);qr(a);qr(b);
        if(sign==1) {
            c=0;qr(c);
            add(1,n,1,a,b,c);
        }
        else printf("%lld\n",ask(1, n, 1, a, b));
    }
    return 0;
}

Summary

　　1、线段树大小要开4*n。理论上线段树会有2*n个子节点，但是试试这棵线段树：1 2 3 4 5

　　　　　　如图所示：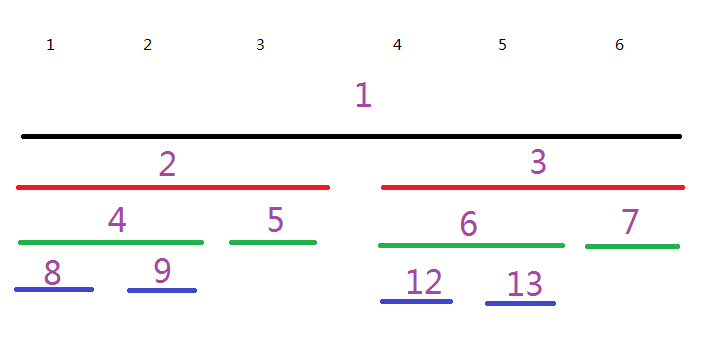

　　　　　　　　　可以看到，节点数确实是6*2-1=11个，但是由于我们每个节点编号都严格按照母节点*2(+1)进行编号，所以我们的编号开到了2*n之外。开4*n是比较保险的。

　　　　2、注意对lazy标记的free操作要在确定区间可以再分以后进行。即先写

if(l>=aiml&&r<=aimr) {wohenlan(l,r,p,v);return;}

　　　　　　或

if(l>=aiml&&r<=aimr) {return tree[p];}

　　　　　　后，如果没有return，则证明区间一定是可再分的，即还没有递归到叶节点，这时才可以进行free操作。否则的话考虑在叶节点的编号可能大于2*n，我们在叶节点free了一下，标记被下放到了4*n以外……

　　　　　　然后你就炸了。

【线段树】【P3372】模板-线段树