本章包含一些自己的理解, 如有偏差还望指出. 本章也是整个系列最重要的一章, 请耐心阅读.
关于IEEE754标准中浮点数的精度是怎么计算的, 网上的资料众说纷纭, 有些还彼此冲突, 我也看的很头大...这里仅分享两种个人觉得比较靠谱的说法.
一. 先说结论
打开IEEE754的维基百科,可以看到其中标注着, 单精度浮点数的精度是"Approximately 7 decimal digits"

有人把这句话翻译为 "大约7位小数" , 把"decimal"翻译成了"小数".
但个人理解, 这里 "decimal的" 含义应该是 "十进制的" , 即32位浮点数的精度是 "大约7位十进制数" , 后文会说为什么这样理解.
二. 在讨论之前...
我们先来思考这样一件事: 现在的计算机能存储[1,2]之间的所有小数吗?
稍想一下就知道: 不可以. 因为计算机的内存或硬盘容量是有限的, 而1到2之间小数的个数是无限的.
极端一点, 计算机甚至无法存储1到2之间的某一个小数, 比如对于小数 1.00000.....一万亿个零.....00001, 恐怕很难用计算机去存储它...
不过计算机却能存储[1, 10000]之间的所有整数. 因为整数是"离散"的, [1, 10000]之间的整数只有10000个. 10000种状态, 很容易就能存储到计算机中, 而且还能进行运算, 比如计算10000 + 10000, 也只是要求你的计算机能存储20000种状态而已...
这样来看的话: 计算机可以进行数学概念中的整数运算的, 但却难以进行数学概念中的小数运算. 小数这种"连续"的东西, 当前的计算机很难应对...
事实上, 计算机为了进行小数运算, 不得不将小数也当成"离散"的值, 一个一个的, 就像整数那样:
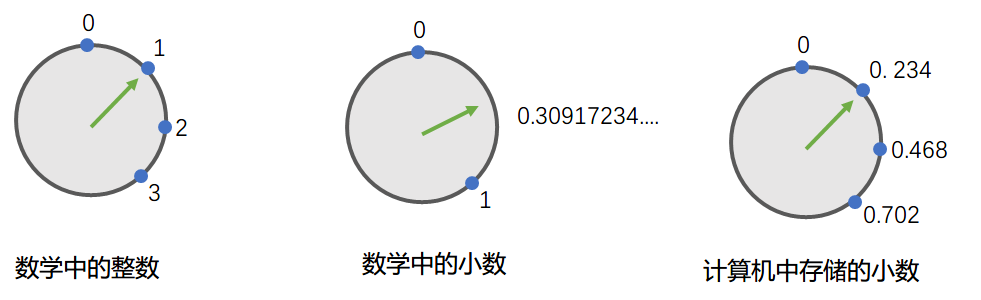
↑ 数学中的整数是一个一个的, 想象绿色指针必须一次走一格
↑ 数学中的小数是连续的, 想象绿色指针可以无极调节, 想走到哪儿走到哪儿
↑ 计算机中存储的小数是一个一个的, 绿色指针必须一次走一格, 就像整数那样
这就引发了精度的问题, 比如上图中, 我们无法在计算机中存储0.3, 因为绿色指针只能一次走一格, 要么在0.234, 要么就到了0.468...
当然, 我们也可以增加计算机存储小数的精度, 或者说缩小点与点之间的间隔:

IEEE754中的单精度浮点数和双精度浮点数大体也是如此: 双精度浮点数中的蓝色小点更密集...
三. 理解角度1: 从"间隔"的角度理解
1. 铺垫
从"间隔"的角度理解来"精度", 其实是这样一种思路:
想象一个类似于上图的圆形表盘, 表盘上有一些蓝点作为刻度, 有一个绿色的指针用于指向蓝点, 绿色指针只能一次走一格: 即只能从当前蓝点移动到下一个蓝点. 不能指向两个蓝点之间的位置.
假如表盘上用于表示刻度的蓝点如下所示:
0.0000
0.0012
0.0024
0.0036
0.0048
0.0060
0.0072
0.0084
0.0096
0.0108
0.0120 (注意这里, 前一个数是108, 这个数是120, 先记住这一点)
0.0132
0.0144
...
即, 这是一组十进制数, 这组数以 0.0012 的步长逐渐递增... 假设这个表盘就就是你的计算机所能表示的所有小数.

表盘示意图
问: 我们能说这个表盘, 或者说这组数的精度达到了 4 位十进制数吗(比如, 可以精确到1位整数 + 3位小数)?
分析: 如果说可以精确点1位整数 + 3位小数, 那我们就应该可以说出下面这样的话:
我们可以说, 当前指针正位于0.001x: 而指针确实可以位于0.0012, 属于0.001x (x表示这一位是任意数, 或说这对该位的精度不做限制)
我们可以说, 当前指针位于0.002x: 而指针确实可以位于0.0024, 属于0.002x
我们可以说, 当前指针位于0.003x: 而指针确实可以位于0.0036, 属于0.003x
...
我们可以说, 当前指针位于0.009x: 而指针确实可以位于0.0096, 属于0.009x
我们可以说, 当前指针位于0.010x: 而指针确实可以位于0.0108, 属于0.010x
我们可以说: 当前指针位于0.011x...但, 注意, 指针始终无法指向0.011x...在我们的表盘中, 指针可以指向0.0108, 或指向0.0120, 但始终无法指向0.011x
...
这就意味着: 对于当前表盘 (或者说对于这组数) 来说, 4位精度太高了...4位精度所能描述的状态中, 有一些是无法用这个表盘表示的.
那, 把精度降低一些.
我们能说这个表盘, 或者说这组数的精度达到了 3 位十进制数吗(比如, 可以精确到1位整数 + 2位小数)?
再来分析一下: 如果说可以精确点1位整数 + 2位小数, 那我们就应该可以说出下面这样的话:
我们可以说, 当前指针位于0.00xx: 而指针确实可以位于0.0012, 0.0024, 0.0036...0.0098, 这些都属于0.00xx
我们可以说, 当前指针位于0.01xx: 而指针确实可以位于0.0108, 0.0120...这些都属于0.01xx
...
可以看出, 对于当前这个表盘 (或者说对于这组数) 来说, 它完全能"hold住"3位精度. 或者说3位精度所能描述的所有状态在该表盘中都可以得到表示.
如果我们的机器使用这个表盘作为浮点数的取值表盘的话, 那我们就可以说:
我们机器的浮点数精度 (或者说这个表盘的浮点数精度), 能精确到3位十进制数(无法精确到4位十进制数).
而这个精度, 本质上是由表盘间隔决定的, 本例中的表盘间隔是0.0012, 如果把表盘间隔缩小到0.00000012, 那相应的表盘能表示的精度就会提升(能提升到 7 位十进制数, 无法达到 8 位十进制数)
通过这个例子, 希望大家能够直观的认识到 "表盘的间隔" 和 "表盘的精度" 之间, 存在着密切的关系. 这将是后文进行讨论的基础.
事实上: ieee754标准中的32位浮点数, 也可以被想象为一个 "蓝点十分密集的浮点数表盘", 如果我们能分析出这个表盘中蓝点之间的间隔, 那我们就能分析出这个表盘的精度.
注: 也可以用一句很简单的话来解释本小节的例子: 假设浮点数表盘能提供4位精度控制, 比如能控制到1位整数+3位小数, 这就要求它必须能控制到 0.001 这个粒度, 而 0.001 这个值小于该表盘的实际间隔 0.0012... 所以该表盘不能提供4位精度...
2. 32位浮点数的间隔
那怎么分析32位浮点数的间隔与精度呢, 有一个很笨的方法: 把32位浮点数能表示的所有小数都罗列出来, 计算间隔. 然后分析精度...
呃...我也确实准备用这个比较笨的方法...下面就开始吧...
注: 此处只分析规格数(normal number), 且先不考虑负数情况, 也就是说不考虑符号位为 1 的情况
32位浮点数能表示的最小规格数是 :
0 00000001 00000000000000000000000 (二进制)
(注意, 规格数的指数位最小为 00000001 , 不能为00000000. 这个在本系列的第二章中已经讨论过了, 以下不再赘述)
紧邻的下一个数是:
0 00000001 00000000000000000000001 (二进制)
紧邻的下一个数是:
0 00000001 00000000000000000000010 (二进制)
紧邻的下一个数是:
0 00000001 00000000000000000000011(二进制)
...
这样一步一步的往下走, 223−1 步之后, 我们将指向这个数:
0 00000001 11111111111111111111111(二进制)
再走一步, 也就是2^23步之后, 我们将指向这个数:
0 00000010 00000000000000000000000(二进制)
总结一下: 2^23次移动之后:
我们从起点: 0 00000001 00000000000000000000000,
移动到了终点: 0 00000010 00000000000000000000000
现在可以求间隔了, 间隔 = 差值 / 移动次数 = (终点对应的值 - 起点对应的值) / 2^23,
但是, 先别急着计算. 我们先仔细观察一下, 可以发现, 和起点相比, 终点的符号位和尾数位都没变, 仅仅是指数位变了: 起点指数位00000001 → 终点指数位00000010, 终点的指数位, 比起点的指数位变大了1
而ieee754中浮点数的求值公式是:

(先不考虑符号位)
这样的话: 假如说起点对应的值是
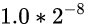
那终点对应的值就应该是
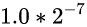
即, 仅仅是指数位变大了1
把指数展开会看的更清晰一些:
假如说起点对应的值是 0.0000 0001 (8位小数)
那终点对应的值就应该是 0.0000 001 (7位小数)
那起点和终点的差值就是: (0.0000 001 - 0.0000 0001), 是一个非常小的数
那间隔就是: 差值 / 2^23
注意: 其实上面我们并没有计算出真正的间隔, 只是假设了起点和终点的值分别是
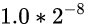
和
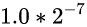
然后算出了一个假设的间隔. 但这个假设格外重要, 下文我们会继续沿用这个假设进行分析 ️
废话不多说, 现在我们继续前进.
现在起点变成了: 0 00000010 00000000000000000000000
再走2^23步, 来到了: 0 00000011 00000000000000000000000
同样: 符号位, 尾数位都没有变, 指数位又变大了1
沿用上面的假设, 此时起点对应的值是
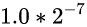
, 则终点对应的值应该是

, 即, 还是指数位变大了1
再次计算差值: 0.0000 01(6位小数) - 0.0000 001(7位小数)
再次计算间隔: 等于 差值 / 2^23(移动次数)
不知道同学们有没有体会到不对劲的地方, 没有的话, 我们计算往前走:
现在起点变成了: 0 00000011 00000000000000000000000
再走2^23步, 来到了: 0 00000100 00000000000000000000000
同理, 终点相对起点, 还只是指数位变大了1
再次计算差值: (0.00001(5位小数) - 0.000001(6位小数))...
再次计算间隔: 等于 差值 / 2^23(移动次数)
感受到不对劲了吗? 继续往前走...
现在起点变成了: 0 00000100 00000000000000000000000
再走2^23步, 来到了: 0 00000101 00000000000000000000000
再次计算差值: (0.0001(4位小数) - 0.00001(5位小数))...
再次计算间隔: 等于 差值 / 2^23(移动次数)
...一路走到这儿, 感受到不对劲了吗?
不对劲的地方在于: 终点和起点的差值! 差值在越变越大! 同理间隔也在越变越大!
不信的话我们来罗列一下之前的差值:
...
那差值就是: 0.0000 001 ( 7位小数) - 0.0000 0001( 8位小数), 差值等于0.0000 0009
...
那差值就是: (0.000001 ( 6位小数) - 0.0000001( 7位小数)), 差值等于0.0000 009
...
那差值就是: (0.00001 ( 5位小数) - 0.000001( 6位小数)), 等于 0.0000 09
...
那差值就是: (0.0001 ( 4位小数) - 0.00001( 5位小数)), 等于 0.0000 9
差值的小数点在不断向右移动, 这样走下次, 总有一天, 差值会变成9, 变成90, 变成90000...
而 移动次数始终 = 2^23, 间隔始终 = 差值/2^23....差值在越变越大, 间隔也会跟着越变越大...
到这里, 你发现了ieee754标准的一个重要特性: 如果把ieee754所表示的浮点数想象成一个表盘的话, 那表盘上的蓝点不是均匀分布的, 而是越来间隔越大, 越来越稀疏:
大概就像这样:
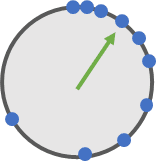
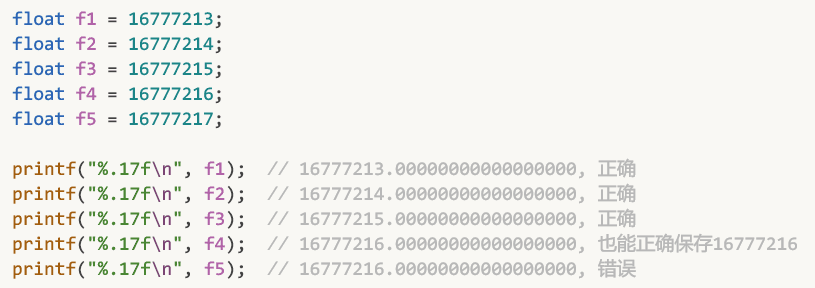
你可以直接在c语言中验证这一特性:

与16777216紧邻的蓝点是16777218, 两数差值为2, 32位浮点数无法表示出16777217
3. 32位浮点数的间隔表
开头我们说过: 知道了表盘的间隔, 就能计算表盘的精度了.
复杂的地方在于, ieee754这个表盘, 间隔不是固定的, 而是越来越大.
幸运的地方在于, wiki已经帮我们总结好了间隔数据:

对于这张表的数据, 我们只关注右侧的三列即可, 它是在告诉我们: [最小值, 最大值]范围间的间隔是多少
比如: 下面这一行告诉我们, 8388608 ~ 16777215这个范围之间的数, 间隔是1

所以32位浮点数可以存储8388608, 也可以存储8388609, 但无法存储8388608.5, 因为间隔是1
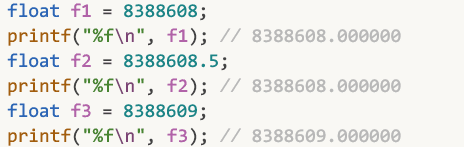
而第二行在说: 1 ~ 1.999999880791这个范围之间的数, 间隔是: 1.19209e-7

去翻一下c语言float.h的源码, 会发现这样一句:
#define FLT_EPSILON 1.192092896e-07F // smallest such that 1.0+FLT_EPSILON != 1.0
↑ 定义常量FLT_EPSILON, 其值为1.192092896e-07F
这个 1.192092896e-07F , 其实就是我们表格中看到的间隔: 1.19209e-7
源码中说: 32位浮点数1.0, 最少也要加上FLT_EPSILON这个常量, 才能不等于1.0.
换句话说, 如果 1.0 加上一个小于 FLT_EPSILON 的数 N, 就会出现1.0 + N == 1.0 这种"诡异的情况".
因为对于 1 ~ 1.999999880791 这个范围中的32位浮点数, 至少要加上 FLT_EPSILON, 或者说至少要加上该范围对应的间隔, 才能够把指针从当前蓝点, 移动到紧邻的下一个蓝点
注意: 如果不是1 ~ 1.999999880791之间的数, 则不一定要加上 1.19209e-7 啊. 准确来说应该是: 某个区间中的数, 至少要加上该区间对应的间隔, 才能从当前蓝点移动到下一个蓝点.
仔细看一看一下上面那张间隔表, 相对你对c语言的浮点数运算会更胸有成竹.
注意: 其实上面的解释中, 存在着一个不大不小的问题. 不过这里先搁置不谈, 等我们理解的更深刻一些时, 再拐回来重新探讨这个问题.
注: 64位浮点数的 间隔表, 也可以参见 IEEE754 WIKI
4. 32位浮点数的精度
那, 为什么说32位浮点数的精度是7位十进制数呢?
首先要说明的是: 32位浮点数的精度是: Approximately 7 decimal digits, 是大约7位十进制数
事实上, 对于有些8位十进制数, 32位浮点数容器也能对其精确保存, 比如, 下面两个数都能精确保存

那所谓的精度是7位十进制数到底是什么意思呢? 探讨这个之前, 我们需要先了解一些更本质的东西
I. 浮点数只能存储蓝点位置对应的值
正如前文所说, 32位浮点数会形成一个表盘, 表盘上的蓝点逐渐稀疏. 绿色指针只能指向某个蓝点, 不能指向两个蓝点之间的位置. 或者换句话说: 32位浮点数只能保存蓝点对应的值.
如果你要保存的值不是蓝点对应的值, 就会被自动舍入到离该数最近的蓝点对应的值. 举例:
在0.5 ~ 1这个范围内, 间隔约为5.96046e-8, 即约为 0.00000005.96046

也就是说: 表盘上有一个蓝点是0.5
下一个蓝点应该是: 当前蓝点 + 间隔 ≈ 0.5 + 0.00000005.96046 ≈ 0.5000000596046
那, 如果我们要保存 0.50000006, 也就是我们要保存的这个值, 稍大于下一个蓝点:
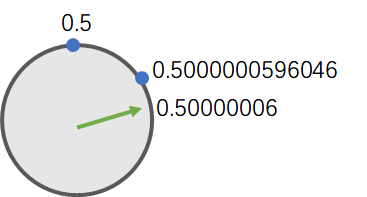
因为绿色指针必须指向蓝点, 不能指向蓝点之间的位置, 所以绿色指针会被"校准"到0.5000000596046, 或者说我们要保存的0.50000006, 会被舍入为0.5000000596046
实测一下:

事实上, 每个32位浮点数容器中, 存储的必然是一个蓝点值
验证一下, 首先求出从0.5开始的蓝点值:
第一个蓝点: 0.5
第二个蓝点: ≈ 0.5 + 0.0000000596046 ≈ 0.5000000596046
第三个蓝点: 第二个蓝点 + 0.0000000596046 ≈ 0.0000001192092
第四个蓝点: 第三个蓝点 + 0.0000000596046 ≈ 0.0000001788138
然后看下面的代码, 发现变量中实际存储的, 其实都是蓝点值:

看打印出来的东西, 可以发现实际存储的都是蓝点值
这是我们需要着重理解的东西
说句题外话, 其实学到现在, 我们就能大体解释一个经典编程问题了: "为什么32位浮点数中的 0.99999999 会被存储为1.0呢", 因为 0.99999999 不是一个蓝点值, 且离他最近的蓝点值是1.0, 然后绿色指针被自动"校准"到了离他最近的蓝点1.0.

II. 理解32位浮点数的精度是7位十进制数
对此我是这样理解的:
例1:
查表, 发现 1024 ~ 2048 范围中的 间隔 约为 0.000122070

如下图: 想要精确存储到小数点后4位, 却发现做不到, 其实只能精确存储到小数点后3位:

试图精确存储到小数点后4位, 却发现实际上无法存储1024.0005, 因为表盘上没有这个1024.0005xxxxxxxx这个级别的数
在这个1024 ~2048这个范围内, 能精确保存的数是 4位十进制整数 + 3位十进制小数 = 7位十进制数
例2:
查表, 发现 8388608 ~ 16777215 范围中的 间隔 为 1
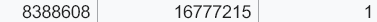
如下图: 想要精确存储到小数点后一位, 却发现做不到, 其实只能精确存储到小数点后零位, 或者说只能精确存储到个位数(因为最小间隔为1):

小数点后一位无法精确存储, 只能精确存储到个位
在这个8388608 ~ 16777215 这个范围内, 能精确保存的数是 7或8位十进制整数 + 0位十进制小数 = 7或8位十进制数
是的, 32位浮点数也能精确保存小于等于 16777215 的 8 位十进制数, 所以说其精度大约是7位十进制数
例3:
查表, 发现 1 ~ 2 范围中的间隔为 1.19209e-7
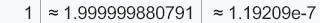
如下图: 想要精确存储到小数点后7位, 却发现做不到, 其实只能精确存储到小数点后6位:

想精确存储到小数点后7位, 却发现实际上无法存储1.0000012, 表盘上没有这个1.0000012xxxx 这个级别的数
在这个1 ~ 2这个范围内, 能精确保存的数是 1位十进制整数 + 6位十进制小数 = 7位十进制数
所谓的32位浮点数的精度是7位十进制数, 大概就是这样算出来的. 基本上 整数位 + 小数位 最多只能有7位, 再多加无法确保精度了 (注意这不是wiki给出的计算方法, wiki给出的算法见下文)
如果你不喜欢这种理解方式, 不妨退一步, 仅记住如下三点即可:
1. 32位浮点数其实只能存储对应表盘上的蓝点值
而不能存储蓝点与蓝点之间的值
2. 蓝点不是均匀分布的, 而是越来越稀疏. 或者说蓝点与蓝点之间的间隔越来越大, 或者说精度越来越低.
这也是为什么到1.xxxxxxx时还能精确到小数点后6位, 到http://1024.xxx时只能精确到小数点后3位, 到8388608 时只能精确到个位数的原因. 因为蓝点越来越稀疏了, 再往后连个位数都精确不到了...
5. 注意事项
I. 区分32位浮点数的存储精度 & 打印效果
在c语言中, 使用 %f 打印时, 默认打印 6 位小数
32位浮点数的有效位数是 7 位有效数
这两者并不冲突, 比如:

原始值 1234.878 89
打印效果 1234.878 906
可见打印效果中只有 前7位 和 原始值 是一致的
事实上, "原始值" vs "打印出来的值" , 其实就是 "你想要存储的值" vs "实际存储的值"
你想要存储1234.878 89, 但实际存储的是1234.878 906... 因为1234.878 906...才是个"蓝点值", 才能真正的被绿色指针所指向, 才能真正的被32位浮点数容器所存储.
虽然不能精确存储你想要保存的值, 但32位浮点数能保证精确存储你想要保存的值的前 7 位. 所以打印效果中的前7位和 原始值 是一致的.
%f 默认打印到6位小数, 打印出来的是实际存储的蓝点值. 但, 蓝点值可不一定是7位小数, 可能有十几位小数, 只是 %f 会默默的将其舍入为7位小数并打印出来
II. 有时候精度不是7位
可能的原因有很多, 比如:
1. 打印时, %f发生了舍入:
此时可以设置打印更多的小数位

2. 好像精确度不止7位
注意, 浮点数中能存储的都其实是蓝点值
所以, 如果 你要存储的值 和 蓝点值 完全一样, 那你要存储的值就能够被完全精确的存储下来的.
如果 你要存储的值 和 蓝点值 非常非常靠近, 就会体现出超乎寻常的精度. 详见下例:

3. 好像精确度不到7位
举例:

对此, 个人理解是:
对于 1024 ~ 2048之间的数, 32位浮点数确实有能力精确到7位有效数
当你要存储的值不是一个蓝点值时, 会发生舍入, 自动舍入到离它最近的一个蓝点值
所以, 1024.001, 会舍入到离它最近的蓝点1024.000976..., 体现的好像精度不足7位
而1024.0011, 就会舍入到离它最近的蓝点1024.00109..., 体现的好像精度又足7位了...
只是说: 32位浮点数确实有精确到7位有效数的能力, 但舍入规则使得它有时好像无法精确到7位...

从这个角度去理解的话, 前面我们讨论过的一个话题就有点站不住脚了:
前面我们说过: :
c语言的float.h中有这样一行代码:
#define FLT_EPSILON 1.192092896e-07F // smallest such that 1.0+FLT_EPSILON != 1.0
↑ 定义常量 FLT_EPSILON, 其值为 1.192092896e-07F
这个 1.192092896e-07F , 其实就是我们1 ~ 2范围中的 间隔: 1.19209e-7
源码中说: 32位浮点数 1.0, 最少也要加上 FLT_EPSILON这个常量, 才能 不等于1.0
换句话说, 如果 1.0 加上一个 小于 FLT_EPSILON 的数 N, 就会出现 1.0 + N == 1.0 这种"诡异的情况".
等等, 这里好像忽略掉了舍入规则: 1 ~ 2范围中, 两个蓝点之间的间隔是: 1.19209e-7, 但这并不意味着想从当前蓝点走到下一个蓝点需要走满一个间隔啊, 因为有舍入规则的存在, 其实你只要走大半个间隔就行了, 然后舍入规则会自动把你舍入到下一个蓝点...

在c语言中验证一下:

测试环境: win10 1909, gcc version 6.3.0 (MinGW.org GCC-6.3.0-1)
可见, 因为有舍入机制的存在, 一个蓝点想移动到下一个蓝点: 大体上只需移动间隔的一半多一点即可.
而c语言中的这行注释:
#define FLT_EPSILON 1.192092896e-07F // smallest such that 1.0+FLT_EPSILON != 1.0
其实也不太对, 1.0 也不需要加上 FLT_EPSILON 这一整个间隔才能 != 1.0 (或者说才能到下一个蓝点), 大体上只需加上 FLT_EPSILON的一半多一点 就能 !=1.0 了(或者说就能到下一个蓝点了).

不过这也只是个人理解...
III. 0.xxxxxxx 到底能精确到小数点后几位
或者说, 32位浮点数能记录7位有效数, 那对于 0.xxxxxxx 这种格式的数, 到底是能精确到小数点后7位, 还是小数点后6位. 或者说, 此时整数部分的0算不算有效数...
个人理解, 对于0.xxxxxxx这也的小数, 其实能精确到小数点后7位, 即0不算一位有效数
以0.5 ~ 1这个范围为例, 此时的间隔是间隔是5.96046e-8, 约等于0.0000 0006
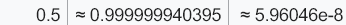
下面尝试精确到小数点后8位, 发现不行.

但精确到小数点后7位确是绰绰有余:

而0 ~ 0.5之间, 间隔则会更小, 精度则会更高 (因为浮点数表盘上的蓝点是越来越稀疏, 精度越来越差的. 如果靠后的0.5 ~ 1范围中能精确到小数点后7位, 那更靠前的0 ~ 0.5中只会更精确, 或者说蓝点只会更密集, 间隔只会更小)
举例:

总之还是那就话: 大体来说, 32位浮点数的精度是7位有效数.
事实上, 浮点数中只能存储蓝点, 蓝点越靠近0就越密集, 精度就越高. ←7位有效数是对这一现象的总结和概括性描述
最后说一点: 有些同学可能会错误的认为32位浮点数类型的精度是: 始终能精确到小数点后6位, 比如能精确存储999999.123456, 但不能精确存储999999.1234567
相信读到这里, 大家都能找出这种理解的错误之处了: 32位浮点数的精确度是7位有效数, 大体来说, 这7位有效数, 指的是 整数 + 小数一共7位, 而不是说始终能精确到小数点后六位...
IV. 深入理解间隔表
我们再回头看看这张wiki上的间隔表. 其实它主要就是在告诉我们: 某个范围中, 两个蓝点间的间隔是多少.
比如在1 ~ 2范围中, 两个蓝点间的间隔约是1.19209e-7
在 8388608 ~ 16777215范围中, 两个蓝点间的间隔是1

这里其实有几个注意事项:
1. 每个范围中, 都有2^32个蓝点, 或者每个区间都被等分为2^23个间隔
比如范围1~2会被等分为2^23个间隔, 范围 8388608 ~ 16777215 也会被等分为2^23个间隔
2. 范围的划分由指数决定
所谓的范围1~2会被等分为2^23个间隔, 准确来说应该是范围2^0 ~ 2^1会被等分为2^23个间隔
所谓的范围8388608 ~ 16777215会被等分为2^23个间隔, 准确来说应该是范围2^23 ~ 2^24会被等分为2^23个间隔
每次指数位变更, 都会划分出新的范围. 这其实很好理解:
比如, 现在我们位于起点: 0 00000010 00000000000000000000000
往前移动2^23 - 1步, 或者说往前移动2^23 - 1个间隔, 对应的其实就是把尾数从00000000000000000000000, 一步步变成11111111111111111111111
再往前走一步, 也就是共往前移动了2^23个间隔, 我们来到了终点: 0 00000011 00000000000000000000000
可见终点相对起点, 仅指数位增长了1
终点到起点, 就确定了一段范围. 该范围被等分成了2^23个间隔. (终点 - 起点) / 2^23就是每个间隔的长度.
再往前走2^23个间隔, 就来到了0 00000100 00000000000000000000000, 同样是指数变大了1...
这就不难看出: 指数位的变更用于划分范围, 尾数位的变更用于往前一步步移动.
有多少个尾数位, 决定了每个范围中可以划分出多少个间隔, 比如有23个尾数位, 就意味着每个范围中可以划分出2^23个间隔
有多少指数位, 决定我们可以囊括多少的范围. 比如有8个指数位 (可表示的指数范围是[-127, 128]), 那我们的范围划分就是这样的:
2^-127 ~ 2^-126是一个范围
2^-126 ~ 2^-125是一个范围
...
2^0 ~ 2^1 是一个范围
2^1 ~ 2^2 是一个范围
...
2^127 ~ 2^128 是一个范围
上面每个范围都会被尾数位等分为2^23份间隔
增大指数位不会增大精度: 比如, 如果将指数位增大到16位(可表示的指数范围是[-32767, 32768]), 那我们的范围划分是这样的
2^-32767 ~ 2^-32766是一个范围
2^-32766 ~ 2^-32765是一个范围
...
2^-127 ~ 2^-126是一个范围
2^-126 ~ 2^-125是一个范围
...
2^0 ~ 2^1 是一个范围
2^1 ~ 2^2 是一个范围
...
2^32767 ~ 2^32768是一个范围
上面每个范围依旧会被尾数位等分为2^23份间隔
注意: 2^0 ~ 2^1, 这个范围还是被等分为2^23份间隔, 2^-126 ~ 2^-125, 这个范围还是被等分为2^23份间隔...
每个范围的精度都没有任何提升.
增大尾数位才会增大精度: 比如, 将尾数位增大为48. 则每个范围会被等分为2^48份间隔. 这样每个范围中的间隔才会变小, 蓝点才会变密集, 精度才会提升.
总结: 指数位的多少控制着能囊括多少个范围, 尾数位的多少控制着每个范围的精度, 或者说控制着每个范围中间隔的大小, 蓝点的密度.
希望这能让你对ieee754标准中的指数位, 尾数位的 具体作用, 控制什么 有更好的理解.
四. 理解角度2: WIKI中的计算方法
理解角度2倒是相当简单.
我们说过, 32位浮点数在内存中是这样表示的: 1位符号位, 8位指数位, 23位尾数位
事实上尾数位是24位, 因为在尾数位前还隐藏了一个整数部分1. 或 0. (可以参见本系列的第一篇文章)
仔细想一下, 浮点数内存的三个部分中:
符号位: 用于控制正负号
指数位: 控制指数, 其实也就是控制小数点的移动:
就好像在十进制中:
1.2345e2 = 123.45
1.2345e3 = 1234.5, 指数位+1只是把小数点向后移动了一位. 二进制中也是一样的, 指数位也仅仅用于控制小数点的移动. 比如0.01 → 0.001 (小数点向左移动了一位)
尾数位: 其实真正控制精度的, 或者说真正记录状态的, 只有尾数位.
在24位尾数中
从: 0.0000 0000 0000 0000 0000 000
到: 0.0000 0000 0000 0000 0000 001
...
一直到: 1.1111 1111 1111 1111 1111 111
共包含2^24种状态, 或者说能精确记录2^24种不同的状态:
0.0000 0000 0000 0000 0000 000 是一种状态,
0.0000 0000 0000 0000 0000 001 又是一种状态,
1.0010 1100 0100 1000 0000 000 又是另一种状态
...
如果你准备记录2^24 + 1种状态, 那尾数就不够用了. 或者说就不能满足你对精度的需求了.
在这种视角下: 精度 和 可表示的状态数 之间画上了等号.
总结一下: 32位浮点数一共能记录2^24种状态 (符号位用于控制正负, 指数位用于控制小数点的位置. 只有尾数位用于精确记录状态)
对于 float f = xxx; 其中xxx是个数值, 不管xxx你是用什么进制书写, 只要是使用32位浮点数作为容器, 就最多只能精确记录2^24种状态, 就好像一个32位浮点数大楼中一共有2^24个房间一样.
事实上, xxx我们一般用10进制书写,
而2^24 = 16 777 216(十进制), 即32位浮点数容器最多只能存储16 777 216(十进制)种状态
16 777 216 是个8位数
所以32位浮点数的精度最多是7位十进制(0 - 9 999 999), 共10 000 000种状态
如果32位浮点数的精度是8位十进制的话(0 - 99 999 999), 这一共是100 000 000种状态, 大于了32位浮点数能存储的状态上限16 777 216...所以说精度到不了8位十进制数.
到这里就分析完毕了.
如果你更喜欢数学表达式的话, 那么 "32位浮点数的精度最多是N位十进制" , N是这样算出来的:

下面是wiki中对该算法的描述:
The number of decimal digits precision is calculated via number_of_mantissa_bits * Log10(2). Thus ~7.2 and ~15.9 for single and double precision respectively.
如wiki中所说, 32位浮点数的精度大约是7位十进制数, 64位浮点数的大约是16位十进制数.
注: 对于这两种理解角度: 理解角度2更简单一些, 可以直接用数学公式计算出精度. 理解角度1(也就是从间隔的角度去理解)的解释性更强一些, 细节更丰富, 能解释的现象也更多一些.
五. 总结
本章大体总结了 "32位浮点数的精度是7位十进制数" 的两种计算方法. 关于这一话题, 网上的资料比较混乱, 所以这里加入了一些自己的理解. 如有错误还望指出.