利用中心差分格式求解一阶波动方程(附Matlab代码)
∂ 2 u ∂ t 2 − ∂ 2 u ∂ x 2 = 0 , 0 < x < 1 , t > 0 , \frac{\partial^2u}{\partial t^2}-\frac{\partial^2u}{\partial x^2}=0,0<x<1,t>0, ∂t2∂2u−∂x2∂2u=0,0<x<1,t>0,
初始边值条件为:
u ( 0 , x ) = 2 s i n ( π x ) , u\left(0,x\right)=2sin\left(\pi x\right), u(0,x)=2sin(πx),
u t ( 0 , x ) = 0 , 0 < x < 1 , u_t\left(0,x\right)=0,0<x<1, ut(0,x)=0,0<x<1,
u ( t , 0 ) = u ( t , 1 ) = 0 , t ≥ 0. u\left(t,0\right)=u\left(t,1\right)=0,t\geq0. u(t,0)=u(t,1)=0,t≥0.
精确解: u = s i n ( π ( x − t ) ) + s i n ( π ( x + t ) ) 。 u=sin\left(\pi\left(x-t\right)\right)+sin\left(\pi\left(x+t\right)\right)。 u=sin(π(x−t))+sin(π(x+t))。
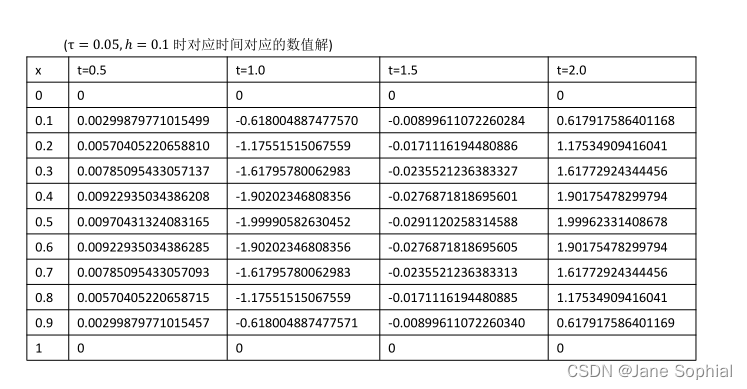
(1) 取 τ \tau τ=0.05,h=0.1计算 t = 0.5,1.0,1.5,2.0 的解。
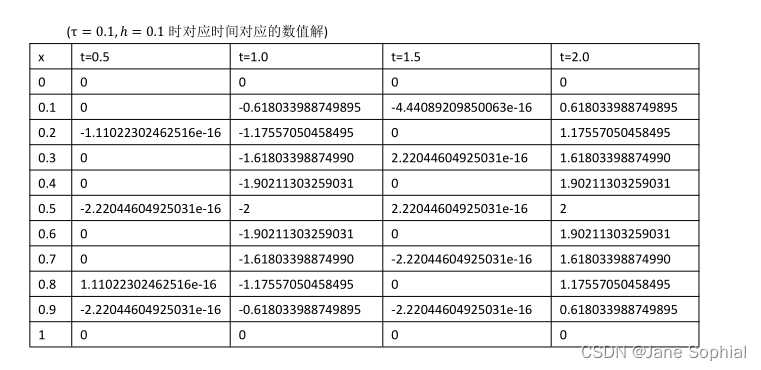
(2) 取 τ \tau τ=h=0.1,计算 t = 0.5,1.0,1.5,2.0 的解。
解:
(1)问题分析
Step 1:网格剖分
取时间步长 τ = T N \tau=\frac{T}{N} τ=NT和空间步长 h = l J h=\frac{l}{J} h=Jl,记矩形区域 G = 0 ≤ t ≤ T , 0 ≤ x ≤ l G = {0 \le t \le T, 0 \le x \le l} G=0≤t≤T,0≤x≤l。用两族平行直线把这个区域 G 分割成矩形网格。网格节点用坐标点来 ( t n , x j ) \left(t_n,x_j\right) (tn,xj)表示。 G h G_h Gh表示网格内点的集合。 Γ h = G / G h = G − G h \Gamma_h=G/G_h=G-G_h Γh=G/Gh=G−Gh表示界点的集合。用 u ( t n , x j ) u\left(t_n,x_j\right) u(tn,xj)表示真解, u j n u_j^n ujn表示在 ( t n , x j ) \left(t_n,x_j\right) (tn,xj)处的近似值。定义网比 r 2 = τ 2 h 2 r^2=\frac{\tau^2}{h^2} r2=h2τ2。
Step 2:差分方程,中心差分格式
u j n + 1 − 2 u j n + u j n − 1 = r 2 ( u j + 1 n − 2 u j n + u j − 1 n ) u_j^{n+1}-2u_j^n+u_j^{n-1}=r^2\left(u_{j+1}^n-2u_j^n+u_{j-1}^n\right) ujn+1−2ujn+ujn−1=r2(uj+1n−2ujn+uj−1n)
⇒ u j n + 1 = r 2 ( u j − 1 n + u j + 1 n ) + 2 ( 1 − r 2 ) u j n − u j n − 1 ( 1 ) \Rightarrow u_j^{n+1}=r^2\left(u_{j-1}^n+u_{j+1}^n\right)+2\left(1-r^2\right)u_j^n-u_j^{n-1} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1) ⇒ujn+1=r2(uj−1n+uj+1n)+2(1−r2)ujn−ujn−1 (1)
由初值条件得: u j 0 = s i n ( π x j ) , u j 1 − u j − 1 2 τ = 0. u_j^0=sin\left(\pi x_j\right),\frac{u_j^1-u_j^{-1}}{2\tau}=0. uj0=sin(πxj),2τuj1−uj−1=0.
(1)式中令n=0, 得: u j 1 = r 2 ( u j − 1 0 + u j + 1 0 ) + 2 ( 1 − r 2 ) u j 0 − u j − 1 ,消去 u j − 1 u_j^1=r^2\left(u_{j-1}^0+u_{j+1}^0\right)+2\left(1-r^2\right)u_j^0-u_j^{-1},消去u_j^{-1} uj1=r2(uj−10+uj+10)+2(1−r2)uj0−uj−1,消去uj−1,得:
u j 1 = r 2 ( s i n ( π x j − 1 ) + s i n ( π x j + 1 ) ) + ( 1 − r 2 ) s i n ( π x j ) . u_j^1=r^2\left(sin\left(\pi x_{j-1}\right)+sin\left(\pi x_{j+1}\right)\right)+\left(1-r^2\right)sin\left(\pi x_j\right). uj1=r2(sin(πxj−1)+sin(πxj+1))+(1−r2)sin(πxj).
令 U n = ( u 1 n , u 2 n , ⋯ , u J − 1 n ) T , {\ U}^n=\left(u_1^n,u_2^n,\cdots,u_{J-1}^n\right)^T, Un=(u1n,u2n,⋯,uJ−1n)T, A = [ 2 ( 1 − r 2 ) r 2 0 ⋯ 0 0 0 r 2 2 ( 1 − r 2 ) r 2 ⋯ 0 0 0 ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ 0 0 0 0 ⋯ r 2 2 ( 1 − r 2 ) r 2 0 0 0 ⋯ 0 r 2 2 ( 1 − r 2 ) ] A=\left[\begin{matrix}2\left(1-r^2\right)&r^2&0&\cdots&0&0&0\\r^2&2\left(1-r^2\right)&r^2&\cdots&0&0&0\\\cdots&\cdots&\cdots&\cdots&\cdots&\cdots&0\\0&0&0&\cdots&r^2&2\left(1-r^2\right)&r^2\\0&0&0&\cdots&0&r^2&2\left(1-r^2\right)\\\end{matrix}\right] A=
2(1−r2)r2⋯00r22(1−r2)⋯000r2⋯00⋯⋯⋯⋯⋯00⋯r2000⋯2(1−r2)r2000r22(1−r2)
为一个 J − 1 × J − 1 J-1×J-1 J−1×J−1,的单位矩阵,特别地, U 0 = ( 2 s i n ( π x 1 ) , 2 s i n ( π x 2 ) , ⋯ , 2 s i n ( π x J − 1 ) ) T , U 1 = ( u 1 1 , u 2 1 , ⋯ , u J − 1 1 ) T . {\ U}^0=\left(2sin\left(\pi x_1\right),2sin\left(\pi x_2\right),\cdots,2sin\left(\pi x_{J-1}\right)\right)^T,{\ U}^1=\left(u_1^1,u_2^1,\cdots,u_{J-1}^1\right)^T. U0=(2sin(πx1),2sin(πx2),⋯,2sin(πxJ−1))T, U1=(u11,u21,⋯,uJ−11)T.
(2)上机程序
function [U1,E]=shuangqv(J,N)
x0=0;xJ=1;h=(xJ-x0)/J;x=[x0:h:xJ]';
t0=0;tN=2;tau=(tN-t0)/N;t=[t0:tau:tN]';
r=tau^2/h^2;
u(:,1)=2*sin(pi*x(2:J,1));
for j=1:J-1
u(j,2)=r*(sin(pi*x(j))+sin(pi*x(j+2)))+(1-r)*2*sin(pi*x(j+1));
end
U(:,1)=[u(:,2);u(:,1)];
A=diag(ones(1,J-1))*(2-2*r)+(diag(ones(1,J-2),1)+diag(ones(1,J-2),-1))*r;
E=diag(ones(1,J-1));
B=[A,-E;E,zeros(J-1,J-1)];
for n=2:N+1
U(:,n)=B*U(:,n-1);
end
U1=U(J:2*(J-1),:);
U1=[zeros(1,N+1);U1;zeros(1,N+1)];
for j=1:J+1
for n=1:N+1
V(j,n)=sin(pi*(x(j)-t(n)))+sin(pi*(x(j)+t(n)));
end
end
E=max(max(abs(U1-V)));
end
%调试
clear all;clc;close all;
[U1,E1]=shuangqv(10,40);
[U2,E2]=shuangqv(10,20);
(3)问题结果
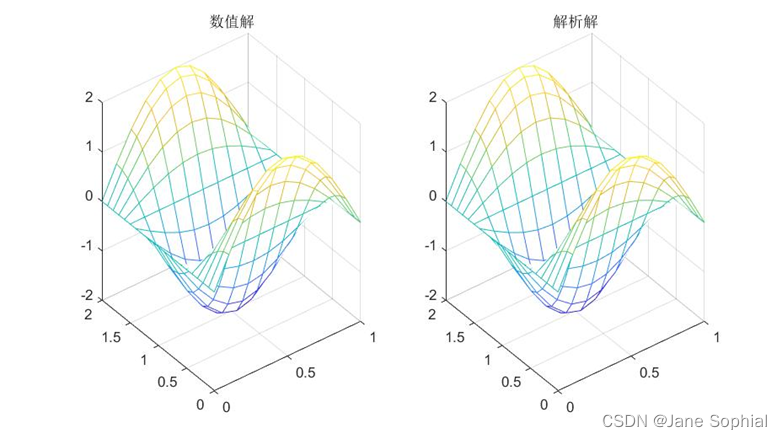 ( τ \tau τ=h=0.1时,解析解与数值解图像)
( τ \tau τ=h=0.1时,解析解与数值解图像)
由图像可以看出,解析解与数值解的图像高度吻合。接着我们看一下两种情况下的最大误差:
| 最大误差 | |
|---|---|
| τ \tau τ=0.05,h=0.1 | 0.029747384249724 |
| τ \tau τ=0.1,h=0.1 | 1.665334536937735e-15 |
( τ \tau τ=0.05,h=0.1时对应时间对应的数值解)
( τ \tau τ=0.1,h=0.1时对应时间对应的数值解)