一文讲透时间序列的平稳性

本文转载自知乎作者StormBlafe，编辑：时序人

原文链接：http://zhuanlan.zhihu.com/p/652229829

1►

为什么要关注时间序列的平稳性？

原因一：时间序列数据的数据结构与传统的统计数据结构不同。最大的区别在于，传统随机变量可以得到多个观测值（比如骰子点数，可以反复掷得到多个观测值，忽略时间的差异）。而时间序列数据中，每个随机变量只有一个观测值（比如设收盘价为研究的随机变量，每天只有一个收盘价，不同日子的价格服从的分布不同，即考虑时间的差异）。这样一来，每个分布只能得到一个观测值，数目太少，无法研究分布的性质。但是通过平稳性，从不同日期的分布之间发现内在关联，缓解了由于样本容量少导致的估计精度低的问题。

原因二：研究时间序列的最终目的是，预测未来。但是未来是不可知的，我们拥有的数据都是历史，因此只能用历史数据来预测未来。但是，如果过去的数据与未来的数据没有某种“相似度”，那这种预测就毫无道理了。平稳性就是保证这种过去与未来的相似性，如果数据是平稳的，那么可以认为过去的数据表现出的某些性质，未来也会表现。

因此，当未来的数据与现在相似时，它更容易建模。平稳性描述了时间序列的统计特征不随时间变化的概念。因此一些时间序列预测模型，如自回归模型，依赖于时间序列的平稳性。一些时间序列预测模型(例如，自回归模型)需要平稳的时间序列，因为它们更容易建模，因为它们具有恒定的统计属性。因此如果时间序列不是平稳的，就应该尽量让它平稳。

2►

什么是严平稳？

对于一个时间序列{Xt}，其中每个数据X都是随机变量，都有其的分布（如图）。

取其中连续的m个数据，X1到Xm，则可以构成一个m维的随机向量，(X1,X2,...,Xm)

由于单独的每个随机变量X都有各自的分布，那么组合成一个m维随机向量后，这个多维向量整体就有一个“联合分布”。

严平稳的本质就是，这种联合分布不随着时间的推移而变化。

也就是说，取数据时，任意连续取出的m个数据（无论是从X1取到Xm，还是从Xt取到Xt+m），他们组成的多维向量的联合分布都是相同的。

此时，再放宽一个条件，让这个m的取值也任意。

即无论这取数据的窗口设定为多宽，只要连续取相同数目个数据，他们构成的联合分布都是相同的。

比如，(X1,X2,X3)与（X6,X7,X8）有相同的3维联合分布，(X1,X2,X3,X4)与（X6,X7,X8,X9）有相同的4维联合分布。

综上，符合上述性质的时间序列，是严平稳的。

3►

有了严平稳，为什么还要有宽平稳？

很多情况下，我们无从得知这些随机变量的分布到底是什么样子。

我们观测得到的数据，只是服从某种未知分布的随机变量的一种取值。

既然连单个随机变量的分布都难以求出，就更不用说求由一堆随机变量组成、多维随机向量的联合分布有多困难了。

因此严平稳虽然是一种保证过去与未来的数据“相似”很棒的方式，但过于理想化，实际上很难检验一个时间序列的严平稳性。

于是只能放宽条件，因而产生了“宽平稳”的概念。

4►

什么是“k阶矩”

“矩”是随机分布的一种特征数。特征数，顾名思义，反映了一个随机分布的某种特征。比如“数学期望”反映了，符合某种分布的随机变量的取值，总是在某个值周围波动；而“方差”则反映了，这种波动的大小程度。

矩分为原点矩和中心矩，其中一阶原点矩就是数学期望，二阶中心矩就是方差。

通常2阶以内（含2阶）称为低阶矩，2阶以上称为高阶矩。

但是这两者之间有相互推导的公式，知其一就可推其二，因此一般只称“矩”。

其中，随机变量的k阶原点矩的定义为，随机变量的k次方的数学期望，即E(Xk)。平时所说的“k阶矩存在”，就表现为这个数学期望不是无穷（也就是小于无穷），这与“极限存在”的定义是同理的。

值得注意的是，如果一个随机变量的某高阶矩存在，那么低阶矩也一定存在。因为|X|k-1≤|X|k+1。

严平稳中由于联合分布相同，故各阶矩也相同。

5►

什么是宽平稳？

宽平稳性是使用序列的特征统计量来定义的，它认为序列的统计性质，主要由其低阶矩决定。

当时间序列满足以下三个条件时：

第一个条件，任意时刻二阶矩都存在。

第二个条件，随机变量的期望（一阶矩）不随时间的推移而改变。说白了就是，均值μ不随时间t改变。

第三个条件，两个时点的随机变量之间的自相关系数，只与这两个时点的时间差有关，而不随时间的推移而改变。说白了就是，只要窗口宽度（即两时点的时间差）固定，则自相关系数是唯一。

就被称为是宽平稳的。

由于定义涉及到的几个条件，宽平稳也被称为协方差平稳，或二阶平稳。

6►

平稳性的一些结论

如果一个时间序列平稳，则有：

均值是与t无关的常数。即不同时点的分布中，随机变量都是围绕同一个值波动的。表现在时序图（横轴为时间轴，纵轴衡量随机变量取值）中，即图线整体是围绕某个水平线波动的（类似于政经里价格围绕价值上下波动那个图）。

方差是与t无关的常数。这在定义里并没有显然地体现，但是由于定义给出自相关系数只与窗口宽度有关，而与窗口位置即时间t无关，所以大可以干脆取个宽度为0的窗口，于是本来相隔一个窗口宽度的两个时点数据之间的相关性，就变成了同一个时点数据自己和自己之间的相关性，自己和自己，当然相关系数为1。

协方差是常数。

严平稳与宽平稳之间的关系？

严平稳本质上是对时间序列的分布进行限制，而宽平稳的本质是对低阶矩进行限制。

由于宽平稳比严平稳的条件更为宽松，因此通常情况下，严平稳能推导出宽平稳，但宽平稳不能反推严平稳。但有特例。

因为宽平稳时，需要满足二阶矩存在的条件。而严平稳不需要满足二阶矩存在。

因此，不存在二阶矩的严平稳序列，无法满足宽平稳。例如严平稳的柯西分布序列，就不符合宽平稳（一二阶矩不存在，因此无法验证宽平稳）。

所以，只有二阶矩存在时，严平稳序列才满足宽平稳。

特例：当序列服从多元正态分布时，宽平稳序列一定能推导出严平稳。

原因在于，正态时间序列的二阶矩平稳，等价于分布平稳（其密度函数表明，n维正态分布仅由其均值向量和自协方差矩阵决定）。

正态时间序列

如果一个时间序列，从中取出任意n个（有限个）随机变量，组成的n维随机向量，都服从n维正态分布，则称之为正态时间序列。即上方的特例。

7►

如何检验平稳性？

你可以用两种方法来测试时间序列的平稳性:

直观的方法：肉眼评估
统计方法：单位根检验

我们将创建几个示例，使用Hyndman 和 Athanasopoulos的时间序列分析教材《Forecasting: principles and practice》中提到方法解释平稳性的视觉评估，并扩展它们的用法，并解释使用单位根测试进行的平稳性测试。数据来自R的fma 包。

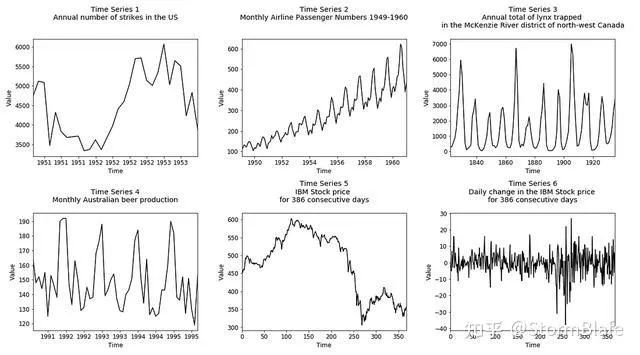
方法一：直观地评估平稳性

最简单的方法是将时间序列分成两半，并比较时间序列的前半部分到后半部分的平均值、振幅和周期长度。

均值常数-时间序列前半段的均值应该与后半段的均值相似。
方差常数-时间序列的前半段的振幅应该与后半段相似。
协方差与时间无关——时间序列前半部分的周期长度应该与后半部分的周期长度相似。周期应该在时间上是独立的(例如，不是每周或每月等)。

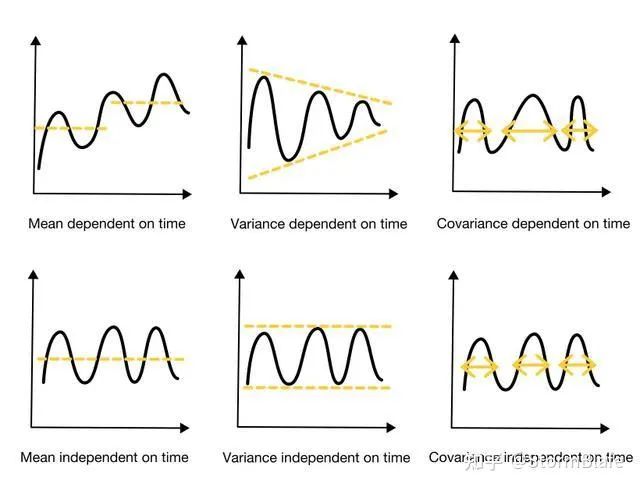
对于我们的例子，评估结果如下图所示：

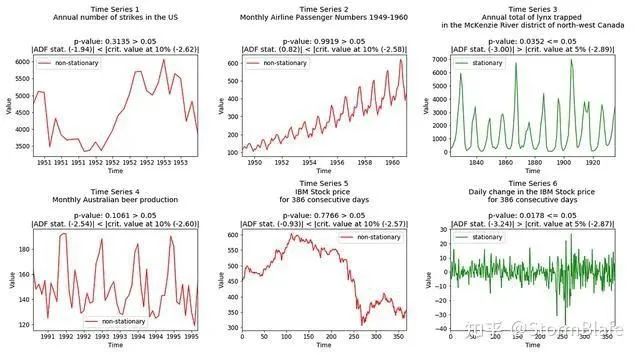
方法二：统计评估平稳性——单位根检验

单位根是一种随机趋势，称为“带漂移的随机游走”。由于随机性无法预测，这意味着:

单位根存在：不稳定（不可预测），单位根不存在：平稳的

为了用单位根检验平稳性，可以将两个这两个假设作为初始假设：

零假设（H0)）- 时间序列是平稳的（没有单位根存在）
备择假设（H1） - 时间序列不是平稳的（存在单位根）

然后根据以下两种方法评估是否拒绝零假设:

p 值方法：

如果 p 值 > 0.05，则无法拒绝原假设。如果 p 值 ≤ 0.05，则拒绝零假设。

临界值法：

如果检验统计量没有临界值那么极端，则无法拒绝原假设。如果检验统计量比临界值更极端，则拒绝原假设。当 p 值接近0.05时，应使用临界值法。

有几个单位根测试可以用来检查平稳性。本文将重点介绍最流行的2个:

Augmented Dickey-Fuller test 和 Kwiatkowski-Phillips-Schmidt-Shin test

方法三：Augmented Dickey-Fuller test

Augmented Dickey-Fuller test的假设为：

H0：时间序列不是平稳的，因为有一个单位根（如果p值> 0.05）

H1：时间序列是平稳的，因为没有单位根（如果p值≤0.05）

在Python中，我们可以直接使用statsmodels.tsa.stattools库中的adfuller方法。

from statsmodels.tsa.stattools import adfuller
result = adfuller(df["example"].values)

如果我们可以拒绝ADF检验的零假设，则时间序列是平稳的：

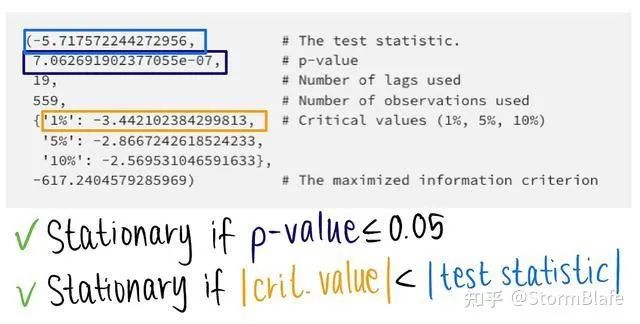
下面是样本数据集的ADF测试结果：

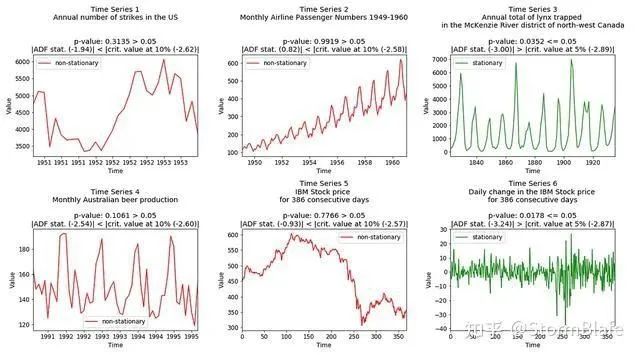
方法四：Kwiatkowski-Phillips-Schmidt-Shin test

Kwiatkowski-Phillips-Schmidt-Shin (KPSS)检验的假设是[4]：

H0：时间序列是平稳的，因为没有单位根（如果p值> 0.05）

H1：时间序列不是平稳的，因为有一个单位根（如果p值≤0.05）

statsmodels.tsa.stattools库中的kpss方法，我们需要使用参数regression = 'ct'来指定检验的零假设是数据是趋势平稳的。

from statsmodels.tsa.stattools import kpss

result = kpss(df["example"].values,
regression = "ct")

如果我们不能拒绝KPSS检验的零假设，则时间序列是平稳的：

下面是样本数据集的KPSS测试结果：

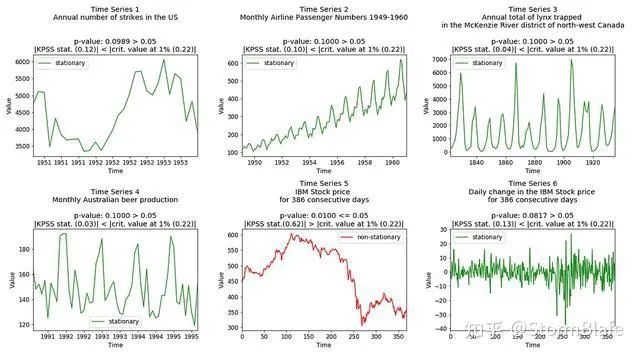
8►

非平稳时间序列数据处理

我们可以对一个非平稳时间序列应用不同的变换，使其接近平稳：因为有几种平稳性类型，所以我们可以结合ADF和KPSS测试来确定要进行哪些变换：

如果ADF测试结果是平稳的，而KPSS测试结果是非平稳的，则时间序列是差分平稳的-对时间序列应用差分，并再次检查平稳。如果ADF检验结果是非平稳性的，而KPSS检验结果是平稳性的，则该时间序列为趋势平稳的-需要去掉去趋势，并再次检查平稳性。

差分

差分计算两个连续观测值之间的差值。它稳定了时间序列的平均值，从而降低了趋势df["example_diff"] = df["example"].diff()

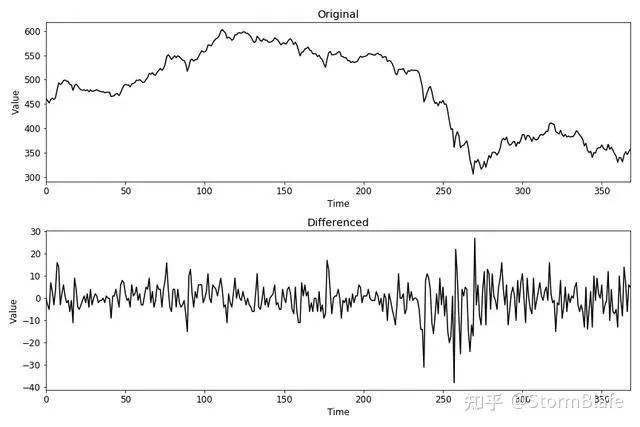
通过模型拟合去趋势

从非平稳时间序列中去除趋势的一种方法是将一个简单的模型(例如，线性回归)拟合到数据上，然后对该拟合的残差进行建模。

from sklearn.linear_model import LinearRegression


# Fit model (e.g., linear model)
X = [i for i in range(0, len(airpass_df))]
X = numpy.reshape(X, (len(X), 1))
y = df["example"].values
model = LinearRegression()
model.fit(X, y)


# Calculate trend
trend = model.predict(X)


# Detrend
df["example_detrend"] = df["example"].values - trend

结果如下：

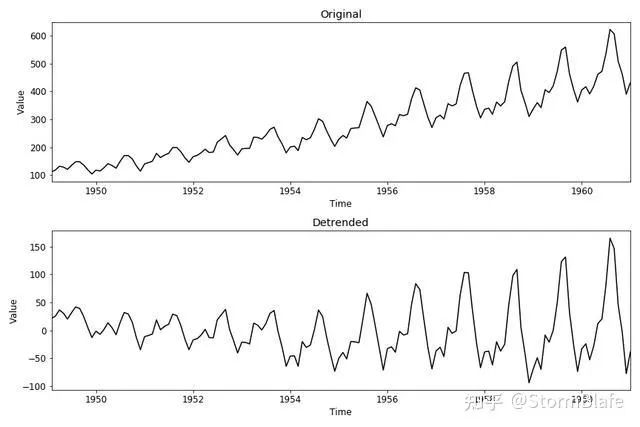
可见，去趋势并没有直接将序列从非平稳转变为平稳，但是离平稳更近了一步。

对数变换

对数变换可以稳定时间序列的方差。

df["example_diff"] = np.log(df["example"].value)

结果如下：

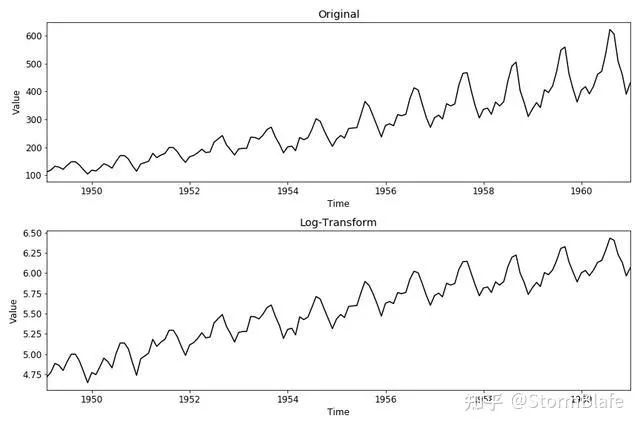
正如你所看到的，模型拟合的去趋势和对数变换都不能使我们的例子时间序列平稳。所以需要结合不同的技术使时间序列平稳。例如通过对数转换来改善方差常数，再通过去趋势来改善均值常数项，最终达到数列的平稳。

9►

几种常见的、特殊的平稳与非平稳序列

平稳时间序列

白噪声

一种最简单的平稳时间序列就是白噪声——具有零均值同方差的独立同分布序列，记作。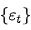

当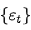服从均值为0的正态分布时，称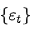为高斯白噪声或正态白噪声。

对于任意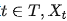均值相同、方差相同，独立则协方差为0，故而白噪声序列是平稳的。

当一个序列为白噪声时，表示序列前后没有任何相关关系。过去的行为对将来的发展没有丝毫影响，从统计分析的角度而言，已没有任何分析建模的价值。未来的趋势亦无法预测，因为白噪声的取值是完全随机的。

此时未来预测为均值就是残差最小的选择。

只有当序列平稳且非白噪声时，应用ARMA等分析方法才有意义。

通常我们在对时间序列建模之后，还会对残差序列进行白噪声检验，如果残差序列是白噪声，那么就说明原序列中所有有价值的信息已经被模型所提取；如果非白噪声就要检查模型的合理性了。

简单用一行代码就能生成白噪声序列。

非白噪声

平稳时间序列可不止白噪声，生活中也会有平稳的时间序列，但却是很少。也别灰心，很多序列是可以经过简单处理后变为平稳的非白噪声序列。数据整体均值、方差直观上看也没有大的变化，大体上可以认为是平稳的。你要说这样判断太武断，确实还可以通过统计量化的方式检验序列是否平稳，如ADF检验、KPSS检验等。

我国06年以来的季度GDP数据季节差分后，就可以认为是一个平稳的时间序列。

import numpy as np
import pandas as pd
import akshare as ak
from matplotlib import pyplot as plt

df = ak.macro_china_gdp()
df = df.set_index('季度')
df.index = pd.to_datetime(df.index)

gdp = df['国内生产总值-绝对值'][::-1].astype('float')

gdp_diff = gdp.diff(4)

plt.figure(figsize=(12, 6))
gdp_diff.plot()
plt.show()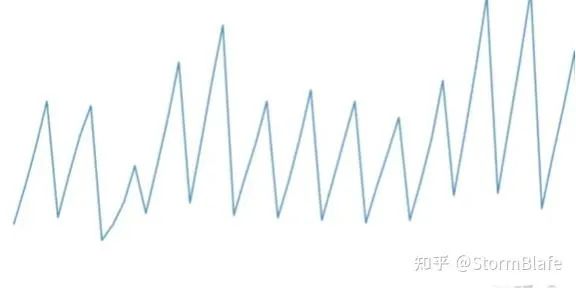

非平稳时间序列

大多数时间序列都是非平稳的，一般可以通过差分、取对数等方法转化成平稳时间序列，若不成就不能使用平稳时间序列分析方法了。虽说还有各种非平稳时间序列的分析方法，预测好坏看各家本领，但终归不如平稳时间序列分析来的省心。

比如一些股票的收盘价数据就是非平稳的。下图是2019～2021年来伊份的每日收盘价数据，整体看上去走势无明显规律，且不同时段波动不一，就可以认为是一个非平稳的时间序列。若平稳且不是白噪声多好啊。

import pandas as pd
import akshare as ak
from matplotlib import pyplot as plt

df = ak.stock_zh_a_hist(symbol="603777", start_date="20190101", end_date='20210616')
df = df.set_index('日期')
df.index = pd.to_datetime(df.index)

close = df['收盘'].astype(float)
close = close[::-1]

plt.figure(figsize=(12, 6))
plt.plot(close)
plt.show()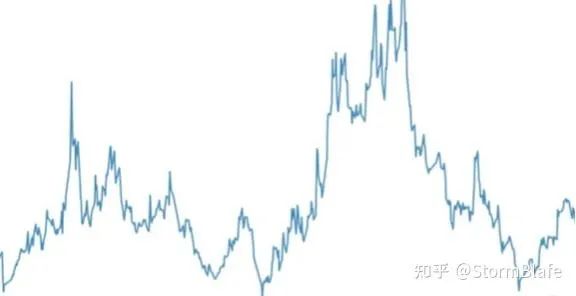

随机游走

有一类特殊的非平稳时间序列叫随机游走，很简单，也很有意思。

一个简单随机游走过程定义为：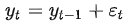

其中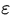是均值为零的白噪声。

用两行代码来模拟一下随机游走过程：

import numpy as np
from matplotlib import pyplot as plt

y = np.random.standard_normal(size=1000)
y = np.cumsum(y)

plt.figure(figsize=(12, 6))
plt.plot(y)
plt.show()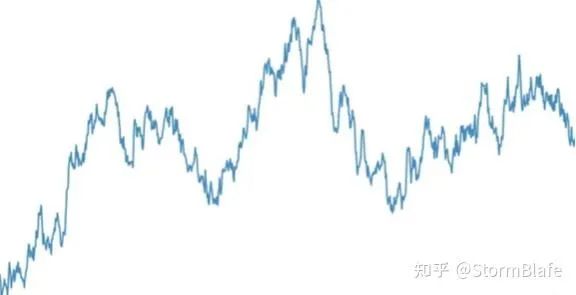

金融领域中有个概念叫有效市场假说，就认为股票的价格是随机游走的，也就是说我们刚刚举的那个上证指数的例子就是随机游走的。以上随机游走的示例图和之前的股价数据走势图比较一下，是不是有点那么个意思。

一个随机游走过程对过去发生的信息具有完美的记忆，如醉汉走路，每一步都是在上一步的位置上胡乱的走，故而能够积累起点以来的每一步信息。初起离家，偶有归时，不知所终。均值为零，方差无限大。

import numpy as np
from matplotlib import pyplot as plt

np.random.seed(5)

def random_walk():
    steps = np.random.standard_normal(size=1000)
    steps[0] = 0
    walk = np.cumsum(steps)
    return walk
    
plt.figure(figsize=(12, 6))
plt.plot(random_walk())
plt.plot(random_walk())
plt.show()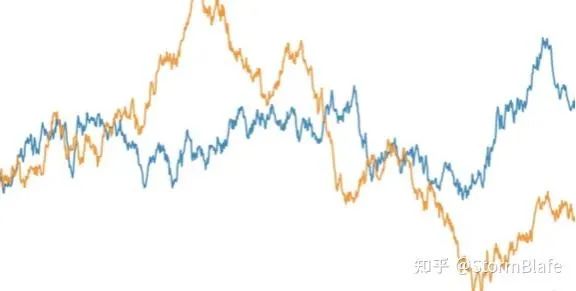

生活中还有一个现象和随机游走有关，叫“久赌必输”。每次赌博时输赢总是不确定的（假设胜率50%，胜负五五开），每次赌博的输赢作为一个随机变量，可以认为是步长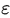，手里的钱数会随着每次输赢而变化，故而赌博时手中的钱服从随机游走模型。手中累积的钱数走势就像上图中的曲线，但却不会一直延展下去。当曲线触碰到下届时（手中的钱输光时），游戏也就结束了；或当曲线触碰到上界时（庄家的钱没有了，贪心到赢钱停不下来要一直赢下去），游戏同样也会结束。庄家的钱无限多，则必然是赌徒输光。庄家的钱再少，也比赌徒的本金多的多。所以上界不知在哪，下界却很清晰，曲线游走到上界的概率几乎为零，输光的终归是赌徒，更别提胜率往往不足50%。

带漂移项的随机游走

带漂移项的随机游走，就是随机游走中加入一个常数，如此而已。

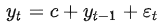
其中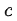是常数，称作位移项或漂移项。

漂移项使得随机游走序列产生了长期趋势。长期趋势的斜率对应漂移项，漂移项为正则有增长趋势，漂移项为负则有下降趋势。

同样代码模拟一下下：

import numpy as np
from matplotlib import pyplot as plt

np.random.seed(123)

y = np.random.standard_normal(size=100)
y1 = np.cumsum(0.2+y)
y2 = np.cumsum(-0.2+y)

l1 = np.cumsum(0.2 * np.ones(len(y1)))
l2 = np.cumsum(-0.2 * np.ones(len(y2)))

plt.figure(figsize=(12, 6))
plt.plot(y1)
plt.plot(y2)
plt.plot(l1)
plt.plot(l2)
plt.show()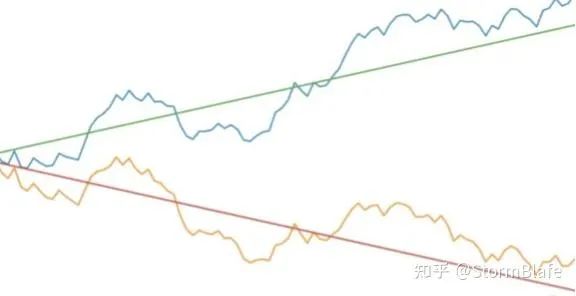

无论是简单随机游走，还是带漂移项的随机游走，都可以通过差分的方式转换为纯随机的平稳时间序列--白噪声。

随机游走的一阶差分即为白噪声：

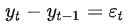
带漂移项的随机游走一阶差分为白噪声+常数：

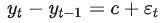
10►

总结

在时间序列预测中，具有恒定统计属性(均值、方差和协方差)且与时间无关的时间序列被描述为平稳的。由于稳定的统计特征，平稳时间序列比非平稳时间序列更容易建模。所以很多时间序列预测模型都假设了平稳性。

平稳性可以通过目测或统计方法进行检查。统计方法检查单位根，最流行的两种单位根测试是ADF和KPSS。这两种工具都可以在Python stattools库中找到。

如果时间序列是非平稳的，可以尝试通过差分、对数转换或去除趋势来使其接近平稳。