写在前面
1、本文内容
使用Eigen进行最小二乘拟合曲线
2、平台/环境
Eigen(open3d), cmake, pcl
3、转载请注明出处:
https://blog.csdn.net/qq_41102371/article/details/131407456
曲线拟合方法
pcl实现的b样条曲线拟合
参考:
https://blog.csdn.net/qq_36686437/article/details/114160557
从效果上看,pcl里面的曲线拟合得到的结果比较差
最小二乘曲线拟合
原理
在二维XOY平面上,曲线由多项式 f ( x ) f(x) f(x)表示:
f ( x ) = a 0 + a 1 x + a 2 x 2 + a 3 x 3 + . . . + a n x n = ∑ i = 0 n a i x i f(x) = a_0+a_1x+a_2x^2+a_3x^3+...+a_nx^n=\sum_{i=0}^n{a_ix^i} f(x)=a0+a1x+a2x2+a3x3+...+anxn=i=0∑naixi
其中 i ∈ { 0 , 1 , 2... n } i\in\{0,1,2...n\} i∈{
0,1,2...n}是多项式的阶数, a i a_i ai是多项式的各阶系数
有一真实曲线 l l l,由m个点组成 ( x j , y j ) , j ∈ { 0 , 1 , . . . m } (x_j,y_j),j\in\{0,1,...m\} (xj,yj),j∈{
0,1,...m},假设 l l l就是由一条确定的多项式曲线 f ( x ) f(x) f(x)采样得到,那么点都在一定曲线上:
y j = f ( x j ) y_j = f(x_j) yj=f(xj)
但实际上,我们是想通过一条拟合出来的曲线 f ( x ) f(x) f(x)来逼近真实点 y j y_j yj以满足每个真实点都在曲线上或者离曲线很近,设每个点离曲线的距离为:
e j = y j − f ( x j ) e_j = y_j-f(x_j) ej=yj−f(xj)
那么我们希望所有真实点离曲线 f ( x ) f(x) f(x)越近越好,则需要最小化所有点到曲线的距离:
m i n x ∑ j = 0 j = m y j − f ( x j ) \mathop{min}\limits_{x}\ \sum_{j=0}^{j=m}{y_j-f(x_j)} xmin j=0∑j=myj−f(xj)
假设我们以一个二阶多项式 f ( x ) = a 0 + a 1 x 1 + a 2 x 2 f(x) = a_0+a_1x^1+a_2x^2 f(x)=a0+a1x1+a2x2拟合数据 ( x j , y j ) , j ∈ { 0 , 1 , . . . m } (x_j,y_j),j\in\{0,1,...m\} (xj,yj),j∈{
0,1,...m},则有方程组:
{ a 0 + a 1 x 0 + a 2 x 0 2 = y 0 a 0 + a 1 x 1 + a 2 x 1 2 = y 1 . . . a 0 + a j x 1 + a 2 x j 2 = y j . . . a 0 + a 1 x m + a 2 x m 2 = y m \begin{cases} a_0 + a_1x_0+a_2x_0^2=y_0 \\ a_0 + a_1x_1+a_2x_1^2=y_1 \\ ...\\ a_0 + a_jx_1+a_2x_j^2=y_j \\ ...\\ a_0 + a_1x_m+a_2x_m^2=y_m \end{cases} ⎩
⎨
⎧a0+a1x0+a2x02=y0a0+a1x1+a2x12=y1...a0+ajx1+a2xj2=yj...a0+a1xm+a2xm2=ym
写成矩阵形式则为
[ 1 x 0 x 0 2 1 x 1 x 1 2 . . . 1 x m x m 2 ] [ a 0 a 1 a 2 ] = [ y 0 y 1 . . . y m ] \begin{bmatrix} 1 & x_0& x_0^2 \\ 1 & x_1& x_1^2 \\ ... \\ 1 & x_m& x_m^2 \\ \end{bmatrix} \begin{bmatrix} a_0\\a_1\\a_2\\ \end{bmatrix}= \begin{bmatrix} y_0\\y_1\\...\\y_m \end{bmatrix}
11...1x0x1xmx02x12xm2
a0a1a2
=
y0y1...ym
这其实是一个非齐次线性方程组 A x = b Ax = b Ax=b的最小二乘解问题,为了不和上面的a和x引起歧义,我们使用 X θ = b X\theta=b Xθ=b表示,其最小二乘问题表示为:
m i n θ ∣ ∣ X θ − b ∣ ∣ 2 \mathop{min}\limits_{\theta}||X\theta-b||^2 θmin∣∣Xθ−b∣∣2
b b b就是 y j y_j yj, X X X就是我们的数据:
[ 1 x 0 x 0 2 1 x 1 x 1 2 . . . 1 x m x m 2 ] \begin{bmatrix} 1 & x_0& x_0^2 \\ 1 & x_1& x_1^2 \\ ... \\ 1 & x_m& x_m^2 \\ \end{bmatrix}
11...1x0x1xmx02x12xm2
我们要求的就是系数 [ a 0 , a 1 , a 2 ] T [a_0,a_1,a_2]^T [a0,a1,a2]T即 X θ = b X\theta=b Xθ=b里面的 θ \theta θ
对于 X θ = b X\theta=b Xθ=b的解,可以做如下变换:
X T X θ = X T b X^TX\theta=X^Tb XTXθ=XTb
我们假设 X T X X^TX XTX可逆,则有:
θ = ( X T X ) − 1 X T b \theta=(X^TX)^{-1}X^Tb θ=(XTX)−1XTb
这里有个问题
1、对于通用最小二乘来说, X T X X^TX XTX可能不可逆,因为 X X X的行向量可能线性相关(详解岭回归与L2正则化),但是在这里,我们注意到每行都有齐次项1,所以当 x 0 ≠ x 1 ≠ . . . ≠ x m x_0 \ne x_1 \ne ...\ne x_m x0=x1=...=xm时, X X X的行向量线性无关,即当数据中无重复点时,我们认为 X T X X^TX XTX可逆,于是通过 θ = ( X T X ) − 1 X T b \theta=(X^TX)^{-1}X^Tb θ=(XTX)−1XTb,我们便可以通过解析解直接得到我们想要的 θ \theta θ
2、我们也可以认为 X T X X^TX XTX不可逆那么 θ = ( X T X ) − 1 X T b \theta=(X^TX)^{-1}X^Tb θ=(XTX)−1XTb的推导可以参考,并且计算时使用Qr分解:
基于最小二乘法的多项式曲线拟合:从原理到c++实现
最小二乘问题和基于HouseHolder变换的QR分解
一文让你彻底搞懂最小二乘法(超详细推导)
代码
提供两种求解的代码,一种是直接通过 θ = ( X T X ) − 1 X T b \theta=(X^TX)^{-1}X^Tb θ=(XTX)−1XTb并利用Eigen的矩阵运算实现,另一种是qr分解。代码目录结构如下,请将least_square_fit_curve.cpp和CMakeLists.txt放入src,然后使用compile.bat和run.bat进行编译和运行,请修改对应PCL对应的路径
least_square_fit_curve.cpp
#include <iostream>
#include <string>
#include <vector>
#include <random>
#include <pcl/visualization/pcl_visualizer.h>
#include <pcl/visualization/pcl_plotter.h>
#include <pcl/point_types.h>
#include <pcl/io/pcd_io.h>
#include <vtkPolyLine.h>
#include <Eigen/Dense>
#include <Eigen/Core>
std::vector<Eigen::Vector2d> GenerateGaussNoise(const std::vector<Eigen::Vector2d> &points_origin, double mu, double sigma)
{
std::vector<Eigen::Vector2d> points_noise;
points_noise = points_origin;
std::normal_distribution<> norm{
mu, sigma};
std::random_device rd;
std::default_random_engine rng{
rd()};
for (size_t i = 0; i < points_noise.size(); ++i)
{
points_noise[i][0] = points_noise[i][0] + norm(rng);
points_noise[i][1] = points_noise[i][1] + norm(rng);
}
return points_noise;
}
void DisplayLine2D(std::vector<double> vector_1, std::vector<double> vector_2, std::vector<double> coeff, double min_x, double max_x)
{
pcl::visualization::PCLPlotter *plot_line1(new pcl::visualization::PCLPlotter);
// std::vector<double> func1(2, 0);
// func1[0] = c;
// func1[1] = b;
// func1[2] = a;
// plot_line1->addPlotData(func1, point_min.x, point_max.x);
std::cout << "min_x: " << min_x << " max_x: " << max_x << std::endl;
plot_line1->addPlotData(coeff, min_x, max_x);
plot_line1->addPlotData(vector_1, vector_2, "display", vtkChart::POINTS); // X,Y均为double型的向量
plot_line1->setShowLegend(true);
plot_line1->plot();
}
std::vector<Eigen::Vector2d> GeneratePolynomialCurve2D(std::vector<double> &coefficients, Eigen::Vector2d range = Eigen::Vector2d(-10, 10), double step = 0.2)
{
std::cout << "GeneratePolynomialCurve2D" << std::endl;
// for (auto i : coefficients)
// {
// std::cout << i << std::endl;
// }
// std::cout << "range: " << range(0) << " " << range(1) << std::endl;
std::vector<Eigen::Vector2d> points;
points.resize(int((range(1) - range(0)) / step));
double x, y;
for (std::size_t i = 0; i < points.size(); ++i)
{
x = range(0) + step * i;
y = 0;
for (std::size_t j = 0; j < coefficients.size(); ++j)
{
// y = a_0*x^0 + a_1*x^1 + a_2*x^2 + a_n*x^n
y += coefficients[j] * std::pow(x, j);
}
// std::cout << x << " " << y << " ";
points[i] = Eigen::Vector2d(x, y);
}
return points;
}
/// @brief 最小二乘拟合,直接用公式
/// @param data_x
/// @param data_y
/// @param coeff 多项式系数 a_0, a_1, ... a_n
/// @param order 需要拟合的阶数
void PolynomailCurveFit(const std::vector<double> &data_x,
const std::vector<double> &data_y,
std::vector<double> &coeff,
int order
)
{
// Create Matrix Placeholder of size n x k, n= number of datapoints, k = order of polynomial, for exame k = 3 for cubic polynomial
Eigen::MatrixXd X(data_x.size(), order + 1);
Eigen::VectorXd b = Eigen::VectorXd::Map(&data_y.front(), data_y.size());
Eigen::VectorXd A;
// check to make sure inputs are correct
assert(data_x.size() == data_y.size());
assert(data_x.size() >= order + 1);
// Populate the matrix
for (size_t i = 0; i < data_x.size(); ++i)
{
for (size_t j = 0; j < order + 1; ++j)
{
X(i, j) = pow(data_x.at(i), j);
}
}
// std::cout << T << std::endl;
// Solve for linear least square fit
A = (X.transpose() * X).inverse() * X.transpose() * b;
coeff.resize(order + 1);
for (int k = 0; k < order + 1; k++)
{
coeff[k] = A[k];
}
}
/// @brief 最小二乘拟合,用Qr分解
/// @param data_x
/// @param data_y
/// @param coeff 多项式系数 a_0, a_1, ... a_n
/// @param order 需要拟合的阶数
void PolynomailCurveFitQr(const std::vector<double> &data_x,
const std::vector<double> &data_y,
std::vector<double> &coeff,
int order
)
{
// Create Matrix Placeholder of size n x k, n= number of datapoints, k = order of polynomial, for exame k = 3 for cubic polynomial
Eigen::MatrixXd X(data_x.size(), order + 1);
Eigen::VectorXd b = Eigen::VectorXd::Map(&data_y.front(), data_y.size());
Eigen::VectorXd A;
// check to make sure inputs are correct
assert(data_x.size() == data_y.size());
assert(data_x.size() >= order + 1);
// Populate the matrix
for (size_t i = 0; i < data_x.size(); ++i)
{
for (size_t j = 0; j < order + 1; ++j)
{
X(i, j) = pow(data_x.at(i), j);
}
}
// std::cout << T << std::endl;
// Solve for linear least square fit
A = X.householderQr().solve(b);
coeff.resize(order + 1);
for (int k = 0; k < order + 1; k++)
{
coeff[k] = A[k];
}
}
void PrintPolynomailCoeff(const std::vector<double> &coeff, std::string name = "coeff")
{
std::cout << name << ": ";
for (auto i : coeff)
{
std::cout << i << " ";
}
std::cout << std::endl;
}
int main(int argc, char *argv[])
{
std::chrono::high_resolution_clock::time_point all_s = std::chrono::high_resolution_clock::now();
Eigen::Vector2d range = Eigen::Vector2d(-10, 10);
std::vector<double> coeff_gt({
1, 2, 4});
std::vector<double> coeff_fit;
std::vector<double> coeff_fit_qr;
auto points_curve = GeneratePolynomialCurve2D(coeff_gt, range);
std::vector<double> points_x;
std::vector<double> points_y;
// 添加噪声
auto points_curve_noise = GenerateGaussNoise(points_curve, 0, 0.05);
// 不添加噪声
// auto points_curve_noise = points_curve;
for (auto i : points_curve_noise)
{
points_x.push_back(i(0));
points_y.push_back(i(1));
}
PolynomailCurveFit(points_x, points_y, coeff_fit, 2);
PolynomailCurveFitQr(points_x, points_y, coeff_fit_qr, 2);
PrintPolynomailCoeff(coeff_gt, "coeff_gt");
PrintPolynomailCoeff(coeff_fit, "coeff_fit");
PrintPolynomailCoeff(coeff_fit_qr, "coeff_fit_qr");
std::chrono::high_resolution_clock::time_point all_e = std::chrono::high_resolution_clock::now();
auto all_cost = std::chrono::duration_cast<std::chrono::milliseconds>(all_e - all_s).count();
std::cout << "all cost: " << all_cost << " ms" << std::endl;
DisplayLine2D(points_x, points_y, coeff_gt, range(0), range(1));
DisplayLine2D(points_x, points_y, coeff_fit, range(0), range(1));
DisplayLine2D(points_x, points_y, coeff_fit_qr, range(0), range(1));
return 0;
}
CMakeLists.txt
cmake_minimum_required(VERSION 3.18)
project(LeastSquareFitCurve)
find_package(PCL 1.8 REQUIRED)
include_directories(${PCL_INCLUDE_DIRS})
link_directories(${PCL_LIBRARY_DIRS})
add_definitions(${PCL_DEFINITIONS})
add_executable(least_square_fit_curve ./least_square_fit_curve.cpp)
target_link_libraries(least_square_fit_curve ${PCL_LIBRARIES})
compile.bat
cmake -S ./src -B ./build
cmake --build ./build --parallel 8
run.bat
set PATH=D:\carlos\install\PCL 1.10.0\bin;D:\carlos\install\PCL 1.10.0\3rdParty\FLANN\bin;D:\carlos\install\PCL 1.10.0\3rdParty\VTK\bin;D:\carlos\install\PCL 1.10.0\3rdParty\Qhull\bin;D:\carlos\install\PCL 1.10.0\3rdParty\OpenNI2\Tools;%PATH%
.\build\Release\least_square_fit_curve.exe
编译:
cd least_square_fit_curv
./compile.bat
运行
run.bat
注:
其中使用了pcl的曲线绘制,而pcl自带Eigen库,可以使用Open3d和pcl里面提供的Eigen,如果没有pcl和open3d,可以直接安装Eigen,并且把pcl可视化的部分注掉,单独安装Eigen参考:
cmake+Eigen库
qr的参考实现:
最小二乘问题和基于HouseHolder变换的QR分解
使用 C++ Eigen 包的最小二乘多项式拟合
直接矩阵求逆做的代码参考:
3D 空间中拟合曲线
C++/PCL:最小二乘拟合平面直线,平面多项式曲线,空间多项式曲线
C++ 最小二乘法 直线拟合、曲线拟合、平面拟合、高斯拟合
结果
用代码手动生成了二次曲线 f ( x ) = 1 + 2 x + 4 x 2 f(x) = 1+2x+4x^2 f(x)=1+2x+4x2的采样点,不添加噪声的情况下,拟合结果和GT一致
系数:
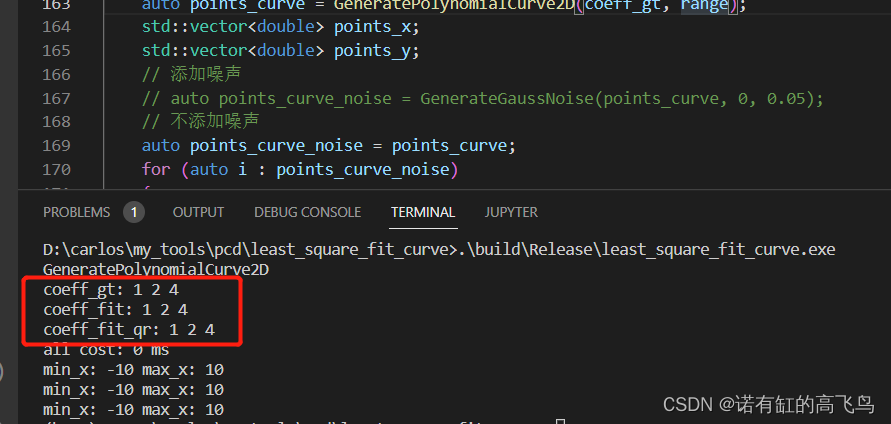
原始点和曲线:
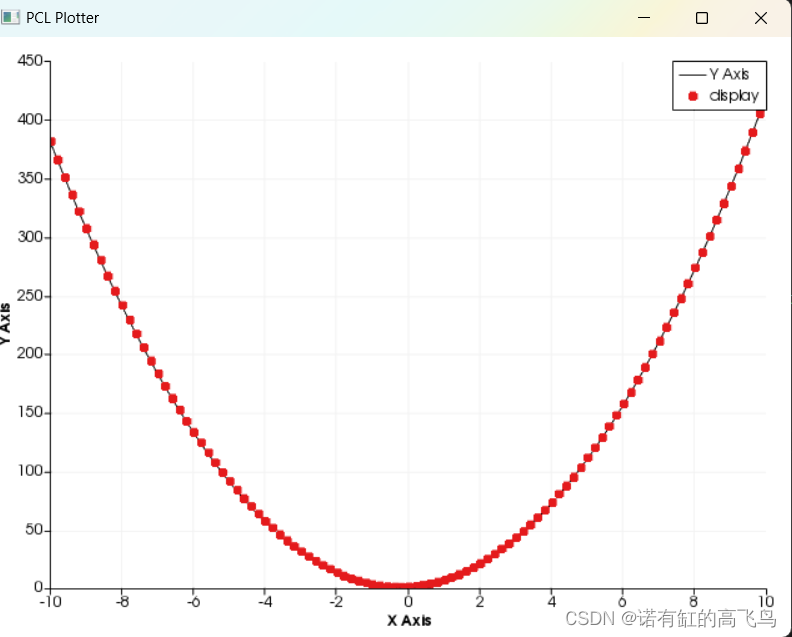 因为系数一致,拟合结果曲线和原始曲线一致,不展示
因为系数一致,拟合结果曲线和原始曲线一致,不展示
添加高斯噪声的情况下:
系数:
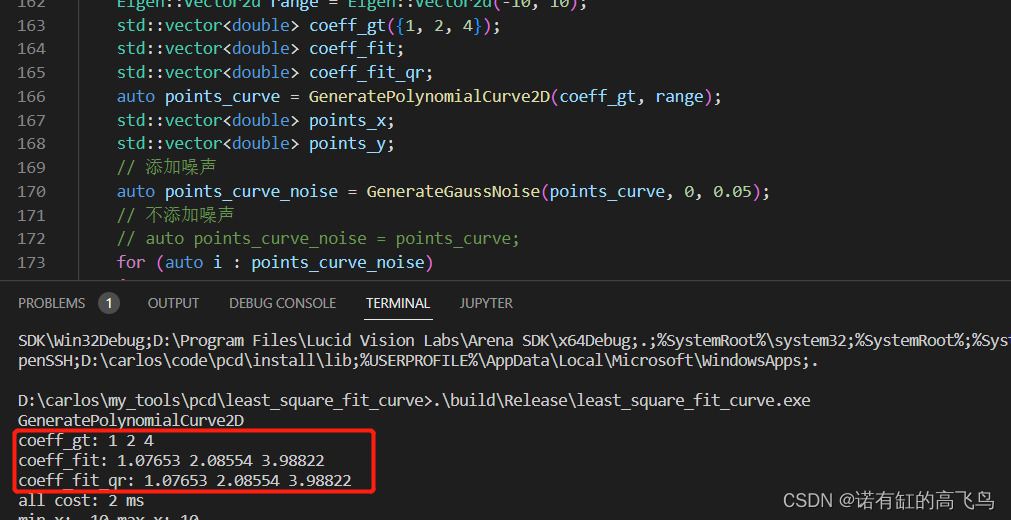
原始点和曲线:
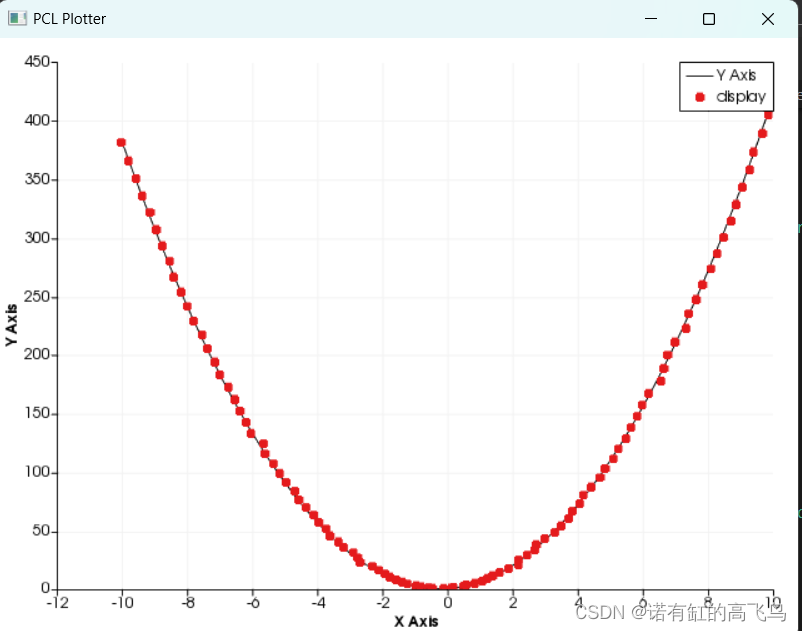
拟合结果曲线:
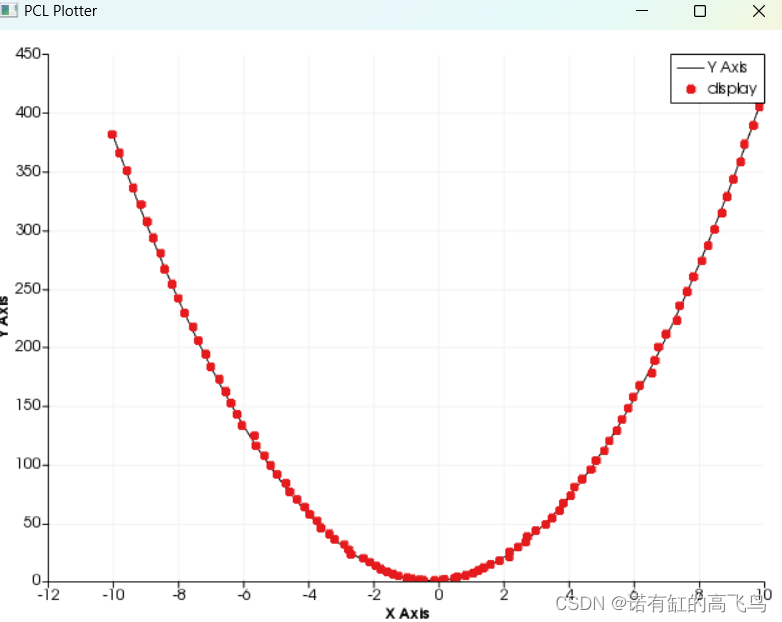
可以看出直接法和qr分解得到的结果是一致的
参考
3D曲线1:多项式曲线 https://zhuanlan.zhihu.com/p/267985141
定方程的求解、最小二乘解、Ax=0、Ax=b的解,求解齐次方程组,求解非齐次方程组(推导十分详细)
生成高斯噪声https://zhuanlan.zhihu.com/p/458994530
其余文中已列出
完
主要做激光/影像三维重建,配准/分割等常用点云算法,技术交流、咨询可私信