交通运输地理空间分析 - 第 1 节课：图与网络

这份文件是我上课的笔记。

严格来讲，因为笔记里面有一半是老师的课件里面的内容，我只是加上了自己的理解和解释在里面，所以这份笔记的内容创作有一半是我老师完成的。

• 这门课程最主要是关于一些地理空间分析的实践方法。
• 比起理论，更关心具体怎么去实现的问题。
• 我自己结合了平常自己经常使用的 Python 来解释和解决问题
• 基于 Jupyter Notebook

在这里分享出来，希望能够帮助到一些人。

课时：32课时（1-16周，8周实验课）

课程要求：

1. 了解交通网络拓扑相关理论知识
2. 掌握地理信息软件（GIS）操作（ mapinfo 等）
3. 具有一定编程能力（ mapbasic 等）

在这份笔记当中，为了熟悉一些实践性的操作方法，我会用 python 做一些示例，包括绘图和一些数据的处理方法。

下面是这份笔记使用的库和的绘图设置：

import numpy as np 
import pandas as pd
import networkx as nx
import matplotlib.pyplot as plt

plt.rcParams.update({
    
    
    # "figure.figsize":(8, 6),
    "font.sans-serif":'SimHei',
    "figure.dpi":100,
    "axes.unicode_minus":False,
    "image.cmap":'viridis'
})

图是最直观的模型

• 图论是交通系统 分析 中的 重要工具
• 图论在交通系统 规划、管理 中 作用大
• 图论是对实际交通网络进行 抽象分析的重要手段

总的来说，图论的方法是对交通网最直观的表述方式。

图论的历史

• 哥尼斯堡七桥问题 (欧拉回路)
• 环球旅行问题(哈密尔顿回路)
• 中国邮路问题

欧拉Euler (1707-1783) 在1736年发表第一篇图论方面的论文，奠基了图论中的一些基本定理

很多问题都可以用点和线来表示，一般点表示实体，线表示实体间的关联

通过计算机解决图论问题

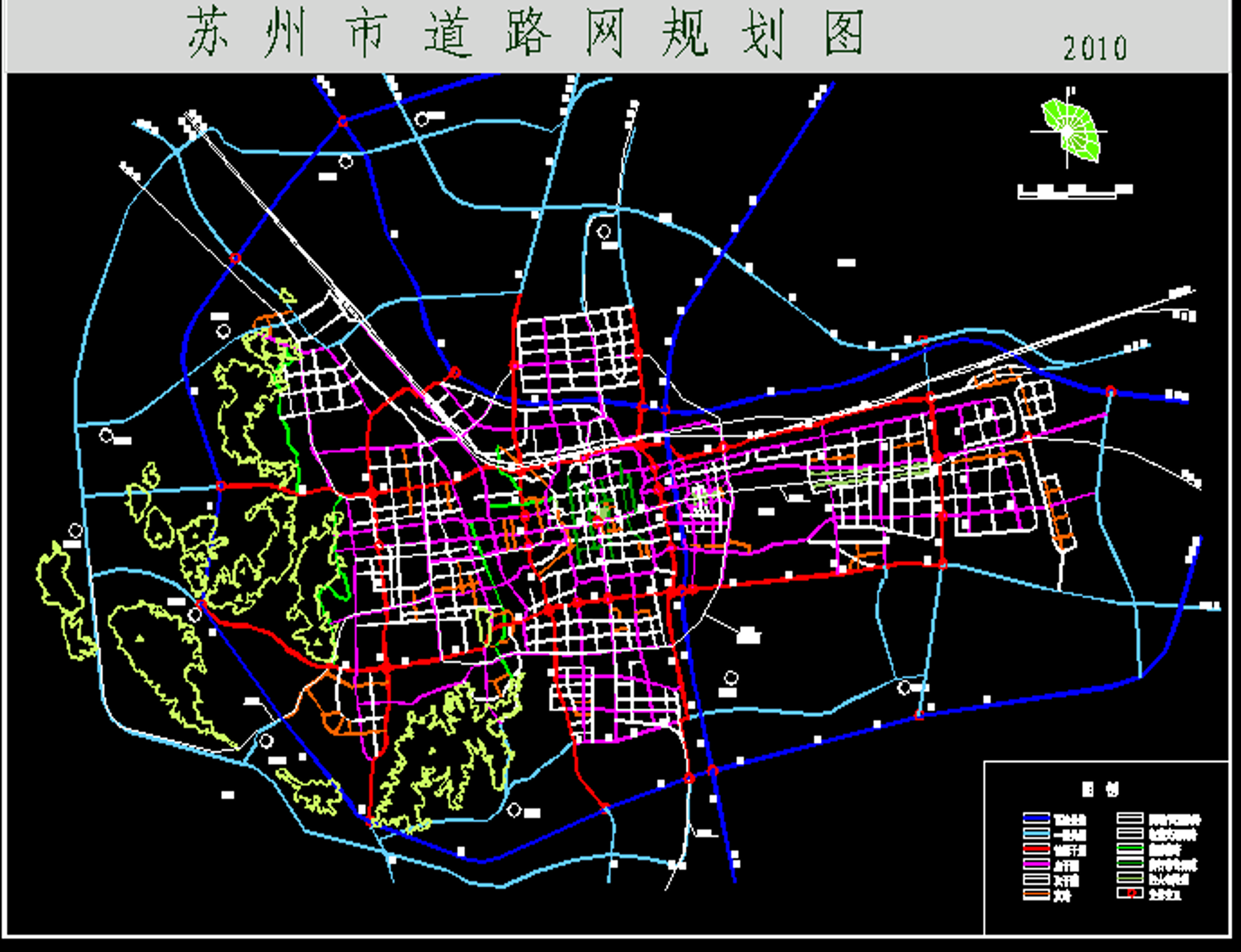
在以往的学习和考试当中，我们之所以可以在短的时间内计算出图问题的结果但这是因为我们的图的规模不够大，所以我们可以用手计算出来。但是如果这个网络的规模足够大，比如下图中这个苏州的路网：

900 多个节点，3000 余条边。

对于这样的问题，人工计算几乎是不可能的。我们就必须依赖计算机。

• 大量的工程计算无法依靠手工完成
• 交通工程中的网络计算必须依靠计算机

大量的工程对象无法研究实物，只能进行抽象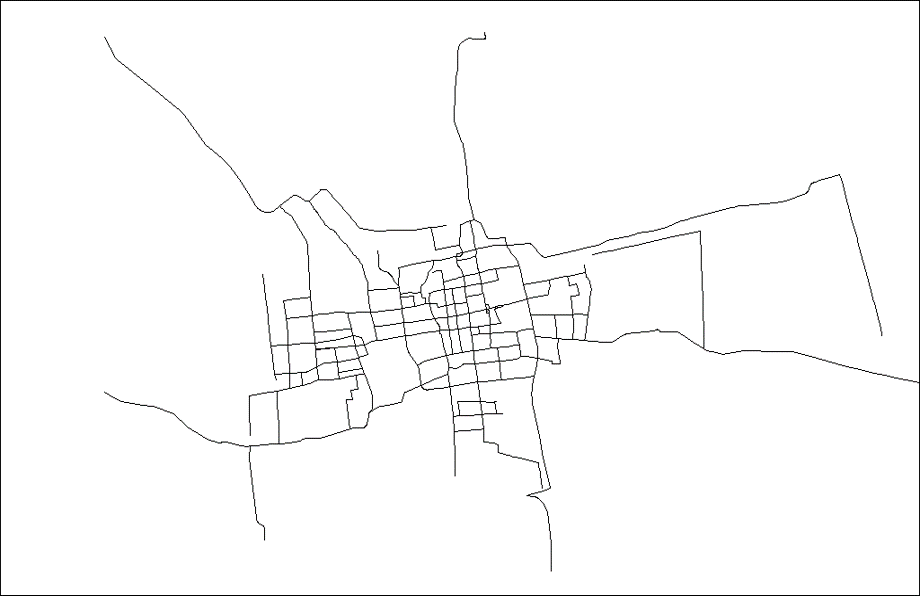

• 道路网、公交线网等

比如对于上面的苏州市路网结构图，我们就能进行如下的抽象，产生新的结构图：

如果在图中，细微的小的道路网也表现出来，机动车、非机动车都包含在内。

在这种情况下，交通工程中所使用的图的规模呈现几何倍数的增长。这就越发体现出计算机在解决图论问题中的重要性。

图论概述

在其他课程上面我们会详细讲到图论的问题，所以这里只是简单的一笔带过。

图论在计算机中的表达方法

这里介绍 5 种最简单的形式。

1. 关联矩阵法

对于一个给定的图，构造关联矩阵 $A_{a_{i,j}}$ ，有：

$$a_{i,j}=\{\begin{array}{l}1,边e_j与点V_i相关联\\ 0,否则\end{array}$$

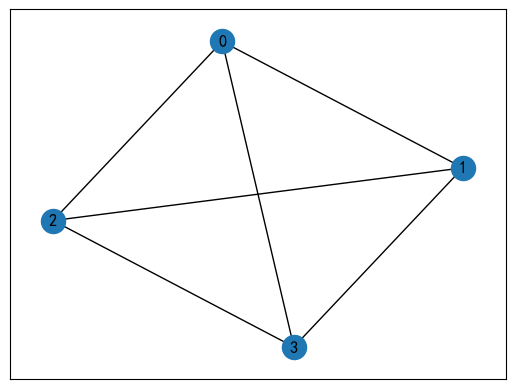
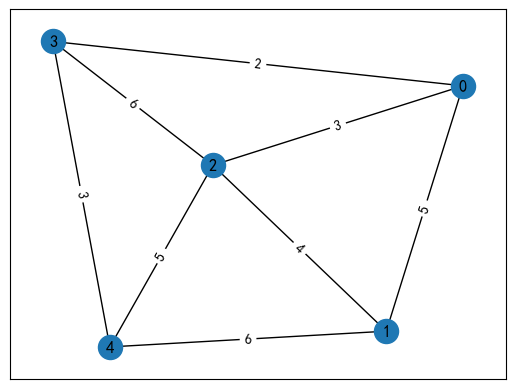
比如对于这样的一个网络图：

这个图形总共有六条边、四个顶点。顶点和边的关系可以表示为：

节点/边	e1	e2	e3	e4	e5	e6
V1	接邻	不接邻	接邻	接邻	不接邻	不接邻
V2	接邻	接邻	不接邻	不接邻	接邻	不接邻
V3	不接邻	接邻	接邻	不接邻	不接邻	接邻
V4	不接邻	不接邻	不接邻	接邻	接邻	接邻

用 0 表示 不接邻，用 1 表示 接邻，则我们可以构造如下的关联矩阵：

$$A=\left[\begin{array}{cccccc}1& 0& 1& 1& 0& 0\\ 1& 1& 0& 0& 1& 0\\ 0& 1& 1& 0& 0& 1\\ 0& 0& 0& 1& 1& 1\end{array}\right]$$

如果想再 Python 中来实现，则需要利用 numpy 把关联矩阵转化为接邻矩阵。我们定义一个函数 im2am 来实现这个功能：

def im2am( im ):
    import numpy as np
    am = (np.dot( im, im.T) > 0).astype(int)
    np.fill_diagonal(am, 0)
    return am

这段代码的原理如下：

对于关联矩阵 A，存在如下的性质：关联矩阵乘以自身转置的积等于邻接矩阵，但是对角线元素全为 1。即：

$$A\times A^T=D_{(Diag=1)}$$

只要再给对角线元素赋值 0，即可得到邻接矩阵。

• np.dot(im, im.T)：这一步是将关联矩阵 im 与其转置矩阵相乘，得到一个新的矩阵。这个操作实际上是计算每个节点之间的连接数量，也就是节点之间存在多少条边。
• > 0：通过比较操作符 > 将上一步得到的矩阵中大于零的元素置为 True，小于等于零的元素置为 False。这样可以得到一个布尔类型的矩阵，表示节点之间是否有连接。
• .astype(int)：将布尔类型的矩阵转换为整数类型的矩阵，True 转换为 1，False 转换为 0。这样就得到了邻接矩阵 am。
• np.fill_diagonal(am, 0)：将邻接矩阵 am 的对角线元素（自身与自身的连接）设置为 0。在网络计划图中，通常不考虑节点与自身存在连接。

（如果不知道什么是邻接矩阵，就继续往下看，下面会讲到。）

im = np.array(
   [ 
      [ 1, 0, 1, 1, 0, 0 ], 
      [ 1, 1, 0, 0, 1, 0 ], 
      [ 0, 1, 1, 0, 0, 1 ], 
      [ 0, 0, 0, 1, 1, 1 ] 
    ] 
  )

# 转换为邻接矩阵
am = im2am( im )
G = nx.from_numpy_array(am)

# 调整图的元素分布位置为放射状分布
# 这样好看
pos = nx.spring_layout(G)

# 绘图
nx.draw_networkx(
  G, 
  pos, 
  with_labels = True
  )

2. 邻接矩阵法

最直观的一种形式，只表示节点之间的邻接关系。表达逻辑如下：

$$d_{i,j}=\{\begin{array}{l}1,节点i和节点j有边相邻\\ 0,否则\end{array}$$

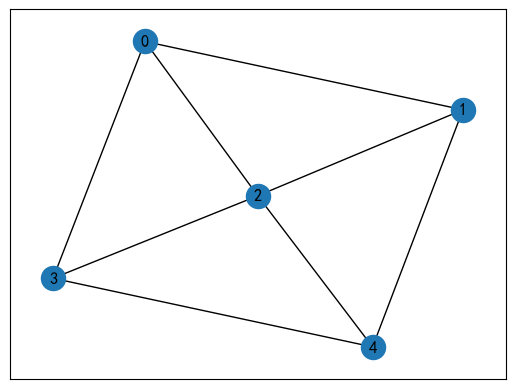
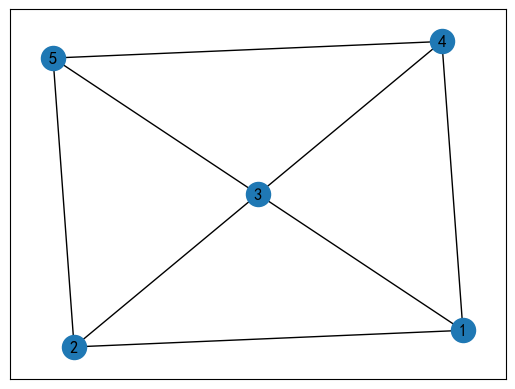
假如现在存在如下网络计划图：

我们可以写出这样一张表。

	v1	v2	v3	v4	v5
v1	不接邻	接邻	接邻	接邻	不接邻
v2	接邻	不接邻	接邻	不接邻	接邻
v3	接邻	接邻	不接邻	接邻	接邻
v4	接邻	不接邻	接邻	不接邻	接邻
v5	不接邻	接邻	接邻	接邻	不接邻

用 0 表示 不接邻，用 1 表示 接邻，则我们可以构造如下的邻接矩阵：

$$D=\left[\begin{array}{ccccc}0& 1& 1& 1& 0\\ 1& 0& 1& 0& 1\\ 1& 1& 0& 1& 1\\ 1& 0& 1& 0& 1\\ 0& 1& 1& 1& 0\end{array}\right]$$

adj_mat = np.array(
    [ [ 0, 1, 1, 1, 0 ],
      [ 1, 0, 1, 0, 1 ],
      [ 1, 1, 0, 1, 1 ],
      [ 1, 0, 1, 0, 1 ],
      [ 0, 1, 1, 1, 0 ] ]
  )
G = nx.from_numpy_array(adj_mat)

pos = nx.spring_layout(G)
nx.draw_networkx(G, pos, with_labels = True)

3. 权重矩阵法

这种表达方式可以把各个节点的边的权重都表示出来。表示逻辑如下：

$$W_{ij}=\{\begin{array}{l}0,i=j\\ \infty ,无边连接\\ w_{ij},i,j有边连接\end{array}$$

同样，我们还用上面这张图来举例子。我们可以用下面的表格来表示边和边之间的权重：

（对于不接邻的节点，我们用 $\infty$ 来表示两个节点之间没有接邻性。）

	v1	v2	v3	v4	v5
v1	0	5	3	2	$\infty$
v2	5	0	4	0	6
v3	3	4	0	6	5
v4	2	$\infty$	6	0	3
v5	$\infty$	6	5	3	0

同样，我们写出矩阵：

$$W_{ij}=\left(\begin{array}{ccccc}0& 5& 3& 2& \infty \\ 5& 0& 4& 0& 6\\ 3& 4& 0& 6& 5\\ 2& \infty & 6& 0& 3\\ \infty & 6& 5& 3& 0\end{array}\right)$$

注意，在 Python 的 NetworkX 中调用 networkx.from_numpy_array() 的时候，$\infty$ 项是表述为 0 的，程序会自动把不同节点之间的 0 识别为 “这条边不存在”，相同节点之间的 0 视作 “自身无环”。不需要设置 float("inf") 或者 np.inf。

但是如果使用 MatLab，就要设置 inf 项。

如果矩阵是从别的什么地方读取的，可以通过下面的设置来替换数据里的 inf：

inf_Index = np.isinf(mat)
mat[inf_Index] = 0

np.isinf() 也可换成 np.isnan() 来替换 NaN 项。

weight_Mat = np.array(
        [
            [ 0, 5, 3, 2, 0 ],
            [ 5, 0, 4, 0, 6 ],
            [ 3, 4, 0, 6, 5 ],
            [ 2, 0, 6, 0, 3 ],
            [ 0, 6, 5, 3, 0 ] 
        ]
    )
G = nx.from_numpy_array(weight_Mat)
pos = nx.spring_layout(G)
nx.draw_networkx(
    G, 
    pos, 
    with_labels = True
    )

# 添加边权绘制的代码
weights = nx.get_edge_attributes(G, "weight")
nx.draw_networkx_edge_labels(
    G, 
    pos, 
    edge_labels = weights,
    font_size = 10
    )

{(0, 1): Text(0.8240830791193997, -0.07520386993244665, '5'),
 (0, 2): Text(0.4262223244243833, 0.3588472968939219, '3'),
 (0, 3): Text(0.059674025608137726, 0.6825840310753251, '2'),
 (1, 2): Text(0.2503054035437831, -0.28291466322645287, '4'),
 (1, 4): Text(0.014103649967479648, -0.7581522828752834, '6'),
 (2, 3): Text(-0.5141036499674789, 0.47487323778131885, '6'),
 (2, 4): Text(-0.38375710472753677, -0.3241011160489147, '5'),
 (3, 4): Text(-0.7503054035437824, -0.0003643818675115873, '3')}

4. 边目录法

把所有出现的边全都用一个目录写出来。

$$\begin{gathered} e_1=(1,2) \\ {e}_2=(2,5) \\ {e}_3=(5,4) \\ {e}_4=(1,4) \\ \cdots \end{gathered}$$

太简单我就不解释了。

在 NetWorkX 里面使用这种方法的时候理论上可以通过字典的设置方法来带上各个边的权重。我这里为了省事就不写了。

G = nx.Graph()
G.add_edges_from(
        [
            [1, 2], [1, 3], [1, 4],
            [2, 3], [2, 5], 
            [3, 4], [3, 5], 
            [4, 5]
        ] 
    )
pos = nx.spring_layout(G)
nx.draw_networkx( G, pos, with_labels = True )

5. 邻接目录法

• 计算机存储效率达到最高，是这里最推荐的方法。

节点号	V(1)：相邻节点数	N(i, j) 相邻节点号
1	2	2, 5
2	3	1, 3, 4
3	2	2, 6
4	3	2, 5, 6
5	3	1, 4, 6
6	3	3, 4, 5

不过这个东西可以不用太关注，只要知道有这么一种形式就好了。我们不是搞计算机专业的，所以大可不用管。因为它不是写给人看的。

换句话说，我拿 Python 演示一下：如果用 networksx.readwrite.adjlist.read_adjlist() 将上面的 G 写入文件

nx.readwrite.adjlist.write_adjlist(
    G,
    "./data/grid.adjlist",
    delimiter = ' ',
    encoding = 'utf-8'
    )

然后我们可以看见文件内是这样的形式：

#D:\Python\Python39\Lib\site-packages\ipykernel_launcher.py --ip=127.0.0.1 --stdin=9003 --control=9001 --hb=9000 --Session.signature_scheme="hmac-sha256" --Session.key=b"db53af50-2b8e-41ac-af10-4983cfca115a" --shell=9002 --transport="tcp" --iopub=9004 --f=c:\Users\asus\AppData\Roaming\jupyter\runtime\kernel-v2-17676oxNCvWsMPa4f.json
# GMT Thu Aug 24 08:40:59 2023
# 
1 2 3 4
2 3 5
3 4 5
4 5
5

这些内容显然不是写给人看的。不过我们还是可以看得出来，这里的信息是从左向右写的，最左边的一列是节点的编号，右边依次排开，用分隔符分开。

象征性地写一下，把上面的表格写入一个 forRead.adjlist：

1 2 5
2 1 3 4
3 2 6
4 2 5 6
5 1 4 6
6 3 4 5

运行下面的代码就能看见图。

G = nx.readwrite.adjlist.read_adjlist(
    "./data/forRead.adjlist",
    delimiter = ' ',
    encoding = 'utf-8'
    )
pos = nx.spring_layout(G)
nx.draw_networkx( G, pos, with_labels = True )

p.s. 这里说一下，就是我尝试过利用 pandas 库的一些功能把上面的 adjlist 储存为 .csv 文件，并且读取为我们熟悉的 DataFrame 二维表的形式，三列分别为节点、与节点邻接的其他节点的数量和邻接目录。但是没有成功。遇到的各种问题我就不多赘述了，反正基本上可以肯定这个东西设计出来就不是给人读的。

一些交通运输上的概念的复习

路段

• 路段是一个边和其两头节点的组合

• 路段是区域交通网络的最基本单元

定义：某种交通运输方式下的某个不受交通工程影响的一个独立的可以进行交通行为的一个边。

路径：是由一个或者很多的路段构成的

运输通道

交通运输通道定义：由起讫点相同，且中途主经由大体相同的绪路径所组成的交通运输带(走廊) 。

运输大通道：在主要客、货流方向上配置有强大交通运输系统的运输通道。

• 一条双向六车道的高速公路
• 一条双线自动闭塞的干线铁路
• 相当的水运通道、管道

通道可能是一个以上的路径并列形成的。

枢纽

是在两条或者两条以上交通线路的交汇、衔接处形成的，具有交通组织、交通中转、交通交换以及部分或者全部交通运输辅助的装卸、仓储、信息服务；及其它辅助服务功能的综合性设施。

我国比较著名的交通枢纽有上海的虹桥，既是机场又是火车、高铁站；还有著名的南京南站。

城市常见的立体交叉口，也属于交通枢纽。

两种典型的网络

1. 点 - 点式网络
2. 轴辐式网络

点 - 点式网络：没有枢纽。

轴辐式网络：分为单枢纽或者多枢纽

相比点 - 点式网络，轴辐式网络的优点在于节约很多不需要开放的线路，可以把流集中到一点。

fig, axes = plt.subplots(
        1, 3,
        figsize = (15,5)
    )

# 点 - 点式网络
Gra_A = nx.Graph()
Gra_A.add_nodes_from([1, 2, 3, 4, 5])
Gra_A.add_edges_from([
    [1, 2], [1, 3], [1, 4], [1, 5],
    [2, 3], [2, 4], [2, 5],
    [3, 4], [3, 5], 
    [4, 5] ]
) 
axes[0].set_title('点 - 点式网络')
nx.draw_networkx( Gra_A, with_labels = True, ax = axes[0] )

# 单枢纽网络式网络
Gra_B = nx.Graph()
Gra_B.add_nodes_from([1, 2, 3, 4, 5])
Gra_B.add_edges_from([
    [1, 5],
    [2, 5],
    [3, 5], 
    [4, 5] ]
) 
axes[1].set_title('单枢纽网络式网络')
nx.draw_networkx( Gra_B, with_labels = True, ax = axes[1] )

# 多枢纽网络式网络
Gra_C = nx.Graph()
Gra_C.add_nodes_from([1, 2, 3, 4, 5, 6, 7, 8])
Gra_C.add_edges_from([
    [1, 4], [2, 4], [3, 4],
    [4, 5], 
    [5, 6], [5, 7], [5, 8], ]
) 
axes[2].set_title('多枢纽网络式网络')
nx.draw_networkx( Gra_C, with_labels = True, ax = axes[2] )

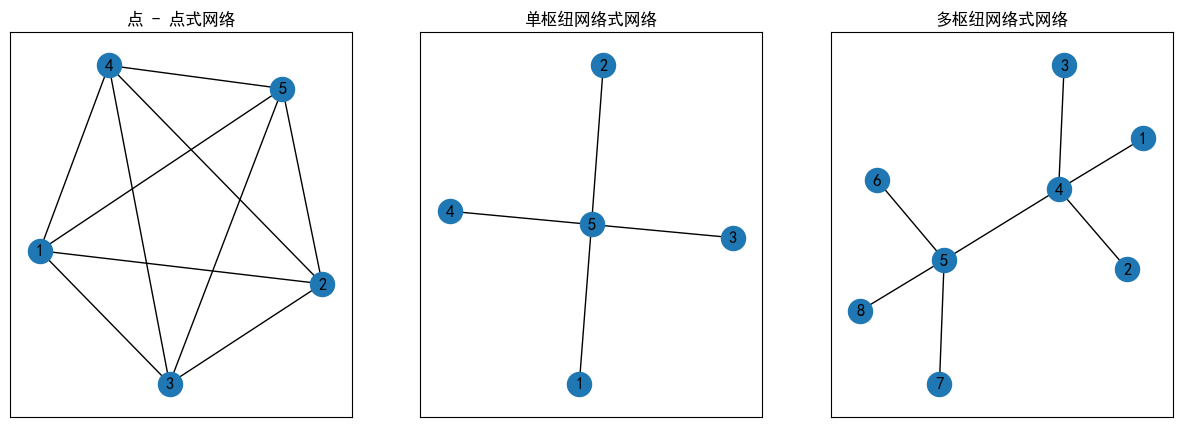
交通网结构

现实的交通运输网的不可避免地要对交通网进行 一定程度的简化、假设和抽象描述

• 详尽的交通网络：即近乎完全按照现实网络进行表示和绘制，内容全，但可能表示和分析较为困难。对于宏观网络或者小区域网络适用。
• 逻辑网络：对实际网络进行功能性、或者结构关系的简化，得到抽象逻辑性网络，其中的节点和边主要代表交通逻辑关系。
  • 功能性、可达性网络：属于逻辑网络的一种，用于对区域部分性能的分析。
• 结构网络：仅仅模拟区域交通的结构，进行辅助性的管理使用。
• 参数网络：仅仅对主要参数进行抽取，一般更适用于规划或者管理方面。

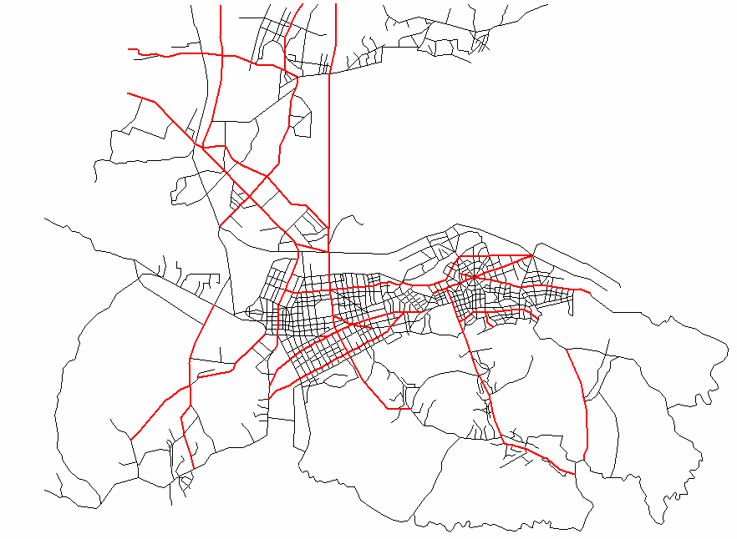
下图展示了经过简化的大连主干道路网。这个图是用 MapInfo 画的。

复杂网络理论及其应用

我们学校很多教授都在搞这个，写了很多质量很高的 SCI 论文。

• 小世界实验：六度分离、Erdos数、bacon数等
• 一些实际的复杂网络系统：Web、科学家合作网络、经济网络、交通网络、疾病传播等
• 复杂网络的静态几何量：度分布、聚类系数、平均路径长度等
• 网络拓扑的基本模型及其性质：随机网络、Small World网络、Scale Free网络等

近几年的研究态势：发展历程、会议、论文、软件、实证等

六度分离

我们会不会有这样的经历：半夜看朋友圈的时候，发现自己的室友给自己的小学同学点了个赞。一问才发现几年前两个人参加了某个活动，早就认识了。感叹世界多么小！

我们或许有过这样的经历：偶尔碰到一个陌生人，同他聊了一会后发现你认识的某个人居然他也认识，然后一起发出 “这个世界真小” 的感叹。那么对于世界上任意两个人来说，借助第三者、第四者这样的间接关系来建立起他们两人的联系平均来说最少要通过多少人呢？

美国社会心理学家斯坦利•米尔格伦(Stanley Milgram)在1967年通过一些实验后得出结论：中间的联系人平均只需要5个。他把这个结论称为 “六度分离” (six degrees of separation)。

六度分离: 平均只要通过5个人，你就能与世界任何一个角落的任何一个人发生联系。这个结论定量地说明了我们世界的”大小”，或者说人与人关系的紧密程度。

30多年来，六度分离理论一直被作为社会心理学的经典范例之一。

尽管如此，实际上这个理论并没有得到严格的证实。美国心理学教授朱迪斯•克兰菲尔德(Judith Kleinfeld)对米尔格伦最初的实验提出不同意见，因为她发现实验的完成率极低。

实验的步骤：

1. 首先把志愿者交给 A，告诉他要把信件送给 S
2. 如果他不认识 S，可以先把信件交给他认识的朋友 B，B 是他认为最可能认识 S 的人
3. B 把信件转递给其他人
4. 如果统计样本中的多个 A 到 S 只有 6 次传递，那么结论成立。

然而，在这个实验中，实际上只有三分之一的信送到了收信人那里，因此实验的完成率很低。

但是试验数据表明世界确实比我们想象的要小！

小世界实验

Paul Erdos ( (1913-1996)， 出生于匈牙利的犹太籍数学家，被公认为本世纪最伟大的天才之一。

Erdos毕生发表的论文超过1500篇（在数学史上仅次于欧拉 (Euler ，1707-1783) )，超长的合作者名单,合作者超过450位。但若加上别人所做，但曾获他关键性的提示之论文，则他的论文应有数万篇。

他的研究领域主要是数论和组合数学，但他的论文中涵盖的学科有逼近论、初等几何、集合论、概率论、数理逻辑、格与序代数结构、线性代数、群论、拓扑群、多项式、测度论、单复变函数、差分方程与函数方程、数列、Fourier 分析、泛函分析、一般拓扑和代数拓扑、统计、数值分析、计算机科学、信息论等等。

“Mathematical Reviews” 曾把数学划分为大约六十个分支，Erdos的论文涉及到了其中的 40%.

数学家以下述方式来定义 Erdos 数 (Erdos number) : Erdos 本人之 Erdos 数为 0，任何人若曾与 Erdos 合写过论文，则其 Erdos 数为 1。任何人若曾与一位 Erdos 数为 l (且不曾与有更少的 Erdos 数) 的人合写过论文， 则他的 Erdos 数为 2

几乎每一个当代数学家都有一个有限的 Erdos 数，而且这个数往往非常小，小得出乎本人的预料。比如说证明 Fermat 大定理的 Andrew Wiles，他的研究方向与 Erdos 相去甚远，但他的 Erdos 数只有 3，是通过这个途径实现的：

• Fields 奖得主的 Erdos 数都不超过 5,（只有 Cohen 和 Grothendieck 的 Erdos 数是 5）
• Nevanlinna 奖得主的 Erdos 数不超过 3，（只有 Valiant 的 Erdos 数是 3）
• Wolf 数学奖得主的 Erdos 数不超过 6，（只有 V.I.Arnold 是 6，且只有 Kolmogorov 是 5，）
• Steele 奖的终身成就奖得主的 Erdos 数不超过 4.

在具有有限 Erdos 数的人名单中往往还能发现一些其他领域的专家，如: 比尔盖兹(Bill Gates)， 他的 Erdos 数是4，通过如下途径实现：

爱因斯坦是2.

Kavin Bacon

贝肯数来源于一个好莱坞游戏，这个游戏要求参与者们尝试用各种方法，把某个演员和凯文·贝肯这个美国好莱坞演员有联系，并且尽可能减少中间的环节。

想方设法把好莱坞的每个演员用最多六步把他们的娱乐圈关系与演员凯文贝肯联系起来。当作为一个游戏，玩家必须尽量以最少的步骤连接男女演员和凯文贝肯关系。男女演员的贝肯数是他们与凯文贝肯来往关系程度。某个演员他或她的数字越大，那么他们离凯文的关系和来往就越远。

凯文在比赛中得了 0 名。一个在电影里和他一起工作的演员会有第一名。如果一个演员和另一个演员直接与凯文合作过的演员合作，他就会排在第二名，以此类推。只有12%的演员无法定义数字，如果得出这样的结果就说明他们无法任何方式与凯文联系在一起。

凯文贝肯起初并不喜欢这个游戏，但后来他发现有那么多娱乐圈的演员可以和他联系在一起，他觉得不可思议。凯文贝肯曾出演过许多电影，并与许多著名演员合作过。一个演员的本肯数越小那他们就可以有多出名。此外，与凯文一起编导电影的编剧，作家和工作人员的其他人也可以使用贝肯数，凯文他出演过许多好莱坞的好电影里，所以一个演员的贝肯数越小，他就越出名。

发现: 在曾经参演的美国电影演员中，没有一个人的 Bacon 数超过 4

在网上有一个网页 The Oracle of Bacon。网站的数据库里总共存有有 783940 个世界各地的演员的信息以及 231, 088 部电影信息。

通过简单地输入演员名字就可以知道这个演员的 bacon 数。

目前比如输入 Stephen Chow（周星驰）就可以得到这样的结果：周星驰在 1991 (Haomen yeyan) 》 中与洪金宝 (Sammo Hung Kam-Bo) 合作；而洪金宝又在李小龙的最后一部电影，即 1978 年的《死亡的游戏 （Game of Death）》 中与 Colleen Camp 合作；Colleen Camp 在去年的电影《Trapped》 中与 Kevin Bacon 合作。这样周星驰的培根数为 3。

对所有这将近 78 万个演员所做的统计。结果如下所示: 左边是 Bacon 数，右边是拥有这个 Bacon 数的演员个数。可以看到最大的培根数仅仅为 8。平均培根数仅为 2.948。

Kevin Bacon Number	# of prople
0	1
1	1962
2	171652
3	485636
4	115701
5	8124
6	779
7	72
8	13

Kavin Bacon图

• 有明确的定义（顶点和边）
• 数据库中 90% 的演员被归入到一个单独的连通分支
• 最高的有限 Bacon 数为 8

平均 Bacon 数为 2.9

注：少数演员承担了将多数演员联系在一起的工作。

这些内容体现了网络的重要的普遍性质，就是 连接作用往往仅由少数的节点承担！

网络

网络是一个包含了大量个体及个体之间相互作用的系统

任何一个网络可以抽象为一个图.（最早可追溯到 Euler 对 Konogsberg 七桥问题的研究）

网络的拓扑性质：网络不依赖于节点的具体位置和边的具体形态就能表现出来的性质。

图的分类: 无向图, 有向图,加权图, 混合图

简单图是指: 无向, 无权, 无重边, 无自环的图

目前关于简单网络的研究结果较多

在本课程中我们只关心简单图。