整数规划Python

整数规划

纯整数规划：所有决策变量都限定为整数

混合整数规划：仅一部分变量限定为整数

0-1整数规划：决策变量仅限于0或1

1.整数规划问题与求解

import cvxpy as cp
from numpy import array
c=array([40,90])  #定义目标向量
a=array([[9,7],[-7,-20]])  #定义约束矩阵
b=array([56,-70])  #定义约束条件的右边向量
x=cp.Variable(2,integer=True)  #定义两个整数决策变量
obj=cp.Minimize(c*x)  #构造目标函数
cons=[a*x<=b, x>=0]    #构造约束条件
prob=cp.Problem(obj, cons)  #构建问题模型
prob.solve(solver='GLPK_MI',verbose =	True)  #求解问题
print("最优值为:",prob.value)
print("最优解为：\n",x.value)

2.指派问题

许多实际应用问题可以归结为这样的形式：将不同的任务分派给若干人去完成，由于任务的难易程度以及人员的素质高低不尽相同，因此每个人完成不同任务的效率存在差异。于是需要考虑应该分派何人去完成哪种任务能够使得总效率最高。这一类问题通常称为指派问题。

2.1标准指派模型

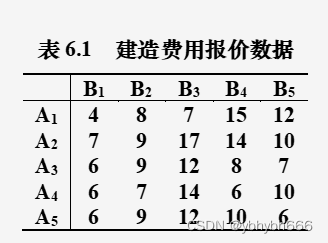
某商业公司计划开办5家新商店，决定由5家建筑公司分别承建。已知建筑公司 （ ）对新商店 （ ）的建造费用报价（万元）为 （ ），见表6.1。为节省费用，商业公司应当对5家建筑公司怎样分配建造任务，才能使总的建造费用最少？

import cvxpy as cp
import numpy as np
c=np.array([[4, 8, 7, 15, 12],
         	[7, 9, 17, 14, 10],
	        [6, 9, 12, 8, 7],
   	     	[6, 7, 14, 6, 10],
        	[6, 9, 12, 10, 6]])
x = cp.Variable((5,5),integer=True)
obj = cp.Minimize(cp.sum(cp.multiply(c,x)))
con= [0 <= x, x <= 1, cp.sum(x, axis=0, keepdims=True)==1,
             cp.sum(x, axis=1, keepdims=True)==1]
prob = cp.Problem(obj, con)
prob.solve(solver='GLPK_MI')
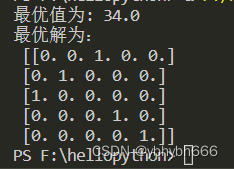
print("最优值为:",prob.value)
print("最优解为：\n",x.value)

2.2 人数或者任务不匹配的指派问题

2.3一个人可完成多项任务的指派问题

一些指派问题中，可能出现要求某人完成几项任务的情形。对于这样的指派问题，可将该人看作相同的几个人来接受指派，只需令其完成同一项任务的效率都一样即可。

2.4某项任务一定不能由某人完成的指派问题。

一些指派问题中，可能出现某人不能完成某项任务的情形。对于这样的指派问题，只需将相应的效率值（成本型）取成足够大的数即可。

3.装箱问题

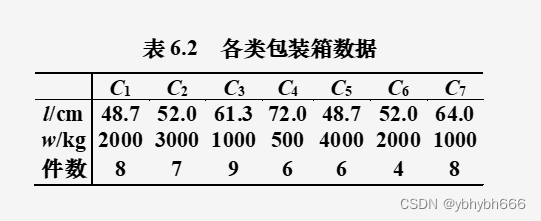
解 这是美国大学生数学建模竞赛1988年B题。题中所有包装箱共重89t，而两辆平板车一共只能载重80t，因此不可能全装下。究竟在两辆车上各装哪些种类箱子且各为多少才合适，必须有评价的标准。这标准就是遵守题中说明的重量、厚度、件数等方面的约束条件，尽可能地多装，而尽可能多装有两种理解：一是尽可能在体积上多装，由于规定是按面包片重叠那样的装法，故等价于尽可能使两辆车上的装箱总厚度尽可能大；二是尽可能在重量上多装，即使得两辆车上的装箱总重量尽可能大。



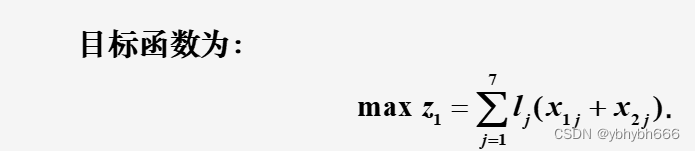
所以最终得到数学模型

import cvxpy as cp
import numpy as np
L=np.array([48.7,52.0,61.3,72.0,48.7,52.0,64.0])	
w=np.array([2000,3000,1000,500,4000,2000,1000])
a=np.array([8,7,9,6,6,4,8])
x=cp.Variable((2,7), integer=True)
obj=cp.Maximize(cp.sum(x*L))
con=[cp.sum(x,axis=0,keepdims=True)<=a.reshape(1,7),
	 x*L<=1020, x*w<=40000, cp.sum(x[:,4:]*L[4:])<=302.7, x>=0]
prob = cp.Problem(obj, con)
prob.solve(solver='GLPK_MI',verbose =True)
print("最优值为:",prob.value)
print("最优解为：\n",x.value)

最优值为: 2039.4
最优解为：
[[4. 1. 5. 3. 3. 2. 0.]
[4. 6. 4. 3. 0. 1. 0.]]

二、非线性规划

1 非线性规划概念和理论

1.1. 非线性规划模型

非线性规划模型的一般形式描述如下：

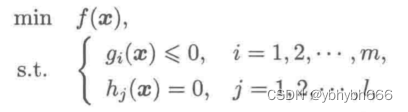
采用向量表示法写作：

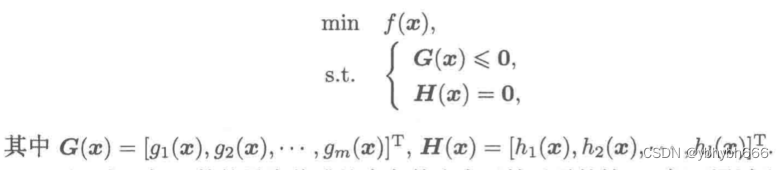
如果遇到求目标函数最大值或者约束条件大于0的情况都可以通过取相反数转化为一般形式。

定义6.1：严格全局最优解和严格局部最优解

需要注意的是：线性规划的最优解一定在边界取到，特别是可行域顶点上达到。但是非线性规划没有这个特征。最优解（如果存在）可能在可行域任意一点达到 。一般非线性规划算法给出的也只能是局部最优解，不能保证是全局最优解。

2.2 无约束非线性规划的求解

无约束线性规划问题可以具体表示为：

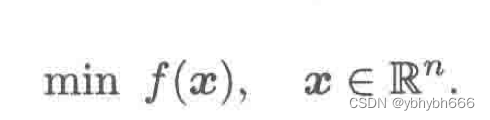
该类问题可以借鉴高等数学中二元函数求极值的方法。首先引入下面的定理：



常用方法有：最速降线法，牛顿法和拟牛顿法，这里不详细介绍了

2.3. 有约束非线性规划的求解

比较常见的处理思路：可能的话将非线性问题转化为线性问题，将约束问题转化为无约束问题。

(1)求解有等式约束非线性规划的lagrange乘数法

对于特殊的只有等式约束的非线性规划问题的情形


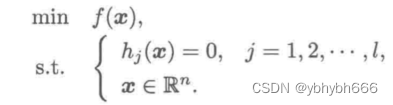
这样可以把问题求解转化为无约束问题求解

（2）求解有约束非线性规划的罚函数法
罚函数法
注：罚函数法计算精度较差，除非要求算法达到实时，否则一般不用

2. 非线性规划的python求解

2.1用scipy.optimize模块的minimize函数求解

求解非线性规划问题

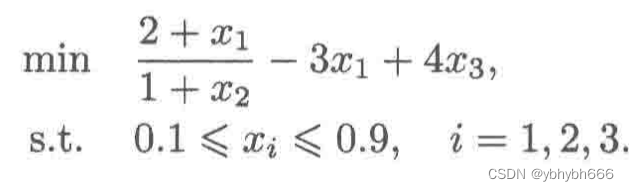
from scipy.optimize import minimize
from numpy import ones
def obj(x):
	x1,x2,x3=x
	return (2+x1)/(1+x2)-3*x1+4*x3
LB=[0.1]*3; UB=[0.9]*3
bound=tuple(zip(LB, UB))   #生成决策向量界限的元组
res=minimize(obj,ones(3),bounds=bound) #第2个参数为初值
print(res.fun,'\n',res.success,'\n',res.x)  #输出最优值、求解状态、最优解

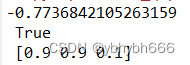
所以：最优解为x1=x2=0.9,x3=0.1，目标函数的最优值为-0.7737

求解下列非线性规划问题

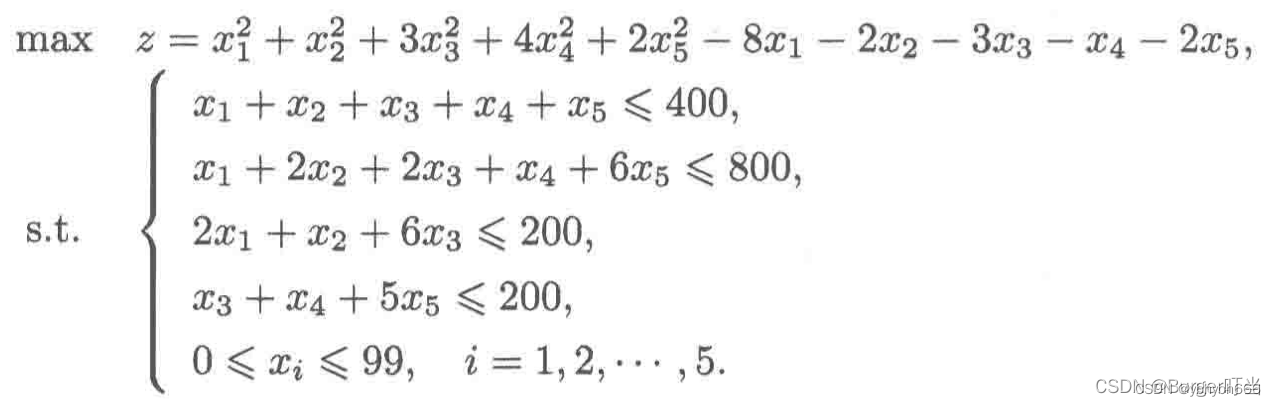
from scipy.optimize import minimize
import numpy as np
c1=np.array([1,1,3,4,2]); c2=np.array([-8,-2,-3,-1,-2])	
A=np.array([[1,1,1,1,1],[1,2,2,1,6],
	        [2,1,6,0,0],[0,0,1,1,5]])
b=np.array([400,800,200,200])
obj=lambda x: np.dot(-c1,x**2)+np.dot(-c2,x)
cons={'type':'ineq','fun':lambda x:b-A@x}
bd=[(0,99) for i in range(A.shape[1])]
res=minimize(obj,np.ones(5)*90,constraints=cons,bounds=bd)
print(res)  #输出解的信息

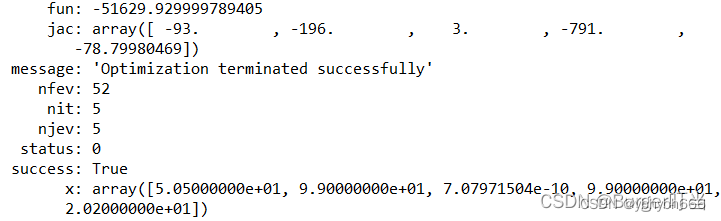
所以，最优解为：x1=50.5,x2=99,x3=0,x4=99,x5=20.2，目标函数的最优值为-51629.93

2. 用cvxopt.solvers模块求解二次规划模型

若非线性规划的目标函数为决策向量x的二次函数，约束条件又全是线性的，就称这种规划为二次规划。

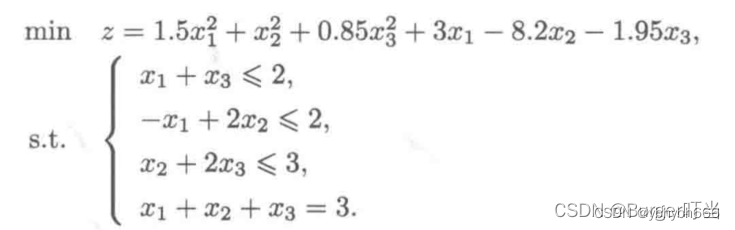
首先将原规划模型化为标准型

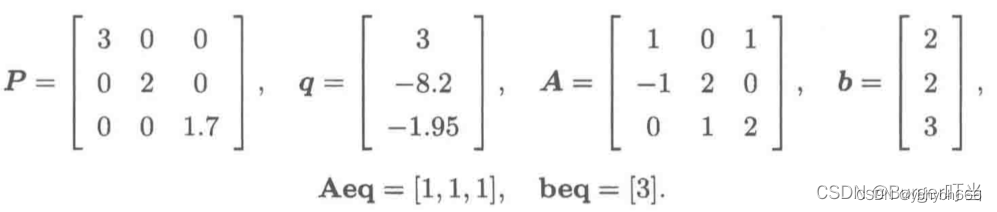
#程序文件Pan6_6.py
import numpy as np
from cvxopt import matrix,solvers
n=3; P=matrix(0.,(n,n))
P[::n+1]=[3,2,1.7]; q=matrix([3,-8.2,-1.95])
A=matrix([[1.,0,1],[-1,2,0],[0,1,2]]).T
b=matrix([2.,2,3])
Aeq=matrix(1.,(1,n)); beq=matrix(3.)
s=solvers.qp(P,q,A,b,Aeq,beq)
print("最优解为：",s['x'])
print("最优值为：",s['primal objective'])

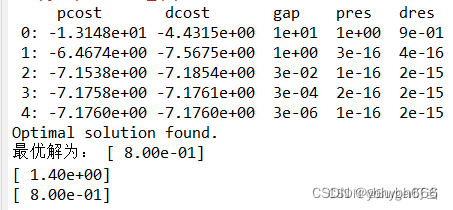
求得最优解为x1=0.8,x2=1.4,x3=0.8,目标函数的最优值为-7.1760