目录
一. 互相关函数
信号y(n)延迟m个时间间隔后与x(n)的互相关函数定义如下:
此定义可以理解为x(n)不动,y(n)左移m个时间单位后与x(n)对应相乘求和的结果。
调换x和y的位置,可得:
理解其几何意义:
:y(n)不动,x(n)左移m个延迟单位与y(n)相乘求和的结果;
:x(n)不动,y(n)右移m个延迟单位后与x(n)相乘求和,此时与
的几何意义是等效的;
关于延迟的图像理解如下:
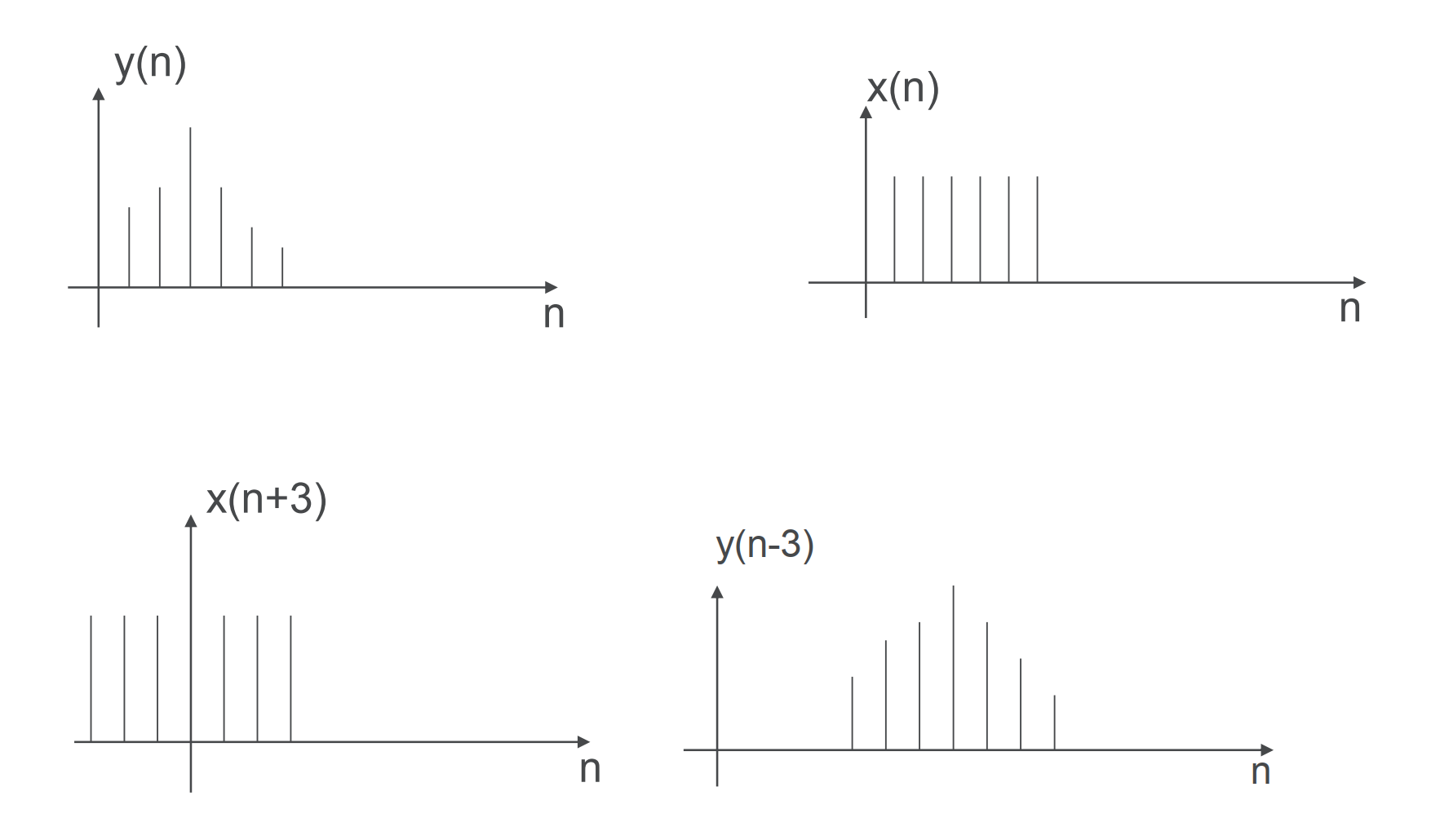
若x(n)和y(n)是复信号,则相关函数定义如下:
上式子中“*”表示取共轭的过程。
如果x(n)与y(n)是功率信号,那么元定义求出的结果趋于无限大,没有物理意义,此时相关函数修改为如下:
二. 自相关函数
若y(n)=x(n),则互相关函数变成了自相关函数,如下:
自相关函数反映了x(n)与自身左移m个时间单位后的信号x(n+m)的相似程度。
若x(n)是功率信号,自相关函数定义为如下:
2.1 自相关函数是一个偶函数
根据定义可得:
令k=n-m,可得:
所以是偶函数,即:
2.2 自相关函数在m=0时,取得最大值
首先易得:
展开平方项,可得:
化简左边形式,可得:
所以可得:
最终可得:
2.3 极限性质
若x(n)是能量信号,则有如下极限性质:
此极限可以理解成,能量有限信号随着时移量逐渐增加,其相关性就逐渐消失,可以从能量有限的角度来理解这个极限。感兴趣的小伙伴可以参考此本书,更加详细:
《信号数字处理的数学原理》 程乾生 石油工业出版社 1979年
2.4 周期信号的自相关函数也是周期的,且与原信号周期相同
假设x(n)的周期为2N+1,所以可得:
由此可得:
三. 互相关函数的性质
不是偶函数,但是满足如下关系:
3.1 函数上界
具有一个上界:
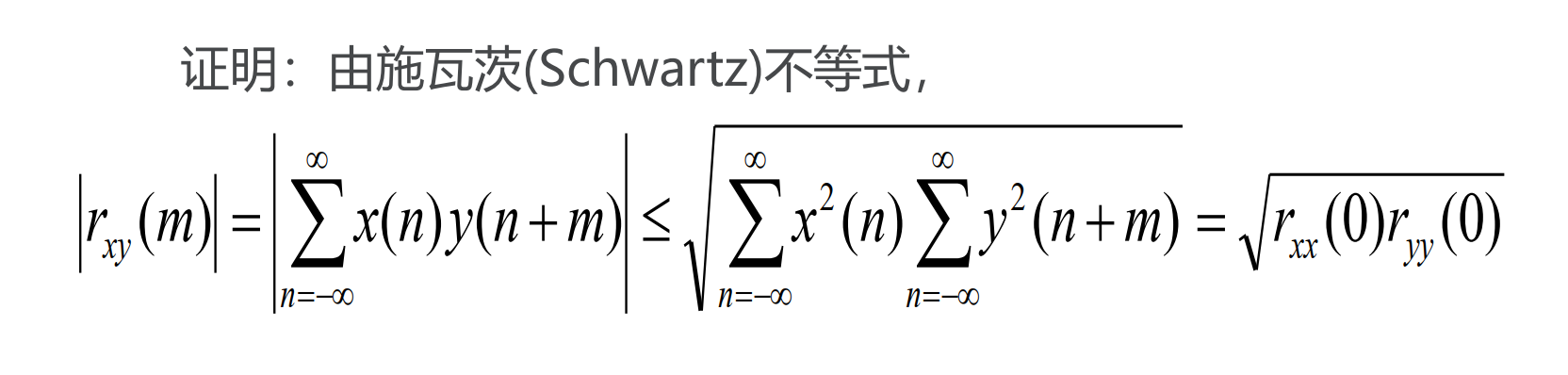
3.2 极限相关
若x(n)和y(n)是能量信号,那么有:
根据定义,只包含了信号x(n)和y(n)的共有频率成分,所以只有当
和
都不为0时,
才不为0。
四. 谱分析
4.1 频谱
假设x(n)为能量信号,则其傅氏Z变换称为x(n)的频谱,如下:
一般而言,上式为复函数,包含幅度谱和相位谱,如下:
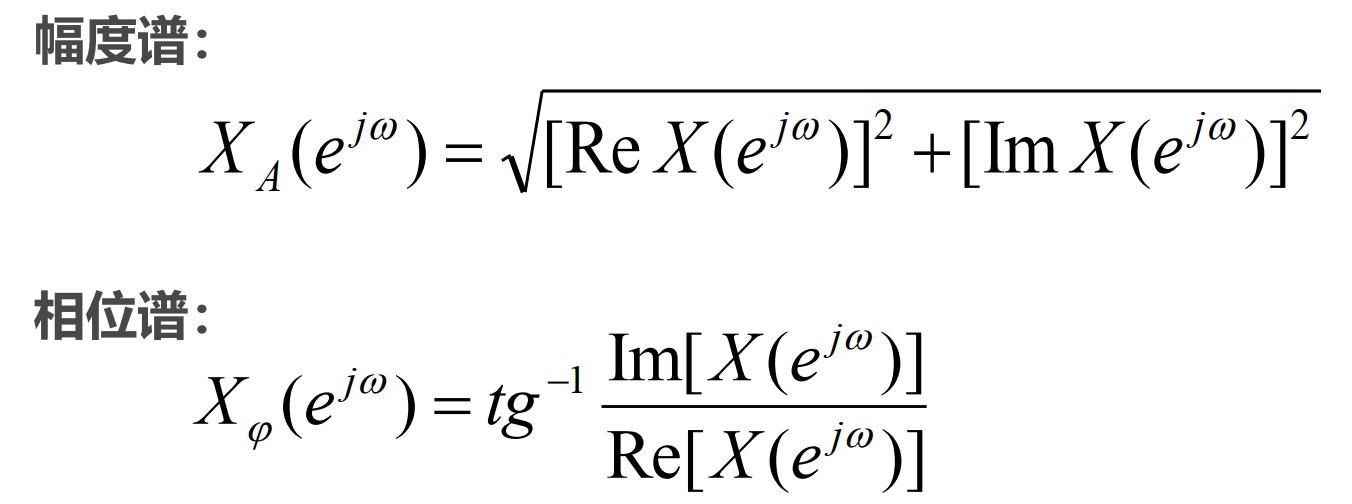
4.2 能量谱
根据帕塞瓦尔定理,有:
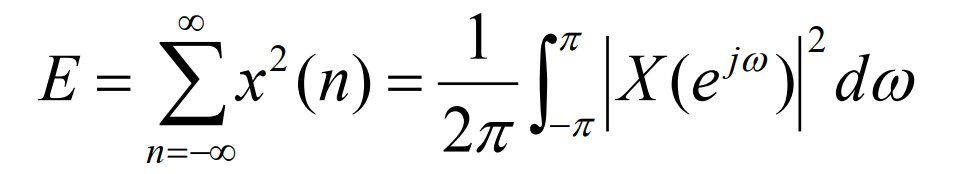
根据自相关函数定义可得:

所以可得:
此反映了信号能量E在频域的分布于,称之为信号的能量密度谱,简称能量谱。
4.3 功率谱
将功率信号x(n)进行截短,形成,如下:
显然是
的能量谱,根据功率信号自相关函数,可得:
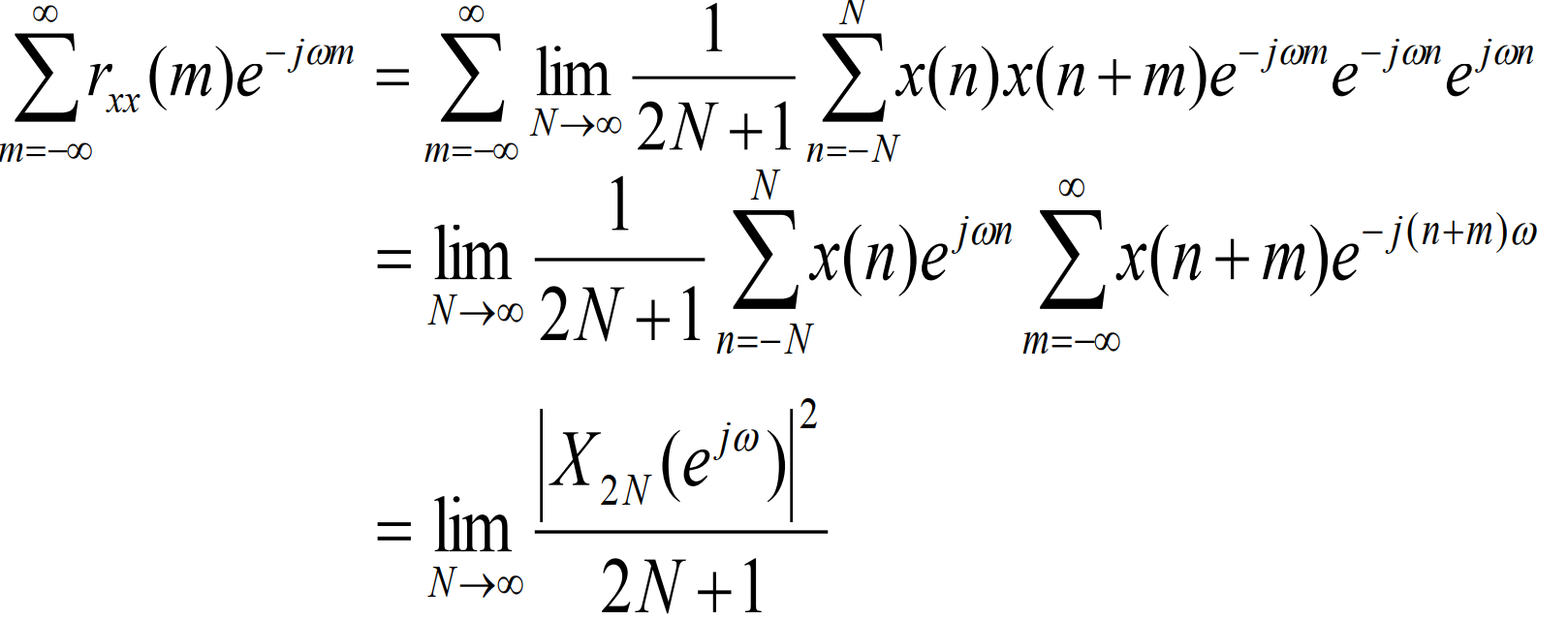
如果该极限可以求出来的话,根据维纳-辛钦定理,则称如下式子为功率密度谱:
功率密度谱也被简称为功率谱。
五. 随机信号的k阶矩
随机信号{x(t)}的k阶矩,定义为:
由此,一阶矩与均值相关:
二阶矩与自相关函数相关:
根据k阶矩是否与时间有关,可以把随机信号分成平稳随机信号和非平稳随机信号。