目录
1.基于RBF网络的滑膜变结构控制系统概述
滑模控制(Sliding Mode Control,SMC)是一种非线性控制策略,用于处理系统参数不确定性、外部干扰和模型误差等问题。近年来,将径向基函数(Radial Basis Function,RBF)网络与滑模控制相结合,形成了基于RBF网络的滑模变结构控制系统,该系统在非线性系统控制中具有良好的性能。本文将详细介绍该控制系统的原理、相关公式以及其优势。由于滑动模态可以进行设计且与对象参数及扰动无关,这就使得变结构控制具有快速响应、对参数变化及扰动不灵敏、无需系统在线辩识, 物理实现简单等优点。该方法的缺点在于当状态轨迹到达滑模面后,难于严格地沿着滑模面向着平衡点滑动,而是在滑模面两侧来回穿越,从而产生颤动,即抖振问题。
基于RBF网络的滑模变结构控制系统的原理: 基于RBF网络的滑模变结构控制系统将滑模控制与RBF神经网络相结合,以增强系统的适应性和鲁棒性。RBF网络是一种前馈神经网络,其基本思想是通过在输入空间中放置一组径向基函数,来近似非线性函数。滑模控制通过引入一个滑模面,将系统的状态引导到滑模面上,以实现对系统的控制。
基于RBF网络的滑模变结构控制系统的主要步骤:
- 系统建模: 首先,对系统进行建模,获得系统的数学表达式和状态空间方程。
- RBF网络设计: 设计RBF网络,选择适当数量的径向基函数以及其参数,用于近似系统的未知非线性部分。
- 滑模面设计: 设计滑模面,通常选择一个超平面,使系统的状态能够在此平面上滑动。
- 控制器设计: 将RBF网络嵌入到滑模控制器中,构建基于RBF网络的滑模变结构控制器。
- 控制律计算: 计算控制律,通过引入滑模面使得系统状态能够在滑模面上滑动,从而实现控制。
- 控制器更新: 基于RBF网络的自适应性,实时更新RBF网络参数,以适应系统的变化和不确定性。
- 系统稳定性分析: 分析系统的稳定性,确保系统在各种工作条件下都能保持稳定。
基于RBF网络的滑模变结构控制系统的优势:
- 适应性: RBF网络能够逼近非线性函数,使控制系统具备较强的适应性,能够处理系统的不确定性和变化。
- 鲁棒性: 滑模控制引入的滑模面能够抵抗外部干扰和模型误差的影响,保证系统稳定性。
- 性能优化: RBF网络能够提高系统的控制性能,使系统的响应更加平滑和快速。
- 非线性处理: 通过RBF网络的逼近能力,基于RBF网络的滑模变结构控制系统能够处理广泛的非线性系统。
基于RBF网络的滑模变结构控制系统在非线性系统控制领域具有重要的应用价值。该系统将滑模控制和RBF网络相融合,实现了对非线性系统的精确控制。通过适应性和鲁棒性的提升,该控制系统在实际工程中表现出色,能够有效应对各种复杂控制问题。
扫描二维码关注公众号,回复:
16395718 查看本文章


2.核心程序
................................................................................
[t,x,u]=ode45('rbf_micishedong',[t0:17:tf],x0);
% [t,x,u]=ode45('micictrl_function',[t0:17:tf],x0);
rol=7400000;
el = 0; %偏心率
Ml = 90*pi/180; %平近点角
nl = sqrt(mu/rol^3);
fal1=sqrt(mu*rol*(1-el^2))*(1+2*el*cos(Ml)+el^2*0.5*(1+5*cos(2*Ml)+el^3))/rol^2;
fal2=2*sqrt(mu*rol*(1-el^2))*(el*nl*sin(Ml)+el^2*(nl*sin(2*Ml)+3*nl*cos(Ml)*sin(Ml))+el^3)/rol^2;
c=diag([0.1;0.1;0.1]);
e=[x(:,7)-x(:,1) x(:,8)-x(:,2) x(:,9)-x(:,3)]';
e1=[x(:,10)-x(:,4) x(:,11)-x(:,5) x(:,12)-x(:,6)]';
s=(e1+c*e)';
E=[e;e1]';
.................................................................................
x0=[zeros(1,3),120];
c1=[-0.5 0 0.5;
-0.5 0 0.5];
b=2;
node=3;
yd=[x(k,7) x(k,8) x(k,9)];
dyd=[x(k,10) x(k,11) x(k,12)];
ddyd=[2*nl*x(k,11)+3*nl^2*x(k,7) -2*nl*x(k,10) -nl^2*x(k,9)];
e=[x(k,7)-x(k,1) x(k,8)-x(k,2) x(k,9)-x(k,3)];
de=[x(k,10)-x(k,4) x(k,11)-x(k,5) x(k,12)-x(k,6)];
kp=0.5;
kd=0.3;
K=[kp kd]';
E=[e;de];
Fai=[0 1;-kp -kd];
A=Fai';
Q=[500 0;0 500];
P=lyap(A,Q);
W=[x(k,10) x(k,11) x(k,12)]';
xi=[e;de];
h=zeros(3,1);
for j=1:1:3
h(j)=exp(-norm(xi(:,j)-c1(:,j))^2/(2*b^2));
end
fxp=W'*h;
fp=[fal1^2*x(k,7)+fal2*x(k,8)+2*fal1*x(k,11)-mu*x(k,7)/((rol+x(k,7))^2+x(k,8)^2+x(k,9)^2)^1.5+mu/rol^2-mu*rol/((rol+x(k,7))^2+x(k,8)^2+x(k,9)^2)^1.5;
-fal2*x(k,7)+fal1^2*x(k,8)-2*fal1*x(k,10)-mu*x(k,8)/((rol+x(k,7))^2+x(k,8)^2+x(k,9)^2)^1.5;
-mu*x(k,9)/((rol+x(k,7))^2+x(k,8)^2+x(k,9)^2)^1.5];
if s==0
tao=diag([0;0;0]);
% lam=0;
else
tao=diag([0.05;0.05;0.05]);
% lam=tao+(f0+abs(D0)*abs(xpd2-fp-c*s))/((eye(3)-D0)*(diag([abs(s(1,1))^beta abs(s(2,1))^beta abs(s(3,1))^beta]))*sign(s));
end
u = inv(b)*(xpd2-fxp*ones(3,1)-c*s-tao*(diag([abs(s(1,1))^beta abs(s(2,1))^beta abs(s(3,1))^beta]))*sign(s));
U(k,:)=u';
end
figure(6);
plot(t,U,'r');
xlabel('time(s)');ylabel('u');
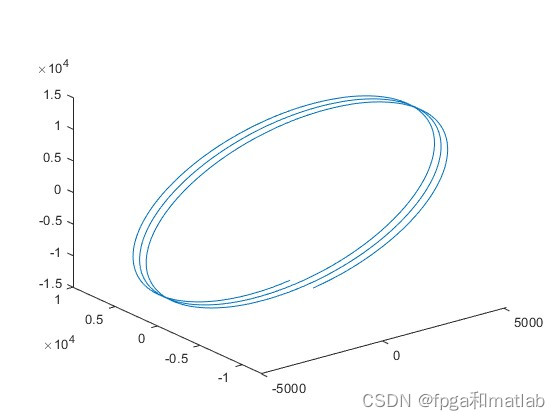
21913.仿真结果