摘要：
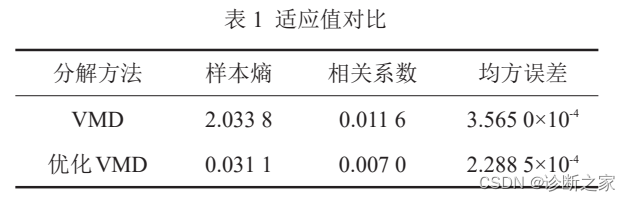
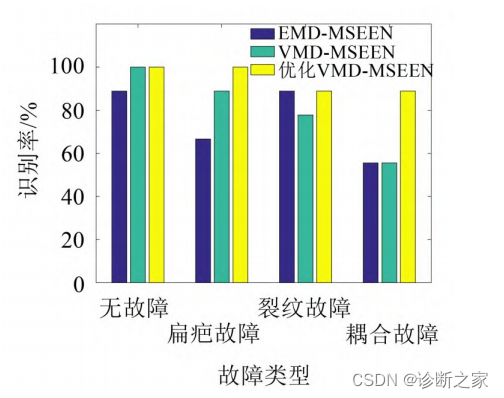
针对列车轮对振动信号易受轮轨噪声影响、故障特征提取困难等问题，提出一种基于优化变分模态分解（Variational mode decomposition，VMD）和多尺度样本熵-能量（Multiscale sample entropy-energy，MSEEN）指标的故障诊断方法。首先搭建考虑轮轨接触关系的轮对振动实验台，分别进行正常、车轮扁疤、车轴裂纹及扁疤-裂纹耦合故障状态下的轮对振动测试。其次，利用遗传算法，以样本熵、相关系数和均方误差为适应值搜索VMD的最佳分解个数及分解中心频率。然后基于优化 VMD 分解不同状态下的轮对振动信号并提取本征模态函数（Intrinsic mode function,IMF）分量的MSEEN指标。最后将指标与BP神经网络结合进行轮对故障诊断，总识别率达到94.44 %。该方法可为实际运行工况中的列车轮对故障诊断提供借鉴。
学习内容：
实际运行工况中的轮对振动信号受到轮轨随机激励、环境噪声等因素影响，具有非线性、非平稳特征，基于传统信号处理方法难以提取故障特征信息。
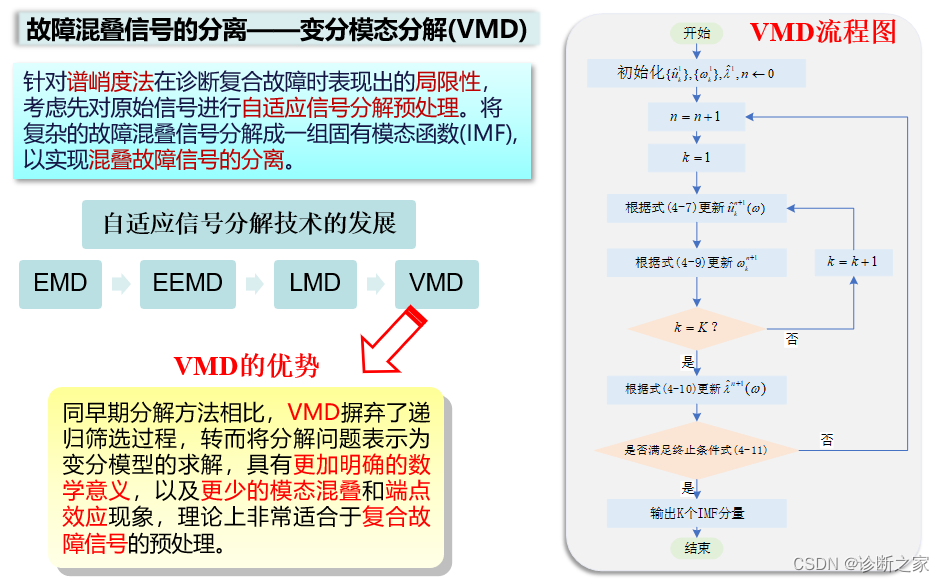
在 经 验 模 态 分 解（Empirical mode decomposition，EMD）的基础上提出的变分模态分解（VMD）可将非平稳信号分解为不同时间尺度的平稳信号，且VMD鲁棒性较强，具有一定的抗噪及抗模态混叠能力。刘秀丽等利用VMD 和小波分析提取了行星轮磨损故障信息。吴东升等使用 VMD 对轴承信号进行降噪，并通过KPCA提取了故障特征信息。孟宗等通过计算 IMF 分量的能量占比确定 VMD 分解个数，提取到轴承的微弱故障特征。焦博隆等使用蝙蝠算法，以样本熵为指标对VMD的分解个数及分解中心频率进行优化，突出了转子裂纹的故障特征。吴守军等利用波形法确定VMD分解个数并对变
速箱故障信号进行了预处理。胡爱军等基于最大相关峭度获得VMD最佳分解中心频率，分离了轴承复合故障。
信息熵可直观反映信号故障状态，常被用来作为设备故障特征指标。吴守军等将散布熵作为变速箱故障特征指标。艾延廷等建立了融合熵距并对转子裂纹-碰摩耦合故障进行了诊断。李伟等基于多尺度模糊熵诊断了齿轮箱故障。潘震等以多尺度排列熵为特征值诊断了单向阀的故障。在样本熵的基础上提出的多尺度样本熵通过对数据进行粗粒化处理，改善了熵值仅在单一尺度上分析的局限性，从而可更准确地反映故障特征。
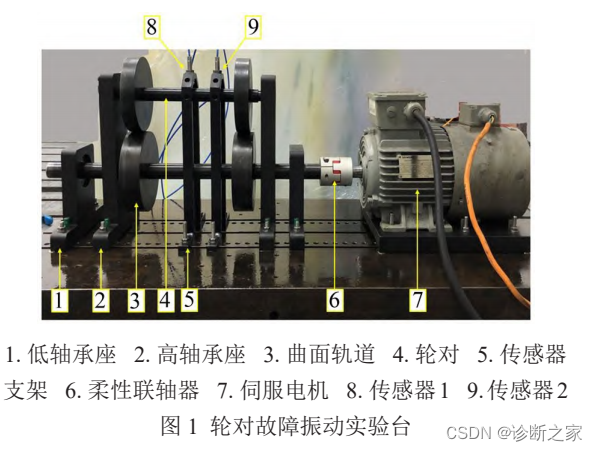
平台照片：
使用该实验台进行轮对系统正常、车轮扁疤、车轴裂纹和耦合故障工况下的振动响应测试。车轴裂纹深度为0.1 d（d为车轴直径），通过线切割获得，车轮扁疤类型为轮面擦伤，如图 2 所示。在建立耦合故障时，两者损伤程度不变。在轮对周围布置两个垂向的电涡流位移传感器。采样频率为 5 000 Hz，采样时间为10 s，轮对转速为600 r/min。
算法原理：
算法优化：
因多尺度样本熵对分布式故障的敏感性较低，故同时引入信号能量（EN）指标，时间序列xi的信号能量EEN的计算公式如下：
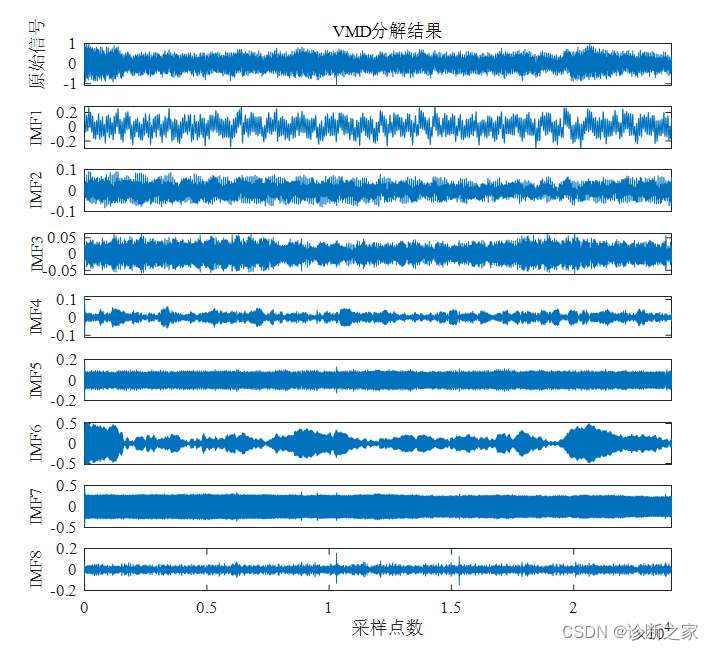
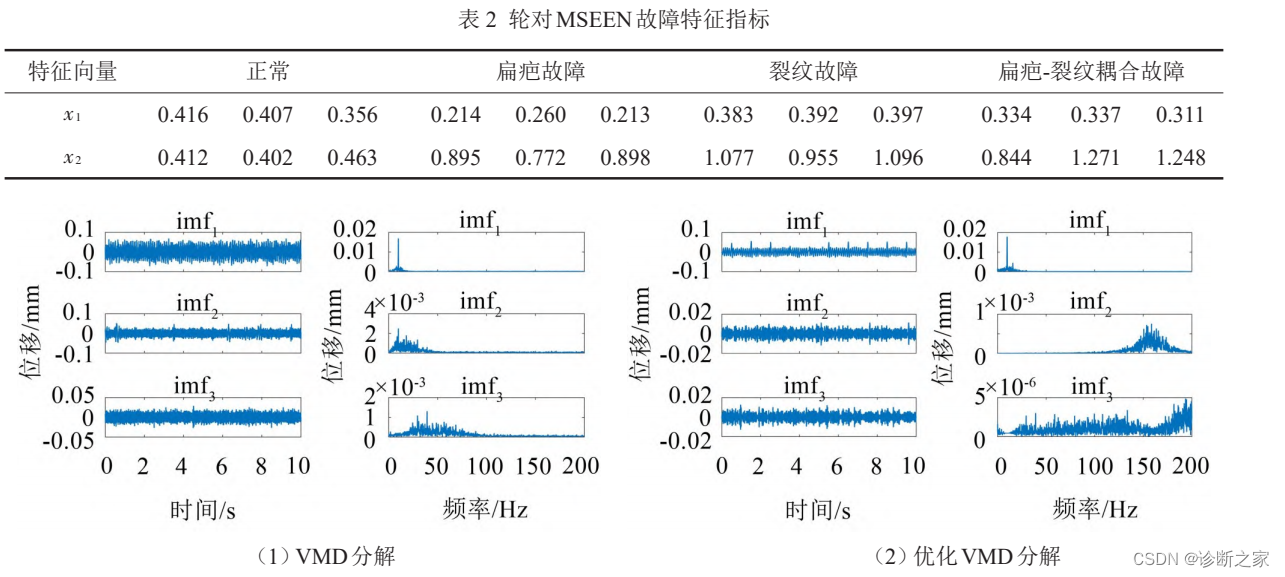
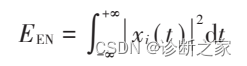构建多尺度样本熵-能量指标XMSEEN作为轮对故障诊断特征向量，XMSEEN = { x1、x2}，x1，x2分别为IMF1分量的多尺度样本熵HMSE和信号能量EEN。
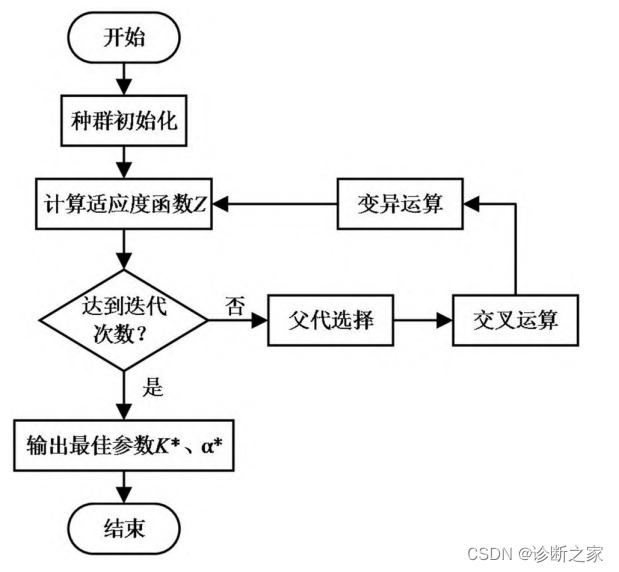
最终结果：
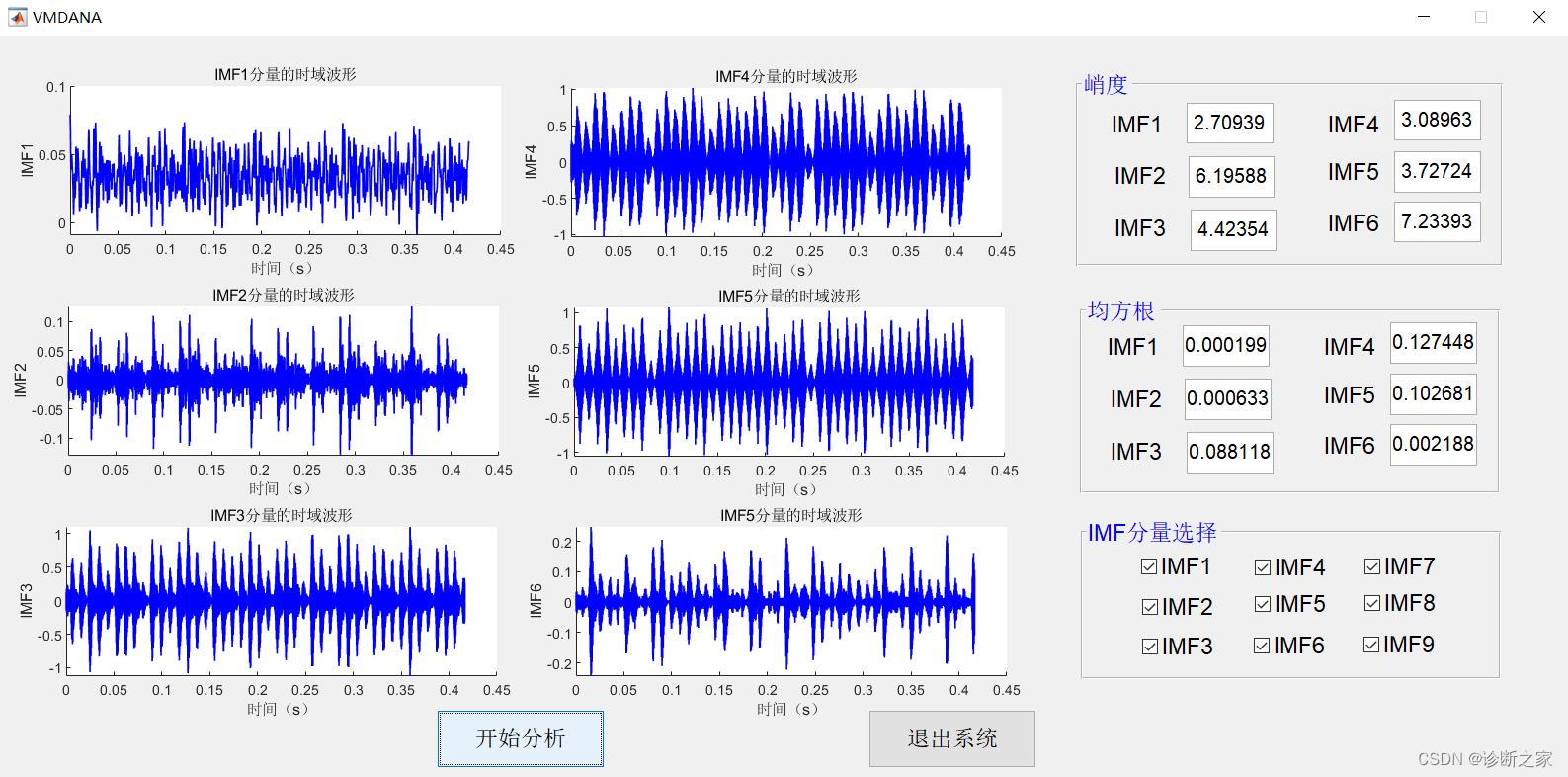
程序代码：
Vxin: forwardtszs 扣扣：571485322
公众号：滚动轴承故障诊断与寿命预测
# -*- coding: utf-8 -*-
"""
Created on Wed Feb 20 19:24:58 2019
@author: Vinícius Rezende Carvalho
"""
import numpy as np
def VMD(f, alpha, tau, K, DC, init, tol):
"""
u,u_hat,omega = VMD(f, alpha, tau, K, DC, init, tol)
Variational mode decomposition
Python implementation by Vinícius Rezende Carvalho - vrcarva@gmail.com
code based on Dominique Zosso's MATLAB code, available at:
https://www.mathworks.com/matlabcentral/fileexchange/44765-variational-mode-decomposition
Original paper:
Dragomiretskiy, K. and Zosso, D. (2014) ‘Variational Mode Decomposition’,
IEEE Transactions on Signal Processing, 62(3), pp. 531–544. doi: 10.1109/TSP.2013.2288675.
Input and Parameters:
---------------------
f - the time domain signal (1D) to be decomposed
alpha - the balancing parameter of the data-fidelity constraint
tau - time-step of the dual ascent ( pick 0 for noise-slack )
K - the number of modes to be recovered
DC - true if the first mode is put and kept at DC (0-freq)
init - 0 = all omegas start at 0
1 = all omegas start uniformly distributed
2 = all omegas initialized randomly
tol - tolerance of convergence criterion; typically around 1e-6
Output:
-------
u - the collection of decomposed modes
u_hat - spectra of the modes
omega - estimated mode center-frequencies
"""
if len(f)%2:
f = f[:-1]
# Period and sampling frequency of input signal
fs = 1./len(f)
ltemp = len(f)//2
fMirr = np.append(np.flip(f[:ltemp],axis = 0),f)
fMirr = np.append(fMirr,np.flip(f[-ltemp:],axis = 0))
# Time Domain 0 to T (of mirrored signal)
T = len(fMirr)
t = np.arange(1,T+1)/T
# Spectral Domain discretization
freqs = t-0.5-(1/T)
# Maximum number of iterations (if not converged yet, then it won't anyway)
Niter = 500
# For future generalizations: individual alpha for each mode
Alpha = alpha*np.ones(K)
# Construct and center f_hat
f_hat = np.fft.fftshift((np.fft.fft(fMirr)))
f_hat_plus = np.copy(f_hat) #copy f_hat
f_hat_plus[:T//2] = 0
# Initialization of omega_k
omega_plus = np.zeros([Niter, K])
if init == 1:
for i in range(K):
omega_plus[0,i] = (0.5/K)*(i)
elif init == 2:
omega_plus[0,:] = np.sort(np.exp(np.log(fs) + (np.log(0.5)-np.log(fs))*np.random.rand(1,K)))
else:
omega_plus[0,:] = 0
# if DC mode imposed, set its omega to 0
if DC:
omega_plus[0,0] = 0
# start with empty dual variables
lambda_hat = np.zeros([Niter, len(freqs)], dtype = complex)
# other inits
uDiff = tol+np.spacing(1) # update step
n = 0 # loop counter
sum_uk = 0 # accumulator
# matrix keeping track of every iterant // could be discarded for mem
u_hat_plus = np.zeros([Niter, len(freqs), K],dtype=complex)
#*** Main loop for iterative updates***
while ( uDiff > tol and n < Niter-1 ): # not converged and below iterations limit
# update first mode accumulator
k = 0
sum_uk = u_hat_plus[n,:,K-1] + sum_uk - u_hat_plus[n,:,0]
# update spectrum of first mode through Wiener filter of residuals
u_hat_plus[n+1,:,k] = (f_hat_plus - sum_uk - lambda_hat[n,:]/2)/(1.+Alpha[k]*(freqs - omega_plus[n,k])**2)
# update first omega if not held at 0
if not(DC):
omega_plus[n+1,k] = np.dot(freqs[T//2:T],(abs(u_hat_plus[n+1, T//2:T, k])**2))/np.sum(abs(u_hat_plus[n+1,T//2:T,k])**2)
# update of any other mode
for k in np.arange(1,K):
#accumulator
sum_uk = u_hat_plus[n+1,:,k-1] + sum_uk - u_hat_plus[n,:,k]
# mode spectrum
u_hat_plus[n+1,:,k] = (f_hat_plus - sum_uk - lambda_hat[n,:]/2)/(1+Alpha[k]*(freqs - omega_plus[n,k])**2)
# center frequencies
omega_plus[n+1,k] = np.dot(freqs[T//2:T],(abs(u_hat_plus[n+1, T//2:T, k])**2))/np.sum(abs(u_hat_plus[n+1,T//2:T,k])**2)
# Dual ascent
lambda_hat[n+1,:] = lambda_hat[n,:] + tau*(np.sum(u_hat_plus[n+1,:,:],axis = 1) - f_hat_plus)
# loop counter
n = n+1
# converged yet?
uDiff = np.spacing(1)
for i in range(K):
uDiff = uDiff + (1/T)*np.dot((u_hat_plus[n,:,i]-u_hat_plus[n-1,:,i]),np.conj((u_hat_plus[n,:,i]-u_hat_plus[n-1,:,i])))
uDiff = np.abs(uDiff)
#Postprocessing and cleanup
#discard empty space if converged early
Niter = np.min([Niter,n])
omega = omega_plus[:Niter,:]
idxs = np.flip(np.arange(1,T//2+1),axis = 0)
# Signal reconstruction
u_hat = np.zeros([T, K],dtype = complex)
u_hat[T//2:T,:] = u_hat_plus[Niter-1,T//2:T,:]
u_hat[idxs,:] = np.conj(u_hat_plus[Niter-1,T//2:T,:])
u_hat[0,:] = np.conj(u_hat[-1,:])
u = np.zeros([K,len(t)])
for k in range(K):
u[k,:] = np.real(np.fft.ifft(np.fft.ifftshift(u_hat[:,k])))
# remove mirror part
u = u[:,T//4:3*T//4]
# recompute spectrum
u_hat = np.zeros([u.shape[1],K],dtype = complex)
for k in range(K):
u_hat[:,k]=np.fft.fftshift(np.fft.fft(u[k,:]))
return u, u_hat, omega