目录
一.堆的逻辑结构与物理结构
堆满足两个条件:
1.堆中的某个节点的值总是不大于或不小于其父节点的值
2.堆总是一颗完全二叉树
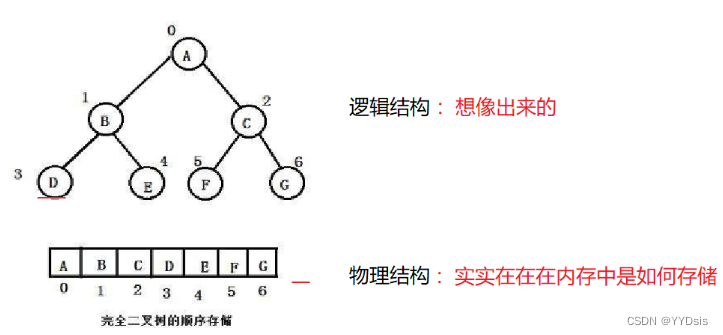
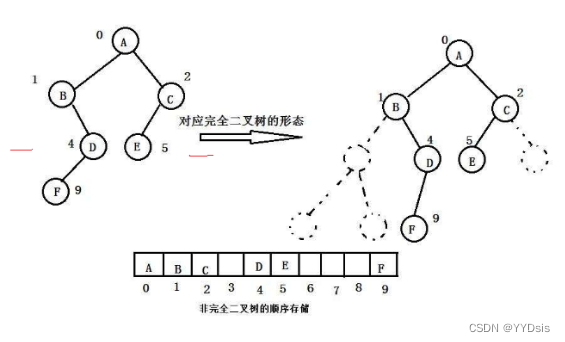
1.数组存储方式表示二叉树
数组存储表示二叉树只适合完全二叉树,以为会浪费很多空间
2.堆中的父子关系
3.大小堆的基本概念
大根堆:树中父亲结点都大于/等于孩子
小根堆:树种父亲结点都小于/等于孩子
二.堆的两种调整方式
PS:已有堆的基础上,对下标(parent,child)对应的元素进行调整
1.向上调整(时间复杂度O(nlogn))
【参数:数组,孩子】
// 除了child这个位置,前面数据构成堆 void AdjustUp(HPDataType* a, int child) { int parent = (child - 1) / 2; //while (parent >= 0) while(child > 0) { if (a[child] > a[parent]) { Swap(&a[child], &a[parent]); child = parent; parent = (child - 1) / 2; } else { break; } } }
2.向下调整(时间复杂度O(n))
注意:向下调整有个条件,左右子树都必须是大堆/小堆
【为满足此条件:如要建堆,要从底部第一个父母结点开始调整,代码体现如下】
【参数:数组,界限,父母】
代码体现:
// 左右子树都是大堆/小堆
void AdjustDown(HPDataType* a, int n, int parent)
{
int child = parent * 2 + 1;
while (child < n)
{
// 选出左右孩子中大的那一个
if (child + 1 < n && a[child+1] > a[child])
{
++child;
}
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}三.建堆
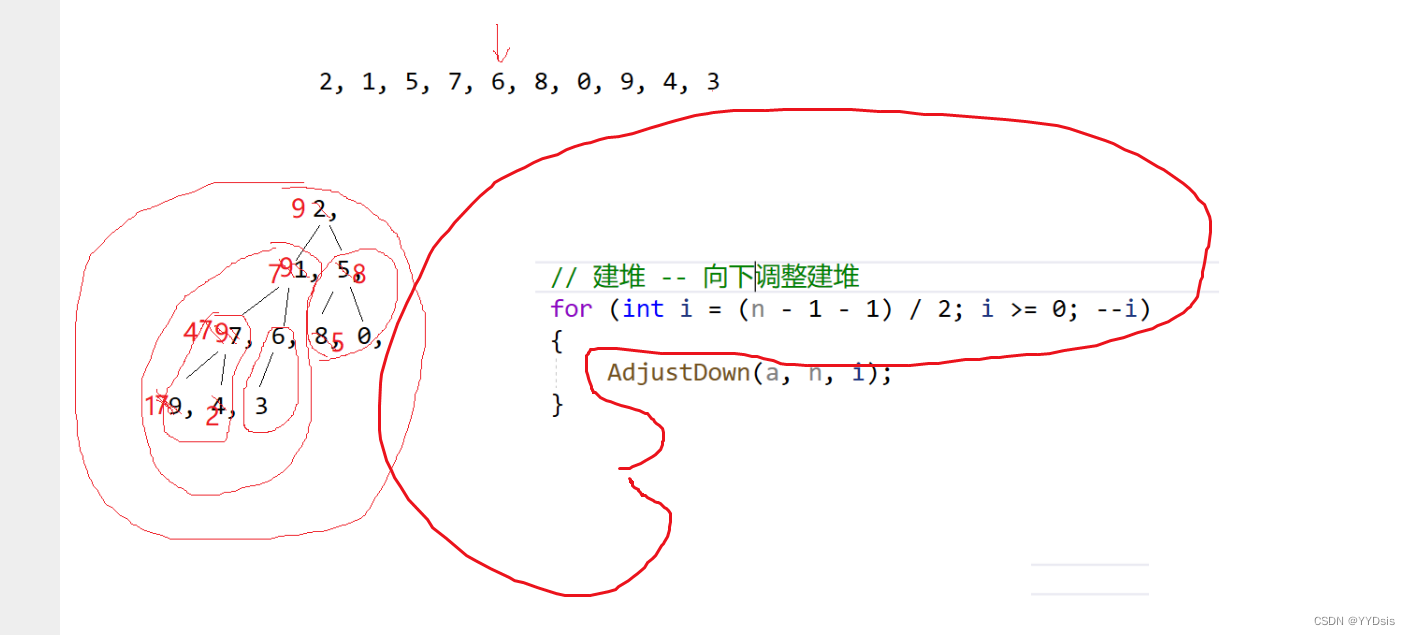
1.向下调整建堆法
向下调整建堆必须要满足左右子树都是大/小堆。
故建堆要从倒数第一个父母结点开始往回遍历建堆。
void HeapSort(int* a, int n) { // 建堆 -- 向下调整建堆 for (int i = ((n-1)-1)/2; i < n; ++i) //((n-1)-1)/2是第一个父母结点 { AdjustUp(a, i); } // 自己先实现 }
2.向上调整建堆
直接遍历。
void HeapSort(int* a, int n) { // 建堆 -- 向上调整建堆 for (int i = 1; i < n; ++i) { AdjustUp(a, i); } // 自己先实现 }
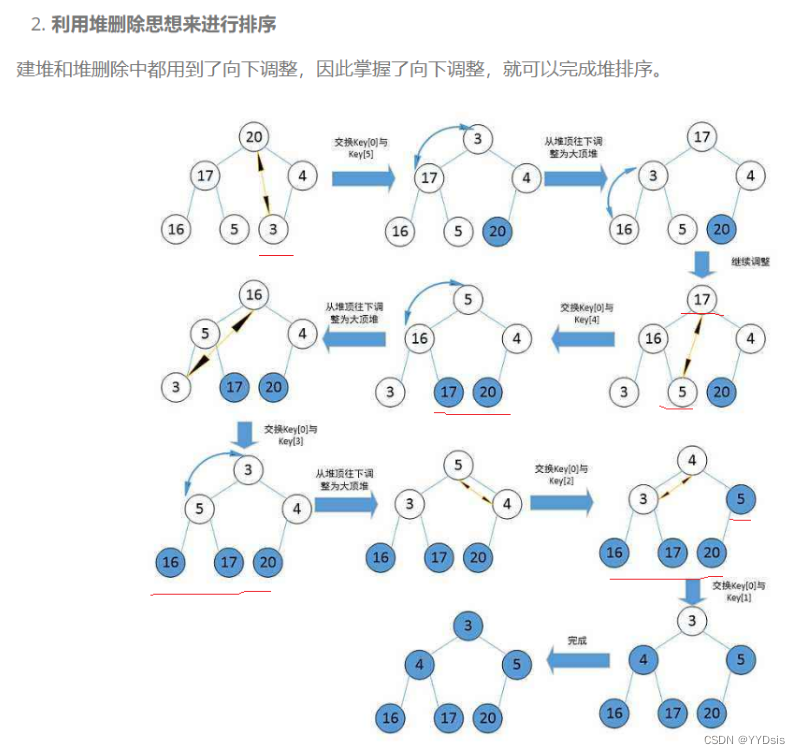
四.堆排序(利用堆删除的思想来进行排序)
1.排升序——建大堆
分析:
1.可以确保每次替换后,最大的数都会到数结尾。
2.可以确保每次替换后,再对除最末结点以外的树进行调整,剩下中最大的数会到祖先节点。
// 排升序 -- 建大堆 -- O(N*logN) void HeapSort(int* a, int n) { // 建堆 -- 向上调整建堆 -- O(N*logN) /*for (int i = 1; i < n; ++i) { AdjustUp(a, i); }*/ // 建堆 -- 向下调整建堆 -- O(N) for (int i = (n - 1 - 1) / 2; i >= 0; --i) { AdjustDown(a, n, i); } // 自己先实现 -- O(N*logN) int end = n - 1; while (end > 0) { Swap(&a[end], &a[0]); AdjustDown(a, end, 0); --end; } }
2.排降序——建小堆
(与上同理 )
3.堆排序复杂度分析
1.由数学计算:向上调整时间复杂度为O(nlogn),向下调整时间复杂度为O(n)
2.由二叉树数学关系,大致得出从祖先结点到最后一层排序的耗费大约为2^(h-1)*(h-1),
知其耗费的个数约为总数的一半。由时间复杂度可忽略有理数可得时间复杂度O(nlogn)
可见博主相关二叉树博客:(62条消息) (二叉)树的基础入门(简洁易懂,含代码)_YYDsis的博客-CSDN博客

五.实际应用(top-k问题)
void CreateNDate() { // 造数据 int n = 10000000; srand(time(0)); const char* file = "data.txt"; FILE* fin = fopen(file, "w"); if (fin == NULL) { perror("fopen error"); return; } for (size_t i = 0; i < n; ++i) { int x = rand() % 10000; fprintf(fin, "%d\n", x); } fclose(fin); } void PrintTopK(const char* file, int k) { // 1. 建堆--用a中前k个元素建小堆 int* topk = (int*)malloc(sizeof(int) * k); assert(topk); FILE* fout = fopen(file, "r"); if (fout == NULL) { perror("fopen error"); return; } // 读出前k个数据建小堆 for(int i = 0; i < k; ++i) { fscanf(fout, "%d", &topk[i]); } for (int i = (k-2)/2; i >= 0; --i) { AdjustDown(topk, k, i); } // 2. 将剩余n-k个元素依次与堆顶元素交换,不满则则替换 int val = 0; int ret = fscanf(fout, "%d", &val);//自动跳到下一个 while (ret != EOF) { if (val > topk[0]) { topk[0] = val; AdjustDown(topk, k, 0); } ret = fscanf(fout, "%d", &val); } for (int i = 0; i < k; i++) { printf("%d ", topk[i]); } printf("\n"); free(topk); fclose(fout); }