title: （左倾）红黑树推演总结
date: 2023-06-01 09:09:12
tags:

数据结构
算法
categories:
数据结构与算法
cover: https://cover.png
feature: false

前置知识：树、二叉树与二叉查找树，见 Fan’s Web 树的部分

1. 2-3 查找树

为了保证查找树的平衡性，我们需要一些灵活性，因此在这里我们允许树中的一个结点保存多个键。确切地说，我们将一棵标准的二叉查找树中的结点称为 2- 结点（含有一个键和两条链接），而现在我们引入 3- 结点，它含有两个键和三条链接。2- 结点和 3- 结点中的每条链接都对应着其中保存的键所分割产生的一个区间

一棵 2-3 查找树或为一棵空树，或由以下结点组成：

2- 结点，含有一个键（及其对应的值）和两条链接，左链接指向的 2-3 树中的键都小于该结点，右链接指向的 2-3 树中的键都大于该结点

3- 结点，含有两个键（及其对应的值）和三条链接，左链接指向的 2-3 树中的键都小于该结点，中链接指向的 2-3 树中的键都位于该结点的两个键之间，右链接指向的 2-3 树中的键都大于该结点

我们将指向一棵空树的链接称为空链接

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JHAzoTir-1689581422523)(http://img.fan223.cn/2023/05/20230531110715.png)]

一棵完美平衡的 2-3 查找树中的所有空链接到根结点的距离都应该是相同的

1.1 查找

将二叉查找树的查找算法一般化我们就能够直接得到 2-3 树的查找算法。要判断一个键是否在树中，我们先将它和根结点中的键比较。如果它和其中任意一个相等，查找命中；否则我们就根据比较的结果找到指向相应区间的链接，并在其指向的子树中递归地继续查找。如果这是个空链接，查找未命中

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-knMI5okl-1689581422524)(http://img.fan223.cn/2023/05/20230531110930.png)]

1.2 向 2- 结点中插入新键

要在 2-3 树中插入一个新结点，我们可以和二叉查找树一样先进行一次未命中的查找，然后把新结点挂在树的底部。但这样的话树无法保持完美平衡性。我们使用 2-3 树的主要原因就在于它能够在插入后继续保持平衡。如果未命中的查找结束于一个 2- 结点，事情就好办了：我们只要把这个 2- 结点替换为一个 3- 结点，将要插入的键保存在其中即可

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-V1Tq1yFL-1689581539422)(https://img.fan223.cn/2023/05/20230531111107.png)]

扫描二维码关注公众号，回复： 15797951 查看本文章

1.3 向一棵只含有一个 3- 结点的树中插入新键

如果未命中的查找结束于一个 3- 结点，事情就要麻烦一些

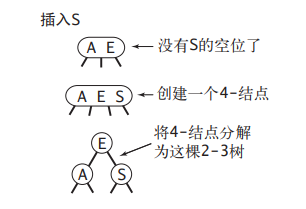
在考虑一般情况之前，先假设我们需要向一棵只含有一个 3- 结点的树中插入一个新键。这棵树中有两个键，所以在它唯一的结点中已经没有可插入新键的空间了。为了将新键插入，我们先临时将新键存入该结点中，使之成为一个 4- 结点

它很自然地扩展了以前的结点并含有 3 个键和 4 条链接。创建一个 4- 结点很方便，因为很容易将它转换为一棵由 3 个 2- 结点组成的 2-3 树，其中一个结点（根）含有中键，一个结点含有 3 个键中的最小者（和根结点的左链接相连），一个结点含有 3 个键中的最大者（和根结点的右链接相连）。这棵树既是一棵含有 3 个结点的二叉查找树，同时也是一棵完美平衡的 2-3 树，因为其中所有的空链接到根结点的距离都相等。插入前树的高度为 0，插入后树的高度为 1

1.4 向一个父结点为 2- 结点的 3- 结点中插入新键

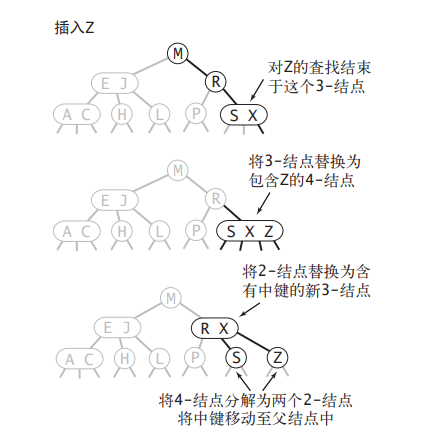
假设未命中的查找结束于一个 3- 结点，而它的父结点是一个 2- 结点。在这种情况下我们需要在维持树的完美平衡的前提下为新键腾出空间

先像上面一样构造一个临时的 4- 结点并将其分解，但此时我们不会为中键创建一个新结点，而是将其移动至原来的父结点中。可以将这次转换看成将指向原 3- 结点的一条链接替换为新父结点中的原中键左右两边的两条链接，并分别指向两个新的 2- 结点

根据我们的假设，父结点中是有空间的：父结点是一个 2- 结点（一个键两条链接），插入之后变为了一个 3- 结点（两个键 3 条链接）。另外，这次转换也并不影响（完美平衡的）2-3 树的主要性质。树仍然是有序的，因为中键被移动到父结点中去了；树仍然是完美平衡的，插入后所有的空链接到根结点的距离仍然相同

1.5 向一个父结点为 3- 结点的 3- 结点中插入新键

现在假设未命中的查找结束于一个父结点为 3- 结点的结点。我们再次和前面一样构造一个临时的 4- 结点并分解它，然后将它的中键插入它的父结点中。但父结点也是一个 3- 结点，因此我们再用这个中键构造一个新的临时 4- 结点，然后在这个结点上进行相同的变换，即分解这个父结点并将它的中键插入到它的父结点中去

推广到一般情况，我们就这样一直向上不断分解临时的 4- 结点并将中键插入更高层的父结点，直至遇到一个 2- 结点并将它替换为一个不需要继续分解的 3- 结点，或者是到达 3- 结点的根

1.6 分解根结点

如果从插入结点到根结点的路径上全都是 3- 结点，我们的根结点最终变成一个临时的 4- 结点。此时我们可以按照向一棵只有一个 3- 结点的树中插入新键的方法处理这个问题。我们将临时的 4- 结点分解为 3 个 2- 结点，使得树高加 1。注意，这次最后的变换仍然保持了树的完美平衡性，因为它变换的是根结点

1.7 局部变换

将一个 4- 结点分解为一棵 2-3 树可能有 6 种情况

这个 4- 结点可能是根结点
可能是一个 2- 结点的左子结点
可能是一个 2- 结点的右子结点
也可能是一个 3- 结点的左子结点
也可能是一个 3- 结点的中子结点
也可能是一个 3- 结点的右子结点

2-3 树插入算法的根本在于这些变换都是局部的：除了相关的结点和链接之外不必修改或者检查树的其他部分。每次变换中，变更的链接数量不会超过一个很小的常数。需要特别指出的是，不光是在树的底部，树中的任何地方只要符合相应的模式，变换都可以进行。每个变换都会将 4- 结点中的一个键送入它的父结点中，并重构相应的链接而不必涉及树的其他部分

1.8 全局性质

这些局部变换不会影响树的全局有序性和平衡性：任意空链接到根结点的路径长度都是相等的。下图所示的是当一个 4- 结点是一个 3- 结点的中子结点时的完整变换情况

如果在变换之前根结点到所有空链接的路径长度为 h，那么变换之后该长度仍然为 h。所有的变换都具有这个性质，即使是将一个 4- 结点分解为两个 2- 结点并将其父结点由 2- 结点变为 3- 结点，或是由 3- 结点变为一个临时的 4- 结点时也是如此

当根结点被分解为 3 个 2- 结点时，所有空链接到根结点的路径长度才会加 1

1.9 分析与小结

和标准的二叉查找树由上向下生长不同，2-3 树的生长是由下向上的。下图是标准索引测试用例中产生的一系列 2-3 树，以及一系列由同一组键按照升序依次插入到树中时所产生的所有 2-3 树

在二叉查找树中，按照升序插入 10 个键会得到高度为 9 的一棵最差查找树。如果使用 2-3 树，树的高度是 2

在一棵大小为 N 的 2-3 树中，查找和插入操作访问的结点必然不超过 lgN 个

一棵含有 N 个结点的 2-3 树的高度在 ⌊log3N⌋=⌊(lgN)/(lg3)⌋（如果树中全是 3- 结点）和 ⌊lgN⌋（如果树中全是 2-结点）之间

因此我们可以确定 2-3 树在最坏情况下仍有较好的性能。每个操作中处理每个结点的时间都不会超过一个很小的常数，且这两个操作都只会访问一条路径上的结点，所以任何查找或者插入的成本都肯定不会超过对数级别

对比由相同的键构造的 2-3 树和二叉查找树，完美平衡的 2-3 树要平展得多。例如，含有 10 亿个结点的一棵 2-3 树的高度仅在 19 到 30 之间。我们最多只需要访问 30 个结点就能够在 10 亿个键中进行任意查找和插入操作，这是相当惊人的

但是，我们和真正的实现还有一段距离。尽管我们可以用不同的数据类型表示2-结点和3-结点并写出变换所需的代码，但用这种直白的表示方法实现大多数的操作并不方便，因为需要处理的情况实在太多

我们需要维护两种不同类型的结点，将被查找的键和结点中的每个键进行比较，将链接和其他信息从一种结点复制到另一种结点，将结点从一种数据类型转换到另一种数据类型，等等。实现这些不仅需要大量的代码，而且它们所产生的额外开销可能会使算法比标准的二叉查找树更慢。平衡一棵树的初衷是为了消除最坏情况，但我们希望这种保障所需的代码能够越少越好

2 红黑二叉查找树（红黑树）

前面所述的 2-3 树的插入算法并不难理解，同时它也不难实现。我们要用一种名为红黑二叉查找树的简单数据结构来表达并实现它，最后的代码量并不大

2.1 替换 3- 结点

红黑二叉查找树背后的基本思想是用标准的二叉查找树（完全由 2- 结点构成）和一些额外的信息（替换 3- 结点）来表示 2-3 树

我们将树中的链接分为两种类型：红链接将两个 2- 结点连接起来构成一个 3- 结点，黑链接则是 2-3 树中的普通链接。确切地说，我们将 3- 结点表示为由一条左斜的红色链接（两个 2- 结点其中之一是另一个的左子结点）相连的两个 2- 结点

这种表示法的一个优点是，我们无需修改就可以直接使用标准二叉查找树的 get() 方法。对于任意的 2-3 树，只要对结点进行转换，我们都可以立即派生出一棵对应的二叉查找树。我们将用这种方式表示 2-3 树的二叉查找树称为红黑二叉查找树（以下简称为红黑树）

2.2 等价定义

红黑树的另一种定义是含有红黑链接并满足下列条件的二叉查找树：

红链接均为左链接
没有任何一个结点同时和两条红链接相连
该树是完美黑色平衡的，即任意空链接到根结点的路径上的黑链接数量相同

满足这样定义的红黑树和相应的 2-3 树是一一对应的

如果我们将一棵红黑树中的红链接画平，那么所有的空链接到根结点的距离都将是相同的

如果我们将由红链接相连的结点合并，得到的就是一棵 2-3 树。相反，如果将一棵 2-3 树中的 3- 结点画作由红色左链接相连的两个 2- 结点，那么不会存在能够和两条红链接相连的结点，且树必然是完美黑色平衡的，因为黑链接即 2-3 树中的普通链接，根据定义这些链接必然是完美平衡的。无论我们选择用何种方式去定义它们，红黑树都既是二叉查找树，也是 2-3 树

因此，如果我们能够在保持一一对应关系的基础上实现 2-3 树的插入算法，那么我们就能够将两个算法的优点结合起来：二叉查找树中简洁高效的查找方法和 2-3 树中高效的平衡插入算法

2.3 颜色表示

方便起见，因为每个结点都只会有一条指向自己的链接（从它的父结点指向它），我们将链接的颜色保存在表示结点的 Node 数据类型的布尔变量 color 中。如果指向它的链接是红色的，那么该变量为 true，黑色则为false

我们约定空链接为黑色。为了代码的清晰，我们定义了两个常量 RED 和 BLACK 来设置和测试这个变量。我们使用私有方法 isRed() 来测试一个结点和它的父结点之间的链接的颜色。当我们提到一个结点的颜色时，我们指的是指向该结点的链接的颜色，反之亦然

2.4 旋转

在我们实现的某些操作中可能会出现红色右链接或者两条连续的红链接，但在操作完成前这些情况都会被小心地旋转并修复。旋转操作会改变红链接的指向

首先，假设我们有一条红色的右链接需要被转化为左链接（左旋转 h 的右链接，h 表示 E 结点，x 表示 S 结点）

这个操作叫做左旋转，它对应的方法接受一条指向红黑树中的某个结点的链接作为参数。假设被指向的结点的右链接是红色的，这个方法会对树进行必要的调整并返回一个指向包含同一组键的子树且其左链接为红色的根结点的链接。这个操作很容易理解：我们只是将用两个键中的较小者作为根结点变为将较大者作为根结点

实现将一个红色左链接转换为一个红色右链接的一个右旋转的代码完全相同，只需要将 left 和 right 互换即可（右旋转 h 的左链接，h 表示 S 结点，x 表示 E 结点）

2.5 在旋转后重置父结点的链接

无论左旋转还是右旋转，旋转操作都会返回一条链接，我们总是会用 rotateRight() 或 rotateLeft() 的返回值重置父结点（或是根结点)中相应的链接

返回的链接可能是左链接也可能是右链接，但是我们总会将它赋予父结点中的链接
这个链接可能是红色也可能是黑色——rotateLeft() 和 rotateRight() 都通过将 x.color 设为 h.color 保留它原来的颜色
这可能会产生两条连续的红链接，但我们的算法会继续用旋转操作修正这种情况。例如，代码 h = rotateLeft(h); 将旋转结点 h 的红色右链接，使得 h 指向了旋转后的子树的根结点（组成该子树中的所有键和旋转前相同，只是根结点发生了变化)

这种简洁的代码是我们使用递归实现二叉查找树的各种方法的主要原因，它使得旋转操作成为了普通插入操作的一个简单补充

在插入新的键时我们可以使用旋转操作帮助我们保证 2-3 树和红黑树之间的一一对应关系，因为旋转操作可以保持红黑树的两个重要性质：有序性和完美平衡性。也就是说，我们在红黑树中进行旋转时无需为树的有序性或者完美平衡性担心。下面我们来看看应该如何使用旋转操作来保持红黑树的另外两个重要性质（不存在两条连续的红链接和不存在红色的右链接）

2.6 向单个 2- 结点中插入新键

一棵只含有一个键的红黑树只含有一个 2- 结点，插入另一个键之后，我们马上就需要将它们旋转

如果新键小于老键，我们只需要新增一个红色的结点即可，新的红黑树和单个 3- 结点完全等价
如果新键大于老键，那么新增的红色结点将会产生一条红色的右链接。我们需要使用 root = rotateLeft(root); 来将其旋转为红色左链接并修正根结点的链接，插入操作才算完成

两种情况的结果均为一棵和单个 3- 结点等价的红黑树，其中含有两个键，一条红链接，树的黑链接高度为 1

2.7 向树底部的 2- 结点插入新键

用和二叉查找树相同的方式向一棵红黑树中插人一个新键会在树的底部新增一个结点（为了保证有序性），但总是用红链接将新结点和它的父结点相连

如果它的父结点是一个 2- 结点，那么上面的两种处理方法仍然适用
如果指向新结点的是父结点的左链接，那么父结点就直接成为了一个 3- 结点
如果指向新结点的是父结点的右链接，这就是一个错误的 3- 结点，但一次左旋转就能够修正它

2.8 向一棵双键树（即一个 3- 结点）中插入新键

这种情况又可分为三种子情况：新键小于树中的两个键、在两者之间、或是大于树中的两个键。每种情况中都会产生一个同时连接到两条红链接的结点，而我们的目标就是修正这一点

三者中最简单的情况是新键大于原树中的两个键，因此它被连接到 3- 结点的右链接。此时树是平衡的，根结点为中间大小的键，它有两条红链接分别和较小和较大的结点相连。如果我们将两条链接的颜色都由红变黑，那么我们就得到了一棵由三个结点组成、高为 2 的平衡树。它正好能够对应一棵 2-3 树，如下图（左）
其他两种情况最终也会转化为这种情况。如果新键小于原树中的两个键，它会被连接到最左边的空链接，这样就产生了两条连续的红链接，如下图（中）。此时我们只需要将上层的红链接右旋转即可得到第一种情况（中值键为根结点并和其他两个结点用红链接相连）
如果新键介于原树中的两个键之间，这又会产生两条连续的红链接，一条红色左链接接一条红色右链接，如下图（右）。此时我们只需要将下层的红链接左旋转即可得到第二种情况（两条连续的红色左链接）

总的来说，我们通过 0 次、1 次和 2 次旋转以及颜色的变化得到了期望的结果

2.9 颜色转换

如下图所示，我们专门用一个方法 flipColors() 来转换一个结点的两个红色子结点的颜色。除了将子结点的颜色由红变黑之外，我们同时还要将父结点的颜色由黑变红。这项操作最重要的性质在于它和旋转操作一样是局部变换，不会影响整棵树的黑色平衡性。根据这一点，我们马上能够在下面完整地实现红黑树

2.10 根结点总是黑色

在前面所述的情况中，颜色转换会使根结点变为红色。这也可能出现在很大的红黑树中。严格地说，红色的根结点说明根结点是一个 3- 结点的一部分，但实际情况并不是这样。因此我们在每次插入后都会将根结点设为黑色。注意，每当根结点由红变黑时树的黑链接高度就会加 1

2.11 向树底部的 3- 结点插入新键

现在假设我们需要在树的底部的一个 3- 结点下加入一个新结点。前面讨论过的三种情况都会出现

指向新结点的链接可能是 3- 结点的右链接（此时我们只需要转换颜色即可)，或是左链接（此时我们需要进行右旋转然后再转换颜色)，或是中链接（此时我们需要先左旋转下层链接然后右旋转上层链接，最后再转换颜色）。颜色转换会使到中结点的链接变红，相当于将它送入了父结点。这意味着在父结点中继续插人一个新键，我们也会继续用相同的办法解决这个问题

2.12 将红链接在树中向上传递

2-3 树中的插入算法需要我们分解 3- 结点，将中间键插入父结点，如此这般直到遇到一个 2- 结点或是根结点

我们所考虑过的所有情况都正是为了达成这个目标：每次必要的旋转之后我们都会进行颜色转换，这使得中结点变红。在父结点看来，处理这样一个红色结点的方式和处理一个新插入的红色结点完全相同，即继续把红链接转移到中结点上去

上图中总结的三种情况显示了在红黑树中实现 2-3 树的插入算法的关键操作所需的步骤：要在一个3-结点下插入新键，先创建一个临时的 4- 结点，将其分解并将红链接由中间键传递给它的父结点。重复这个过程，我们就能将红链接在树中向上传递，直至遇到一个 2- 结点或者根结点

总之，只要谨慎地使用左旋转、右旋转和颜色转换这三种简单的操作，我们就能够保证插入操作后红黑树和 2-3 树的一一对应关系。在沿着插入点到根结点的路径向上移动时在所经过的每个结点中顺序完成以下操作，我们就能完成插入操作：

如果右子结点是红色的而左子结点是黑色的，进行左旋转
如果左子结点是红色的且它的左子结点也是红色的，进行右旋转
如果左右子结点均为红色，进行颜色转换

3 红黑树实现

3.1 插入

因为保持树的平衡性所需的操作是由下向上在每个所经过的结点中进行的，将它们植入我们已有的二叉查找树的实现中十分简单：只需要在递归调用之后完成这些操作即可，如下例（其中定义的 Node 类及 isRed() 等方法在前面均有给出，这里未再给出完整实现）

public class RedBlackBST<Key extends Comparable<Key>, Value> {
    
    
    private Node root;

    private class Node {
    
    
    } // 含有 color 变量的 Node 对象

    private boolean isRed(Node h) {
    
    
    }

    private Node rotateLeft(Node h) {
    
    
    }

    private Node rotateRight(Node h) {
    
    
    }

    private void flipColors(Node h) {
    
    
    }

    private int size() {
    
    
    }

    public void put(Key key, Value val) {
    
     // 查找key，找到则更新其值，否则为它新建一个结点
        root = put(root, key, val);
        root.color = BLACK;
    }

    private Node put(Node h, Key key, Value val) {
    
    
        if (h == null) // 标准的插入操作，和父结点用红链接相连
            return new Node(key, val, 1, RED);
        int cmp = key.compareTo(h.key);
        if (cmp < 0) h.left = put(h.left, key, val);
        else if (cmp > 0) h.right = put(h.right, key, val);
        else h.val = val;

        if (isRed(h.right) && !isRed(h.left)) h = rotateLeft(h);
        if (isRed(h.left) && isRed(h.left.left)) h = rotateRight(h);
        if (isRed(h.left) && isRed(h.right)) flipColors(h);
        h.N = size(h.left) + size(h.right) + 1;
        return h;
    }
}

前面列出的三种操作都可以通过一个检测两个结点的颜色的 if 语句完成。在检查了三到五个结点的颜色之后（也许还需要进行一两次旋转以及颜色转换），我们就可以得到一棵近乎完美平衡的二叉查找树

除了递归调用后的三条 if 语句,红黑树中 put() 的递归实现和二叉查找树中 put() 的实现完全相同。它们在查找路径上保证了红黑树和 2-3 树的一一对应关系，使得树的平衡性接近完美。第一条 if 语句会将任意含有红色右链接的 3- 结点（或临时的 4- 结点)向左旋转；第二条 if 语句会将临时的 4- 结点中两条连续红链接中的上层链接向右旋转；第三条 if 语句会进行颜色转换并将红链接在树中向上传递

下图是我们的标准索引测试用例进行测试的轨迹和用同一组键按照升序构造一棵红黑树的测试轨迹

3.2 删除

要描述删除算法，首先我们要回到 2-3 树。和插入操作一样，我们也可以定义一系列局部变换来在删除一个结点的同时保持树的完美平衡性。这个过程比插入一个结点更加复杂，因为我们不仅要在（为了删除一个结点而）构造临时 4- 结点时沿着查找路径向下进行变换，还要在分解遗留的 4- 结点时沿着查找路径向上进行变换（同插入操作)

3.2.1 自顶向下的 2-3-4 树

先学习一个沿查找路径既能向上也能向下进行变换的稍简单的算法：2-3-4 树的插入算法，2-3-4 树中允许存在我们以前见过的 4- 结点。它的插入算法沿查找路径向下进行变换是为了保证当前结点不是 4- 结点（这样树底才有空间来插入新的键），沿查找路径向上进行变换是为了将之前创建的 4- 结点配平

向下的变换和我们在 2-3 树中分解 4- 结点所进行的变换完全相同。如果根结点是 4- 结点，我们就将它分解成三个 2- 结点，使得树高加 1

在向下查找的过程中，如果遇到一个父结点为 2- 结点的 4- 结点，我们将 4- 结点分解为两个 2- 结点并将中间键传递给它的父结点，使得父结点变为一个 3- 结点；如果遇到一个父结点为 3- 结点的 4- 结点，我们将 4- 结点分解为两个 2- 结点并将中间键传递给它的父结点，使得父结点变为一个 4- 结点

我们不必担心会遇到父结点为 4- 结点的 4- 结点，因为插入算法本身就保证了这种情况不会出现。到达树的底部之后，我们也只会遇到 2- 结点或者 3- 结点，所以我们可以插入新的键。

要用红黑树实现这个算法，我们需要：

将 4- 结点表示为由三个 2- 结点组成的一棵平衡的子树，根结点和两个子结点都用红链接相连
在向下的过程中分解所有 4- 结点并进行颜色转换
和插入操作一样，在向上的过程中用旋转将 4- 结点配平

只需要移动 3.1 插入算法的 put() 方法中的一行代码就能实现 2-3-4 树中的插入操作：将 colorFlip() 语句（及其 if 语句）移动到递归调用之前（null 测试和比较操作之间）。在多个进程可以同时访问同一棵树的应用中这个算法优于 2-3 树，因为它操作的总是当前结点的一个或两个链接。我们下面要讲的删除算法和它的插入算法类似，而且也适用于 2-3 树

3.2.2 删除最小键

从树底部的 3- 结点中删除键是很简单的，但 2- 结点则不然。从 2- 结点中删除一个键会留下一个空结点，一般我们会将它替换为一个空链接，但这样会破坏树的完美平衡性

所以我们需要这样做：为了保证我们不会删除一个 2- 结点，我们沿着左链接向下进行变换，确保当前结点不是 2- 结点（可能是 3- 结点，也可能是临时的 4- 结点）。首先，根结点可能有两种情况。如果根是 2- 结点且它的两个子结点都是 2- 结点，我们可以直接将这三个结点变成一个 4- 结点；否则我们需要保证根结点的左子结点不是 2- 结点，如有必要可以从它右侧的兄弟结点“借”一个键来

在沿着左链接向下的过程中，保证以下情况之一成立：

如果当前结点的左子结点不是 2- 结点，完成
如果当前结点的左子结点是 2- 结点而它的亲兄弟结点不是 2- 结点，将左子结点的兄弟结点中的一个键移动到左子结点中
如果当前结点的左子结点和它的亲兄弟结点都是 2- 结点，将左子结点、父结点中的最小键和左子结点最近的兄弟结点合并为一个 4- 结点，使父结点由 3- 结点变为 2- 结点或者由 4- 结点变为 3- 结点

在遍历的过程中执行这个过程，最后能够得到一个含有最小键的 3- 结点或者 4- 结点，然后我们就可以直接从中将其删除，将 3- 结点变为 2- 结点，或者将 4- 结点变为 3- 结点。然后我们再回头向上分解所有临时的 4- 结点

3.2.3 删除操作

在查找路径上进行和删除最小键相同的变换同样可以保证在查找过程中任意当前结点均不是 2- 结点。如果被查找的键在树的底部，我们可以直接删除它。如果不在，我们需要将它和它的后继结点交换，就和二叉查找树一样。因为当前结点必然不是 2- 结点，问题已经转化为在一棵根结点不是 2- 结点的子树中删除最小的键，我们可以在这棵子树中使用前文所述的算法。和以前一样，删除之后我们需要向上回溯并分解余下的 4- 结点

3.3 红黑树的性质

研究红黑树的性质就是要检查对应的 2-3 树并对相应的 2-3 树进行分析的过程。我们的最终结论是所有基于红黑树的符号表实现都能保证操作的运行时间为对数级别（范围查找除外，它所需的额外时间和返回的键的数量成正比）

3.3.1 性能分析

首先，无论键的插入顺序如何，红黑树都几乎是完美平衡的。这从它和 2-3 树的一一对应关系以及 2-3 树的重要性质可以得到

一棵大小为 N 的红黑树的高度不会超过 2lgN

红黑树的最坏情况是它所对应的 2-3 树中构成最左边的路径结点全部都是 3- 结点而其余均为 2- 结点。最左边的路径长度是只包含 2- 结点的路径长度（～ lgN）的两倍。要按照某种顺序构造一棵平均路径长度为 2lgN 的最差红黑树虽然可能，但并不容易

这个上界是比较保守的。使用随机的键序列和典型应用中常见的键序列进行的实验都证明，在一棵大小为 N 的红黑树中一次查找所需的比较次数约为（1.00lgN-0.5）。另外，在实际情况下你不太可能遇到比这个数字高得多的平均比较次数，如下表所示

一棵大小为 N 的红黑树中，根结点到任意结点的平均路径长度为 ∼ 1.00lgN

和典型的二叉查找树相比，一棵典型的红黑树的平衡性是很好的。上表显示的数据表明 FrequencyCounter 在运行中构造的红黑树的路径长度（即查找成本）比初等二叉查找树低 40% 左右，和预期相符。自红黑树的发明以来，无数的实验和实际应用都印证了这种性能改进

以使用 FrequencyCounter 在处理长度大于等于 8 的单词时 put() 操作的成本为例，平均成本降低得更多。这又一次验证了理论模型所预测的对数级别的运行时间，只不过这次的惊喜比二叉查找树的小，因为一棵大小为 N 的红黑树的高度不会超过 2lgN 已经向我们保证了这一点。节约的总成本低于在查找上节约的 40% 的成本，因为除了比较我们也统计了旋转和颜色变换的次数

红黑树的 get() 方法不会检查结点的颜色，因此平衡性相关的操作不会产生任何负担；因为树是平衡的，所以查找比二叉查找树更快。每个键只会被插入一次，但却可能被查找无数次，因此最后我们只用了很小的代价（和二分查找不同，我们可以保证插入操作是对数级别的）就取得了和最优情况近似的查找时间（因为树是接近完美平衡的，且查找过程中不会进行任何平衡性的操作）

查找的内循环只会进行一次比较并更新一条链接，非常简短，和二分查找的内循环类似（只有比较和索引运算）。这是我们见到的第一个能够保证对数级别的查找和插入操作的实现，它的内循环更紧凑。它通过了各种应用的考验，包括许多库实现

3.3.2 有序符号表 API

红黑树最吸引人的一点是它的实现中最复杂的代码仅限于 put()（和删除）方法。二叉查找树中的查找最大和最小键、select()、rank()、floor()、ceiling() 和范围查找方法不做任何变动即可继续使用，因为红黑树也是二叉查找树而这些操作也不会涉及结点的颜色

这些方法都能从红黑树近乎完美的平衡性中受益，因为它们最多所需的时间都和树高成正比。因此命题 G 和命题 E 一起保证了所有操作的运行时间是对数级别的

命题 I：在一棵红黑树中，以下操作在最坏情况下所需的时间是对数级别的：查找（get()）、插入（put()）、查找最小键、查找最大键、floor()、ceiling()、rank()、select()、删除最小键（deleteMin()）、删除最大键（deleteMax()）、删除（delete()）和范围查询（range()）

证明：我们已经讨论过 put()、get() 和 delete() 方法。对于其他方法，代码可以从二叉查找树中照搬（它们不涉及结点颜色）。命题 G 和命题 E 可以保证算法是对数级别的，所有操作在所经过的结点上只会进行常数次数的操作也说明了这一点

各种符号表实现的性能总结如下表所示：

这样的保证是一个非凡的成就。在信息世界的汪洋大海中，表的大小可能上千亿，但我们仍能够确保在几十次比较之内就完成这些操作

（左倾）红黑树推演总结