机器学习笔记（五）逻辑回归 、决策边界、OvR、OvO

1、分类问题

机器学习中有三大问题，分别是回归、分类和聚类。线性回归属于回归任务，而逻辑回归和k近邻算法属于分类任务。逻辑回归算法主要应用于分类问题，比如垃圾邮件的分类（是垃圾邮件或不是垃圾邮件），或者肿瘤的判断（是恶性肿瘤或不是恶性肿瘤）。在二分类的问题中，我们经常用 1 表示正向的类别，用 0 表示负向的类别。

2、逻辑回归

logistic回归是广义线性回归，因此与线性回归有很多相同之处。它们的模型形式基本上相同，都具有$\hat{y}=wx+b$，其中w和b是待求参数。其区别在于他们的值域不同，线性回归的值域在$[+\infty ,-\infty ]$，logistic回归值域在$[0,1]$。逻辑回归既可以看做是回归算法，也可以看做是分类算法，通常作为分类算法用，只可以解决二分类问题。回归问题怎么解决分类问题啦？作为分类任务时，我们将样本的特征和样本发生的概率联系起来，概率就是一个[0,1]之间的数。将$\hat{p}\ge 0.5$归为正例 1，将概率$\hat{p}\le 0.5$归为负例 0。
$$\hat{p}=f(x)\hat{y}=\{\begin{array}{rlr}1,& & \hat{p}\ge 0.5\\ 0,& & \hat{p}\le 0.5\end{array}$$
那么逻辑回归既然与线性回归有千丝万缕的联系，那它是怎么将线性回归的值域$[+\infty ,-\infty ]$约束到
$[0,1]$之间的一个概率值？线性回归问题中的假设函数$\hat{y}={\theta }^{T}x$，而想要其输出值满足$0\le \hat{y}\le 1$，引进sigmoid函数，如下所示：
$$sigmoid(x)=\frac{1}{1+e^{-x}}x={\theta }^{T}x$$
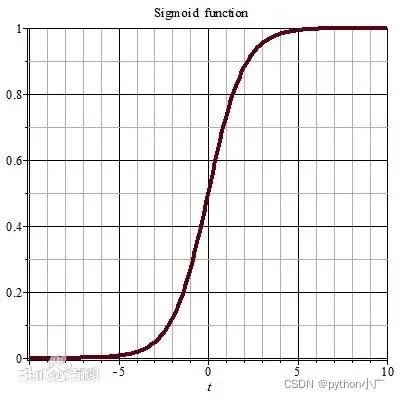
sigmoid函数图像如下所示，由函数图像可知，sigmoid函数能够满足逻辑回归的基本要求，其值域为$(0,1)$ 在$x>0$时，$\hat{p}>0.5$，在$x<0$时，$\hat{p}<0.5$。因此逻辑回归问题中的假设函数：
$$\hat{p}=sigmoid({\theta }^T\cdot x_{)}=\frac{1}{1+e^{-{\theta }^T\cdot x}}\hat{y}=\{\begin{array}{rlr}1,& & \hat{p}\ge 0.5\\ 0,& & \hat{p}\le 0.5\end{array}$$

3、损失函数

• 代价函数的表示

对于给定的样本数据集X,y，我们如何找到参数$\theta$。与线性回归问题一样，寻找合适的$\theta$参数对于假设函数与训练集的拟合是非常重要的，而寻找损失函数的最小值无疑是至关重要的。那么问题来了，我们应该如何表示损失函数。对于逻辑回归我们要求cost满足如下要求即可：
$$cost=\{\begin{array}{rl}& 如果y=1，p越小，cost越大\\ & 如果y=0，p越大，cost越大\end{array}$$
此时此刻有没有想到高中学过的 $-log(x)$ 函数在$(0,1)$之间的取值图像，正好满足我们的要求，因此我们可以将cost表示如下：
$$cost=\{\begin{array}{rlrlrlr}& & -log(\hat{p})& & if& & y=1\\ & & -log(1-\hat{p})& & if& & y=0\end{array}⟺cost=-ylog(\hat{p})-(1-y)log(1-\hat{p})$$
根据$y=1$和$y=0$两种不同的情况，其代价函数的图像如下所示：

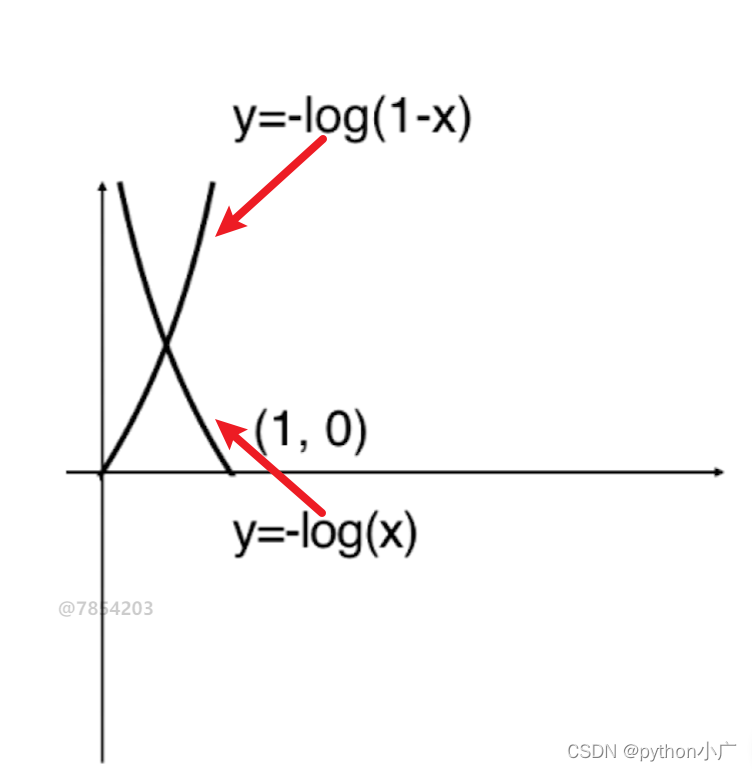
很容易发现，如果y=1时，对于$-log(x)$，取0时损失趋于$\infty$，取1则没有任何损失。而如果y=0时，对于$-log(1-x)$，取1时损失趋于$\infty$，取0则没有任何损失。此时我们便得到了逻辑回归的代价函数
$$J(\theta )=-\frac{1}{m}\sum _{i=1}^m{y}^{(i)}log(simgoid(X_b^{(i)}\theta ))+(1-y^{(i)})log(1-sigmoid(X_b^{(i)}\theta ))$$

• 代价函数的最小化
  与线性回归一样，得到代价函数之后，需要对代价函数求取最小值，仍然使用梯度下降算法，求解结果如下所示：
  $$\frac{J(\theta )}{{\theta }_j}=\frac{1}{m}\sum _{i=1}^m(simoid(X_b^{(i)})-y^{(i)})X_j^{(i)}$$
  $$\nabla J(\theta )=\frac{1}{m}\cdot \left[\begin{array}{c}\sum _{i=1}^m({\hat{y}}^{(i)}-y^{(i)})\cdot X_0^{(i)}\\ \sum _{i=1}^m({\hat{y}}^{(i)}-y^{(i)})\cdot X_1^{(i)}\\ \sum _{i=1}^m({\hat{y}}^{(i)}-y^{(i)})\cdot X_1^{(i)}\\ \cdots \\ \sum _{i=1}^m({\hat{y}}^{(i)}-y^{(i)})\cdot X_n^{(i)}\end{array}\right]=\frac{1}{m}\cdot X_b^T\cdot (sigmoid(X_b\theta )-y)$$
  $$其中X_b=\left[\begin{array}{ccccc}1& X_1^{(1)}& X_2^{(1)}& \cdots & X_n^{(1)}\\ 1& X_1^{(2)}& X_2^{(2)}& \cdots & X_n^{(2)}\\ \cdots & & & & \cdots \\ 1& X_1^{(m)}& X_2^{(m)}& \cdots & X_n^{(m)}\end{array}\right]\theta =\left[\begin{array}{ccccc}{\theta }_0& {\theta }_1& {\theta }_2& \cdots & {\theta }_n\end{array}\right]$$

4、决策边界

所谓决策边界就是能够把样本正确分类的一条边界，主要有线性决策边界和非线性决策边界。下面举一个栗子：
对于$sigmoid(x)$而言，当$x>0$时，预测的概率$p>0.5$，模型该该类分为1，当$x<0$时，预测的概率$p<0.5$，模型该该类分为0，模型在$x=0$成功将类别分开。而对于逻辑回归而言$x={\theta }^T\cdot x_b=0$，决策边界便是${\theta }^T\cdot x_b=0$的地方，如果X有两个特征：$${\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2=0\Rightarrow x_2=\frac{{\theta }_0-{\theta }_1{x}_1}{{\theta }_2}$$，我们将 $x_2用y表示，x_1用表示x，y=\frac{{\theta }_0-{\theta }_{1}x}{{\theta }_2}$我们便可以画出它的决策边界


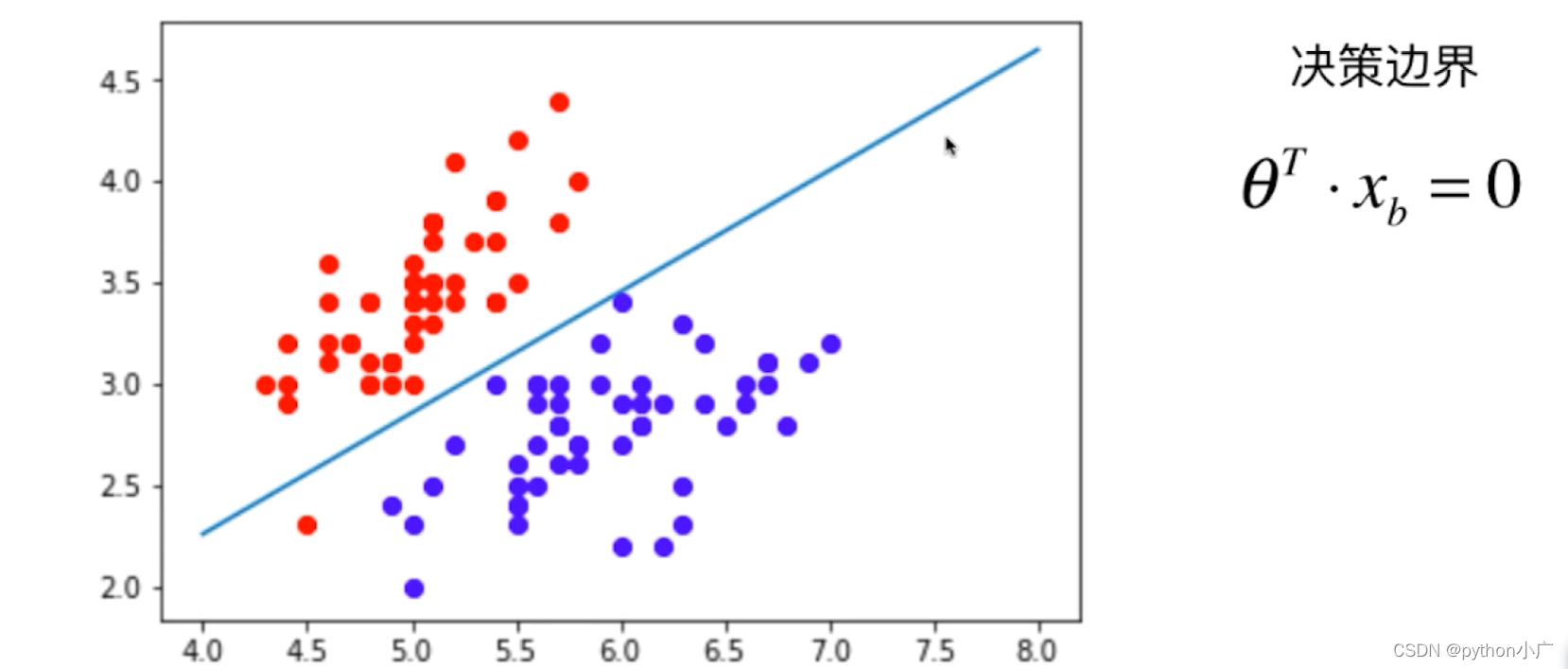
非线性决策边界

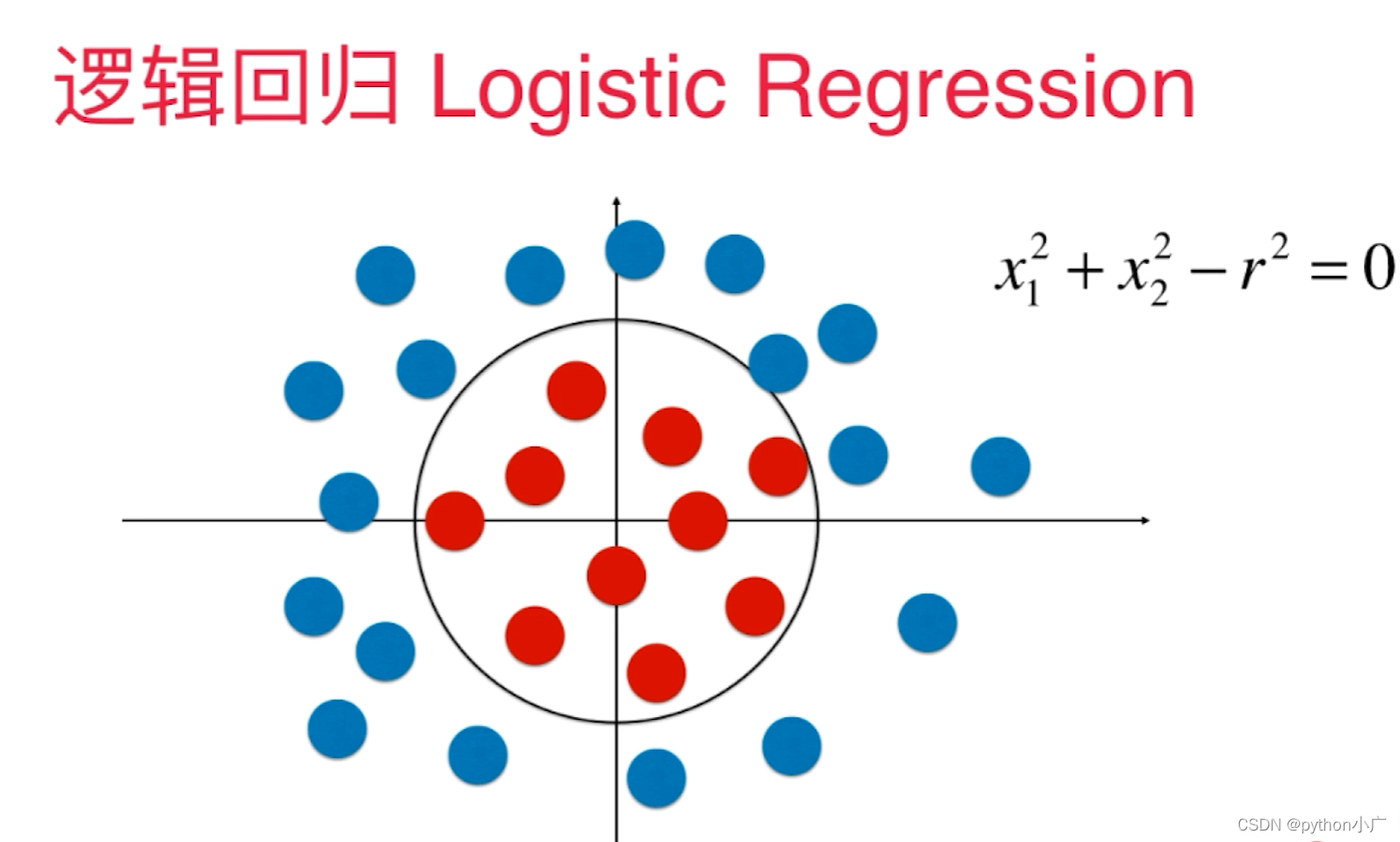
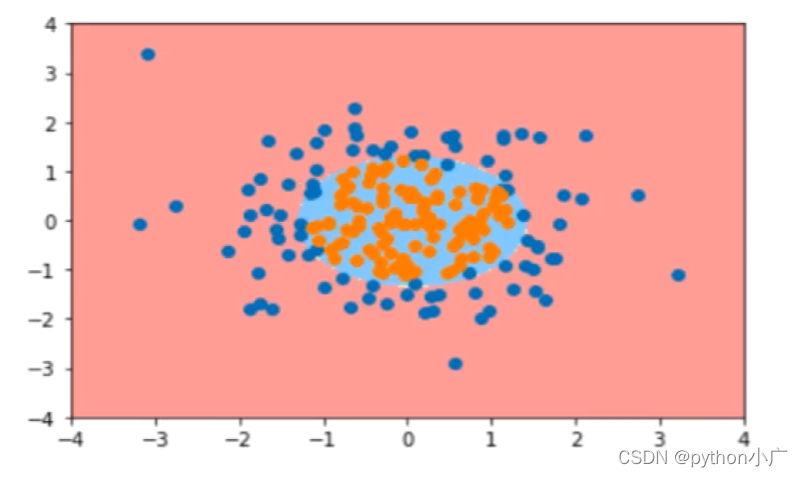
5、OvR与OvO

逻辑回归算法只能解决二分类问题，不过我们可以通过一些策略方法使逻辑回归算法同样能够解决多分类问题。让只能解决二分类问题的算法能够解决多分类的策略方法有两种：OvR和OvO。当然这两种方法不仅适用于逻辑回归算法，而是一种几乎能够改造所有二分类算法的通用方法。

• OvR（One vs Rest）

首先来看OvR（One vs Rest），通过OvR的英文名可以知道是一对剩余的所有，不过在其它一些机器学习教材或者资料中可能将OvR称为OvA（One vs All），它们两个表达的意思是一样的。不过称为OvR更为准确一些，并且在Sklearn文档中也是使用OvR命名的。
什么叫做一对剩余的所有呢？比如对于下图的四分类任务。

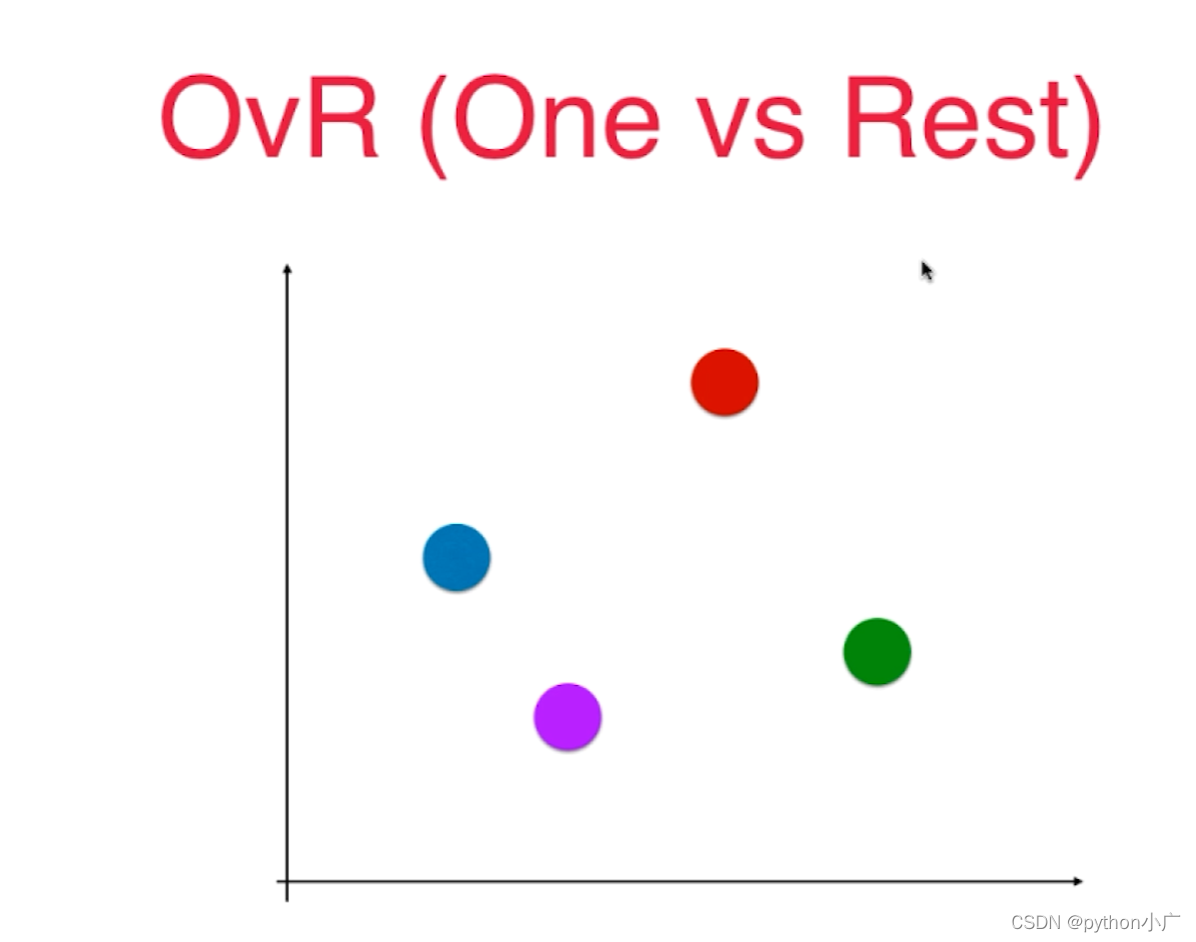
这里用四种不同颜色的点来代表四种不同的类别，很显然对于这样的四分类任务不能直接使用只能解决二分类问题的逻辑回归算法来处理。不过我们可以将其转换为二分类问题，相应的选取其中某一个类别，比如此时选择红色类别，而对于剩下的三个类别将它们称为其它类别，这也是One vs Rest的含义所在，红色类别为One剩下的所有类别为Rest。

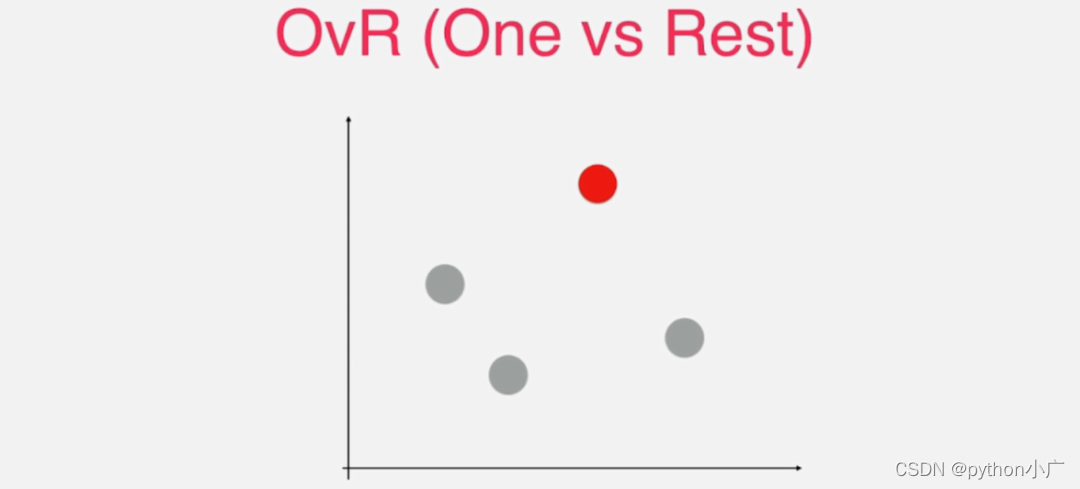
至此就将四分类问题转换成了二分类问题。当然这个转换二分类的过程不仅仅包含红色类别，还有其余三种类别对应的二分类，相对应的就会有四种二分类的情况。具体如下图所示。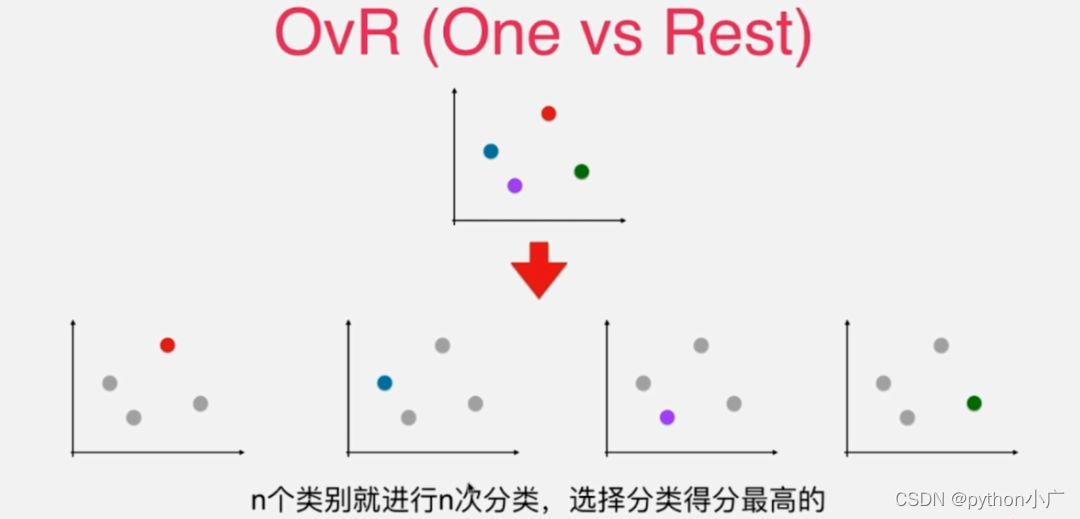

• OVO（One vs One）

OvO（One vs One），通过OvO的英文名可以知道是一对一的意思。这里依然使用拥有四个类别的四分类为例，每个类别用一个不同颜色的样本点来表示。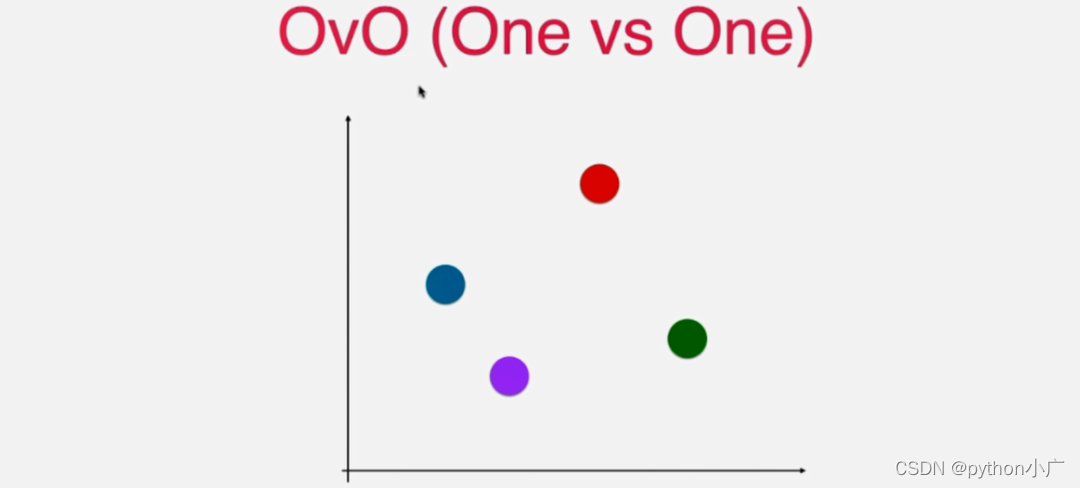
OvO就是每次直接挑选出其中的两个类别。比如这里挑出红色和蓝色这两个类别，然后对红色和蓝色两个类别进行二分类。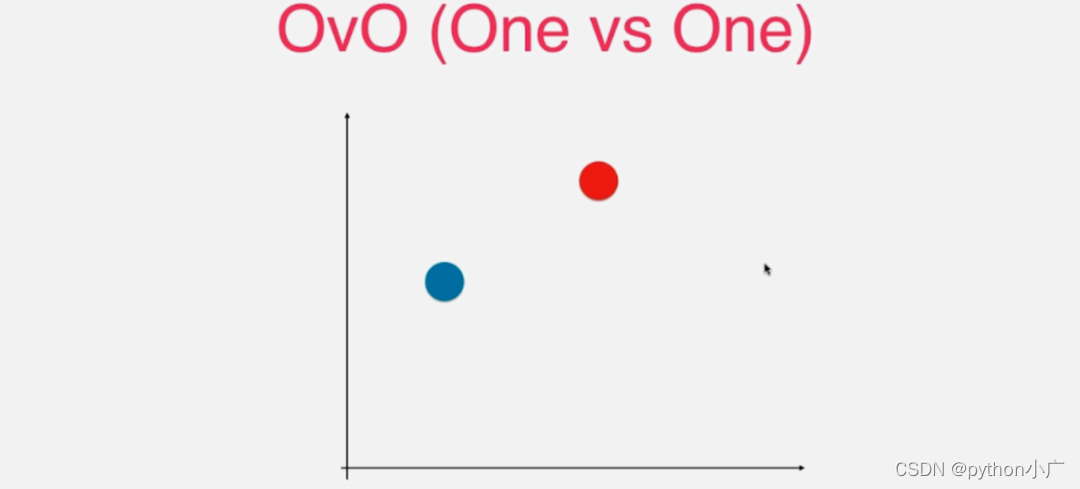
至此就将四分类的问题转换成了二分类问题。对于四分类来说，这个过程可以重复进行，四个类别每次选出两个类别，一共有 C(4, 2) = 6个不同两两类别对，也就是形成6个二分类任务。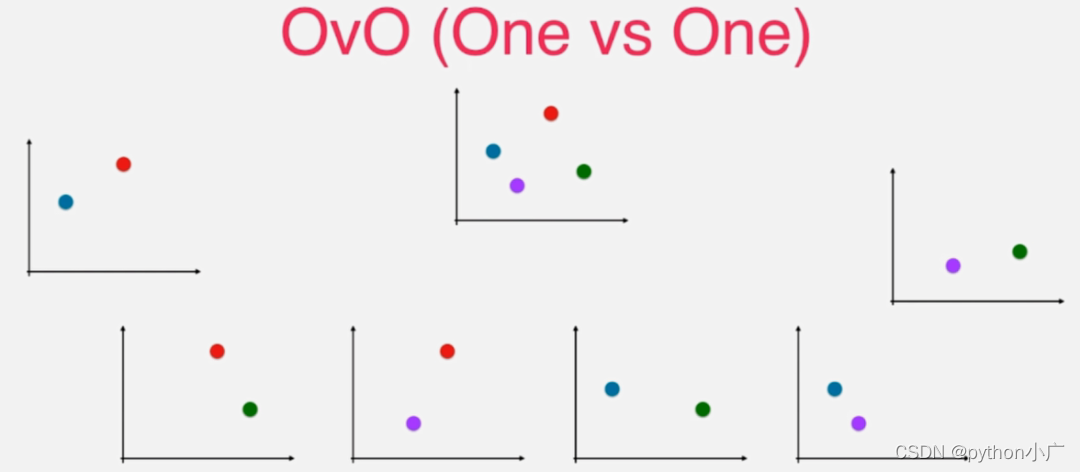
对于6个二分类问题，每一个二分类都可以估计出预测新样本属于对应两个类别中的哪一个类别，然后这6个分类结果进行投票选择分类结果数量最多的类别作为新样本点的类别。

参考：
https://cloud.tencent.com/developer/article/1605609