LIO-SAM中的scan_to_map原理剖析

残差构建和雅克比推导

最近在阅读LIO-SAM源码的时候，在它这个后端优化部分这里，scan_to_map里面涉及到了一些数学原理，这部分作者写得和LOAM很像，同样采用了欧拉角来推导残差和雅可比矩阵，最后基于此构建增量方程进行求解。实际上在了解清楚原理之后，再去看这部分的源码的时候也是比较好理解的。因为这一部分相对来说比较多的细节，所以这里单独一节记录下来。这部分对应的代码在 LIO-SAM/src/mapOptmization.cpp的scan2MapOptimization()函数中。

点线残差构建

点线残差的定义为点到线的距离，在该直线上取两个点 A=(x1,y1,z1), B=(x2,y2,z2)，设当前点为 P=(x0,y0,z0)，如下

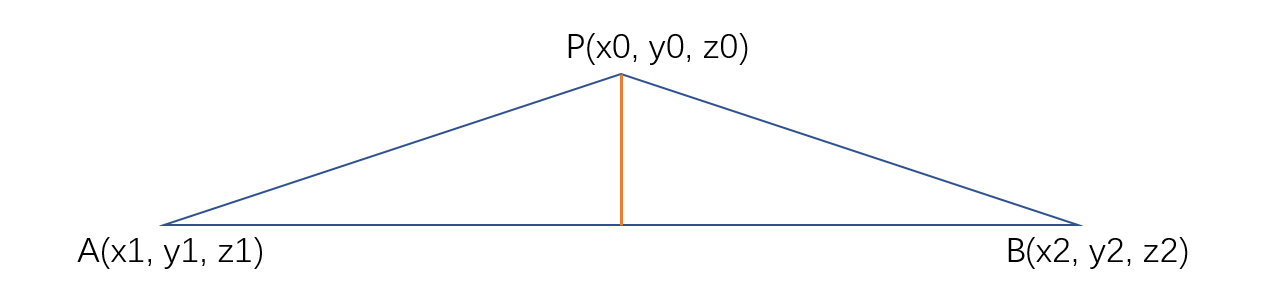
要计算点到直线的距离，只需要先计算三角形的面积，然后除以底边的模长即可

三角形面积计算
$$\begin{array}{rl}& S_{△ABP}\propto |\overrightarrow{PA}\times \overrightarrow{PB}|\\ & \overrightarrow{PA}\times \overrightarrow{PB}=\left|\begin{array}{ccc}i& j& k\\ x_1-x_0& y_1-y_0& z_1-z_0\\ x_2-x_0& y_2-y_0& z_2-z_0\end{array}\right|\\ & =\left|\begin{array}{c}\left(y_1-y_0\right)\left(z_2-z_0\right)-\left(z_1-z_0\right)\left(y_2-y_0\right)\\ \left(z_1-z_0\right)\left(x_2-x_0\right)-\left(x_1-x_0\right)\left(z_2-z_0\right)\\ \left(x_1-x_0\right)\left(y_2-y_0\right)-\left(y_1-y_0\right)\left(x_2-x_0\right)\end{array}\right|\\ & \mid \overrightarrow{PA}\times \overrightarrow{PB}\mid =(\overrightarrow{PA}\times \overrightarrow{PB}{)}^T(\overrightarrow{PA}\times \overrightarrow{PB})\\ & ={\left(\left(y_1-y_0\right)\left(z_2-z_0\right)-\left(z_1-z_0\right)\left(y_2-y_0\right)\right)}^2\\ & +{\left(\left(z_1-z_0\right)\left(x_2-x_0\right)-\left(x_1-x_0\right)\left(z_2-z_0\right)\right)}^2\\ & +{\left(\left(x_1-x_0\right)\left(y_2-y_0\right)-\left(y_1-y_0\right)\left(x_2-x_0\right)\right)}^2\end{array}$$
对应到代码中是：

// 计算 PA x PB 的模长
float a012 = sqrt(((x0 - x1)*(y0 - y2) - (x0 - x2)*(y0 - y1)) * ((x0 - x1)*(y0 - y2) - (x0 - x2)*(y0 - y1))     
            + ((x0 - x1)*(z0 - z2) - (x0 - x2)*(z0 - z1)) * ((x0 - x1)*(z0 - z2) - (x0 - x2)*(z0 - z1))    
            + ((y0 - y1)*(z0 - z2) - (y0 - y2)*(z0 - z1)) * ((y0 - y1)*(z0 - z2) - (y0 - y2)*(z0 - z1))); 

// 计算 AB 模长
float l12 = sqrt((x1 - x2)*(x1 - x2) + (y1 - y2)*(y1 - y2) + (z1 - z2)*(z1 - z2));

// P 到 AB 的距离
float ld2 = a012 / l12;

残差对点的雅可比矩阵

分为两步，先对点求导，再对位姿求导
$$J=\frac{\partial d}{\partial T_{wb}}=\frac{\partial d}{\partial {\mathbf{p}}^w}\frac{\partial {\mathbf{p}}^w}{\partial {\mathbf{T}}_{wb}}$$
设 ${\mathbf{p}}_m=\overrightarrow{PM}=\overrightarrow{PA}\times \overrightarrow{PB}$ ， 残差为:
$$\begin{array}{rl}& d\propto \sqrt{\begin{array}{l}{\left(\left(y_1-y_0\right)\left(z_2-z_0\right)-\left(z_1-z_0\right)\left(y_2-y_0\right)\right)}^2\\ +{\left(\left(z_1-z_0\right)\left(x_2-x_0\right)-\left(x_1-x_0\right)\left(z_2-z_0\right)\right)}^2\\ +{\left(\left(x_1-x_0\right)\left(y_2-y_0\right)-\left(y_1-y_0\right)\left(x_2-x_0\right)\right)}^2\end{array}}\\ & =\sqrt{{\mathbf{p}}_m^T{\mathbf{p}}_m}\\ & =\sqrt{\left(p_{mx}^2+p_{my}^2+p_{mz}^2\right)}\end{array}$$
得到残差的表达式之后，分别对(x0,y0,z0)求导可得
$$\begin{array}{rl}\frac{\partial d}{\partial {\mathbf{p}}^w}& ={\left[\begin{array}{l}\frac{\partial d}{\partial x_0}\\ \frac{\partial d}{\partial y_0}\\ \frac{\partial d}{\partial z_0}\end{array}\right]}^T\\ & \propto \frac{1}{2}{\left[\begin{array}{c}2p_{my}\left(\left(z_2-z_0\right)-\left(z_1-z_0\right)\right)+2p_{mz}\left(\left(y_1-y_0\right)-\left(y_2-y_0\right)\right)\\ 2p_{mz}\left(\left(x_2-x_0\right)-\left(x_1-x_0\right)\right)+2p_{mx}\left(\left(z_1-z_0\right)-\left(z_2-z_0\right)\right)\\ 2p_{mx}\left(\left(y_2-y_0\right)-\left(y_1-y_0\right)\right)+2p_{my}\left(\left(x_1-x_0\right)-\left(x_2-x_0\right)\right)\end{array}\right]}^T\\ & =\left[\begin{array}{l}{p}_{my}\left(z_2-z_1\right)+p_{mz}\left(y_1-y_2\right)\\ p_{mz}\left(x_2-x_1\right)+p_{mx}\left(z_1-z_2\right)\\ p_{mx}\left(y_2-y_1\right)+p_{my}\left(x_1-x_2\right)\end{array}\right]\end{array}$$
对应到代码中为

// 计算残差对点的雅可比矩阵并进行单位化
float la = ((y1 - y2)*((x0 - x1)*(y0 - y2) - (x0 - x2)*(y0 - y1)) 
            + (z1 - z2)*((x0 - x1)*(z0 - z2) - (x0 - x2)*(z0 - z1))) / a012 / l12;

float lb = -((x1 - x2)*((x0 - x1)*(y0 - y2) - (x0 - x2)*(y0 - y1)) 
             - (z1 - z2)*((y0 - y1)*(z0 - z2) - (y0 - y2)*(z0 - z1))) / a012 / l12;

float lc = -((x1 - x2)*((x0 - x1)*(z0 - z2) - (x0 - x2)*(z0 - z1)) 
             + (y1 - y2)*((y0 - y1)*(z0 - z2) - (y0 - y2)*(z0 - z1))) / a012 / l12;

点面残差构建

点到的平面的距离作为残差，对系数进行归一化处理，则计算方式为：
$$d_h=\frac{\left|pa\cdot x_0+pb\cdot y_0+pc\cdot z_0+pd\right|}{\sqrt{p{a}^2+p{b}^2+p{c}^2}}=\left|pa\cdot x_0+pb\cdot y_0+pc\cdot z_0+pd\right|$$

// 五个点组成5个约束，三个变量
Eigen::Matrix<float, 5, 3> matA0;
Eigen::Matrix<float, 5, 1> matB0;
Eigen::Vector3f matX0;

matA0.setZero();
matB0.fill(-1);
matX0.setZero();

// 要求距离都小于1m
if (pointSearchSqDis[4] < 1.0) {
    for (int j = 0; j < 5; j++) {  // 构建超定方程组
        matA0(j, 0) = laserCloudSurfFromMapDS->points[pointSearchInd[j]].x;
        matA0(j, 1) = laserCloudSurfFromMapDS->points[pointSearchInd[j]].y;
        matA0(j, 2) = laserCloudSurfFromMapDS->points[pointSearchInd[j]].z;
    }

    // 假设平面方程为ax+by+cz+1=0，这里就是求方程的系数abc，d=1
    matX0 = matA0.colPivHouseholderQr().solve(matB0);

    // 平面方程的系数，也是法向量的分量
    float pa = matX0(0, 0);
    float pb = matX0(1, 0);
    float pc = matX0(2, 0);
    float pd = 1;

    // 单位法向量
    float ps = sqrt(pa * pa + pb * pb + pc * pc);
    pa /= ps; pb /= ps; pc /= ps; pd /= ps;

    // 检查平面是否合格，如果5个点中有点到平面的距离超过0.2m，那么认为这些点太分散了，不构成平面
    bool planeValid = true;
    for (int j = 0; j < 5; j++) {
        if (fabs(pa * laserCloudSurfFromMapDS->points[pointSearchInd[j]].x +
                 pb * laserCloudSurfFromMapDS->points[pointSearchInd[j]].y +
                 pc * laserCloudSurfFromMapDS->points[pointSearchInd[j]].z + pd) > 0.2) {
            planeValid = false;
            break;
        }
    }

    // 平面合格
    if (planeValid) {
        // 当前激光帧点到平面距离
        float pd2 = pa * pointSel.x + pb * pointSel.y + pc * pointSel.z + pd;
        // 惩罚系数
        float s = 1 - 0.9 * fabs(pd2) / sqrt(sqrt(pointSel.x * pointSel.x
                                                  + pointSel.y * pointSel.y + pointSel.z * pointSel.z));

        // 点到平面垂线单位法向量（其实等价于平面法向量）
        coeff.x = s * pa;
        coeff.y = s * pb;
        coeff.z = s * pc;
        // 点到平面距离
        coeff.intensity = s * pd2;

        if (s > 0.1) {
            // 当前激光帧平面点，加入匹配集合中
            laserCloudOriSurfVec[i] = pointOri;
            // 参数
            coeffSelSurfVec[i] = coeff;
            laserCloudOriSurfFlag[i] = true;
        }
    }

残差对点的雅可比矩阵

根据残差的表达式
$$d_h=\frac{\left|pa\cdot x_0+pb\cdot y_0+pc\cdot z_0+pd\right|}{\sqrt{p{a}^2+p{b}^2+p{c}^2}}=\left|pa\cdot x_0+pb\cdot y_0+pc\cdot z_0+pd\right|$$
残差表达式分别对（x0,y0,z0）求导可以看出，雅可比矩阵就是平面的法向量，所以

// 用法向量作为雅可比，方向由 pd2 间接决定
coeff.x = s * pa;
coeff.y = s * pb;
coeff.z = s * pc;
coeff.intensity = s * pd2;

残差对位移的雅可比

因为
$$J=\frac{\partial d}{\partial T_{wb}}=\frac{\partial d}{\partial {\mathbf{p}}^w}\frac{\partial {\mathbf{p}}^w}{\partial {\mathbf{T}}_{wb}}$$
实际上我们要求的是
$$\mathrm{mat}A=\left[\begin{array}{c}\frac{\partial d}{\partial \text{ roll }}\\ \frac{\partial d}{\partial pitch}\\ \frac{\partial d}{\partial yaw}\\ \frac{\partial d}{\partial t_x}\\ \frac{\partial d}{\partial t_y}\\ \frac{\partial d}{\partial t_z}\end{array}\right]$$
通过上面的几步求得了残差对点的雅可比，下面求点对位姿的雅可比即可

设 Lidar 相对于世界坐标系旋转矩阵为R ，平移为t ，将 Lidar 坐标系下的点转为世界坐标系的过程为：
$${\mathbf{p}}^w=\mathbf{R}\mathbf{p}+\mathbf{t}$$
因为对平移的雅可比矩阵即为：
$$\frac{\partial p^w}{\partial t}=\frac{\partial \mathbf{R}p+t}{\partial t}=\mathbf{I}$$
所以
$$J_t=\frac{\partial d}{\partial t_{wb}}=\frac{\partial d}{\partial {\mathbf{p}}^w}\frac{\partial {\mathbf{p}}^w}{\partial \mathbf{t}}=\frac{\partial d}{\partial {\mathbf{p}}^w}$$
对应到代码中即为：

// 残差对位移的求导
matA.at<float>(i, 3) = coeff.z;
matA.at<float>(i, 4) = coeff.x;
matA.at<float>(i, 5) = coeff.y;

残差对旋转的雅可比

LOAM 原作者选择的是 ZXY 外旋（沿固定 Z 轴旋转-> 沿固定 X 轴旋转 -> 沿固定 Y 轴旋转）表示，这里作者也沿用了这种旋转方式，因此 ZXY 外旋的旋转矩阵的计算方式为：R=RyRxRz，即：
$$\begin{array}{rl}\mathbf{R}& ={\mathbf{R}}_y{\mathbf{R}}_x{\mathbf{R}}_z\\ & =\left[\begin{array}{ccc}\cos (ry)& 0& \sin (ry)\\ 0& 1& 0\\ -\sin (ry)& 0& \cos (ry)\end{array}\right]\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos (rx)& -\sin (rx)\\ 0& \sin (rx)& \cos (rx)\end{array}\right]\left[\begin{array}{ccc}\cos (rz)& -\sin (rz)& 0\\ \sin (rz)& \cos (rz)& 0\\ 0& 0& 1\end{array}\right]\\ & =\left[\begin{array}{ccc}\cos (ry)\cos (rz)+\sin (ry)\sin (rx)\sin (rz)& \cos (rz)\sin (ry)\sin (rx)-\cos (ry)\sin (rz)& \cos (rx)\sin (ry)\\ \cos (rx)\sin (rz)& \cos (rx)\cos (rz)& -\sin (rx)\\ \cos (ry)\sin (rx)\sin (rz)-\cos (rz)\sin (ry)& \cos (ry)\cos (rz)\sin (rx)+\sin (ry)\sin (rz)& \cos (ry)\cos (rx)\end{array}\right]\end{array}$$
又因为平移对旋转的求导为0，所以可以得到：

这里首先对rx进行求导
$$\frac{\partial (\mathbf{R}\mathbf{p})}{\partial rx}=\left[\begin{array}{c}(\sin (ry)\cos (rx)\sin (rz))p_x+(\cos (rz)\sin (ry)\cos (rx))p_y-(\sin (rx)\sin (ry))p_z\\ -(\sin (rx)\sin (rz))p_x-(\sin (rx)\cos (rz))p_y-(\cos (rx))p_z\\ (\cos (ry)\cos (rx)\sin (rz))p_x+(\cos (ry)\cos (rz)\cos (rx))p_y-(\cos (ry)\sin (rx))p_z\end{array}\right]$$
这里得到的是点对旋转的雅可比，再右乘以残差对点的雅可比即（coeff.x，coeff.y，coeff.z）即可得到残差对旋转的雅可比，在代码中就是：

float arx = (crx*sry*srz*pointOri.x + crx*crz*sry*pointOri.y - srx*sry*pointOri.z) * coeff.x
                      + (-srx*srz*pointOri.x - crz*srx*pointOri.y - crx*pointOri.z) * coeff.y
                      + (crx*cry*srz*pointOri.x + crx*cry*crz*pointOri.y - cry*srx*pointOri.z) * coeff.z;

同理，对ry的求导也是如法炮制：
$$\begin{array}{r}\frac{\partial (\mathbf{R}p)}{\partial ry}=\left[\begin{array}{c}(-\sin (ry)\cos (rz)+\cos (ry)\sin (rx)\sin (rz))p_x+(\cos (rz)\cos (ry)\sin (rx)+\sin (ry)\sin (rz))p_y+(\cos (rx)\cos (ry))p_z\\ 0\\ (-\sin (ry)\sin (rx)\sin (rz)-\cos (rz)\cos (ry))p_x+(-\sin (ry)\cos (rz)\sin (rx)+\cos (ry)\sin (rz))p_y-(\sin (ry)\cos (rx))p_z\end{array}\right]\end{array}$$
同样地，再右乘以残差对点的雅可比即（coeff.x，coeff.y，coeff.z）即可得到残差对旋转的雅可比，在代码中就是：

float ary = ((cry*srx*srz - crz*sry)*pointOri.x 
                      + (sry*srz + cry*crz*srx)*pointOri.y + crx*cry*pointOri.z) * coeff.x
                      + ((-cry*crz - srx*sry*srz)*pointOri.x 
                      + (cry*srz - crz*srx*sry)*pointOri.y - crx*sry*pointOri.z) * coeff.z;

同理，对rz的求导也是如法炮制：
$$\begin{array}{r}\frac{\partial (\mathbf{R}p)}{\partial rz}=\left[\begin{array}{c}(-\cos (ry)\sin (rz)+\sin (ry)\sin (rx)\cos (rz))p_x+(-\sin (rz)\sin (ry)\sin (rx)-\cos (ry)\cos (rz))p_y\\ (\cos (rx)\cos (rz))p_x-(\cos (rx)\sin (rz))p_y\\ (\cos (ry)\sin (rx)\cos (rz)+\sin (rz)\sin (ry))p_x+(-\cos (ry)\sin (rz)\sin (rx)+\sin (ry)\cos (rz))p_y\end{array}\right]\end{array}$$
同样地，再右乘以残差对点的雅可比即（coeff.x，coeff.y，coeff.z）即可得到残差对旋转的雅可比，在代码中就是：

float arz = ((crz*srx*sry - cry*srz)*pointOri.x + (-cry*crz-srx*sry*srz)*pointOri.y)*coeff.x
                      + (crx*crz*pointOri.x - crx*srz*pointOri.y) * coeff.y
                      + ((sry*srz + cry*crz*srx)*pointOri.x + (crz*sry-cry*srx*srz)*pointOri.y)*coeff.z;

构建增量方程

在得到残差对位姿的雅可比矩阵之后，就可以构建增量方程了，构建增量方程之后，使用QR分解的方式进行求解。这里还做了一个退化检测，如果检测到信息矩阵发生退化就会进入退化处理，对之前求解出来的解进行一个纠正。如下：

cv::transpose(matA, matAt);
matAtA = matAt * matA;
matAtB = matAt * matB;
// J^T·J·delta_x = -J^T·f QR分解进行求解
cv::solve(matAtA, matAtB, matX, cv::DECOMP_QR);

// 首次迭代，检查近似Hessian矩阵（J^T·J）是否退化，或者称为奇异，主要检查信息矩阵的奇异值是否过小
if (iterCount == 0) {
    cv::Mat matE(1, 6, CV_32F, cv::Scalar::all(0)); // 存放特征值
    cv::Mat matV(6, 6, CV_32F, cv::Scalar::all(0)); // 存放特征向量
    cv::Mat matV2(6, 6, CV_32F, cv::Scalar::all(0));
    cv::eigen(matAtA, matE, matV);  
    matV.copyTo(matV2);
    isDegenerate = false;
    float eignThre[6] = {100, 100, 100, 100, 100, 100};
    for (int i = 5; i >= 0; i--) {
        if (matE.at<float>(0, i) < eignThre[i]) {
            for (int j = 0; j < 6; j++) {
                matV2.at<float>(i, j) = 0;  // 对于奇异值过小的特征向量直接赋0
            }
            isDegenerate = true;
        } else {
            break;
        }
    }
    matP = matV.inv() * matV2;
}
if (isDegenerate)
{
    cv::Mat matX2(6, 1, CV_32F, cv::Scalar::all(0));
    matX.copyTo(matX2);
    matX = matP * matX2;   // 实际上就是对于奇异值过小的对应的解就直接赋0，其他解按原增量方程解出来是什么就是什么
}

更新位姿

上面求解得到增量位姿之后，最后一步把它叠加到之前我们通过IMU得到的那个初始值上作为一个scan_to_map的结果

// 更新当前关键帧全局位姿估计
transformTobeMapped[0] += matX.at<float>(0, 0);
transformTobeMapped[1] += matX.at<float>(1, 0);
transformTobeMapped[2] += matX.at<float>(2, 0);
transformTobeMapped[3] += matX.at<float>(3, 0);
transformTobeMapped[4] += matX.at<float>(4, 0);
transformTobeMapped[5] += matX.at<float>(5, 0);

总结

scan_to_map的目的是对我们从IMU里程计得到的 transformTobeMapped 当前帧位姿进行进一步优化。首先，我们用当前帧的特征点去局部地图（这个地图由时空上的近邻帧构成）中构建点到线的距离、点到面的距离，以此作为残差以优化当前帧位姿；然后，我们通过链式法则求残差对位移、旋转的雅可比矩阵；最后利用雅可比矩阵和观测（残差）构建增量方程，用QR分解求解方程得到增量解，叠加到transformTobeMapped 即得到了一个比从里程计来更准确的位姿。