一、全概率公式
1.引例

p(活着) = 0.5 * 0.8 + 0.5 * 0.3
花活着这一事件可以分为两种情况,一种是如果邻居记得浇水的情况下,花活着,另一种是如果邻居忘记浇水的
情况下,花活着。
2.全概率公式

二、贝叶斯公式
1.引例

p(邻居记得浇花 | 花活着) = (p(花活着|邻居记得浇花)* p(邻居记得浇水))/ (p(花活着|邻居记得浇花)*p(邻居记得浇水)+ p(花活着|邻居忘记浇花)*p(邻居忘记浇水)) = (0.8 * 0.5) / (0.8 * 0.5 + 0.3 * 0.5)
2.贝叶斯公式

三、朴素贝叶斯
1.概念
贝叶斯算法基于贝叶斯定理,有严谨的数学理论支撑,当假设各个样本相互独立的情况下时,构造出的贝叶斯算法就叫做朴素贝叶斯算法。
2.算法流程
(1)设数据集为D,其中每一个元组有n个属性,其中一个元组为X = {x1,x2,…,xn}
(2)假设一共有m类{C1,C2,…,Cm},给定元组X,计算X属于哪一类的概率最大,即P(Ci | X)最大时,X属于概率最大的Ci类。
根据贝叶斯公式,P(Ci | X) = (P(X | Ci)* P(Ci)) / P(X),其中P(X)可以由全概率公式得到。
(3)对于每一类Ci,P(X)都相同,只需使得分子最大,P(X | Ci)* P(Ci)最大,其中P(Ci)= |Ci| / |D|(即是类别Ci的元组数比上数据集总的元组数)。
(4)对于P(X | Ci),假设各个属性之间相互独立,
所以P(X | Ci)= P(X1 | Ci) * P(X2 | Ci) …P(Xn | Ci)
如果属性是离散属性,则其中P(X1 | Ci)= Ci中的第一个属性等于X1的元组个数比上D中Ci的元组个数。
如果属性是连续属性,则
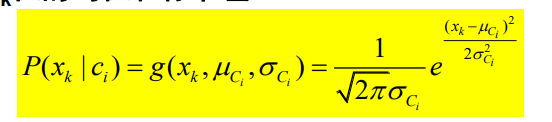
3.拉普拉斯校准
如果计算得到了某个P(Xj | Ci)= 0,会使得整个P(X | Ci)等于0,所以当数据样本过小时,如果某个属性的P(Xj | Ci)等于0,会抵消掉其他属性的影响,为了避免这种情况的发生,采用拉普拉斯平滑。
其中:
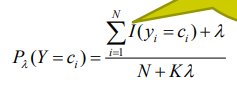
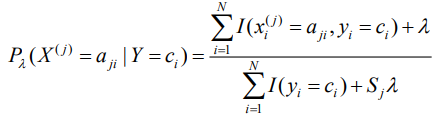
其中K代表种类个数,Sj代表第j个特征的取值个数,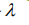 一般取1。
一般取1。
四、一个示例
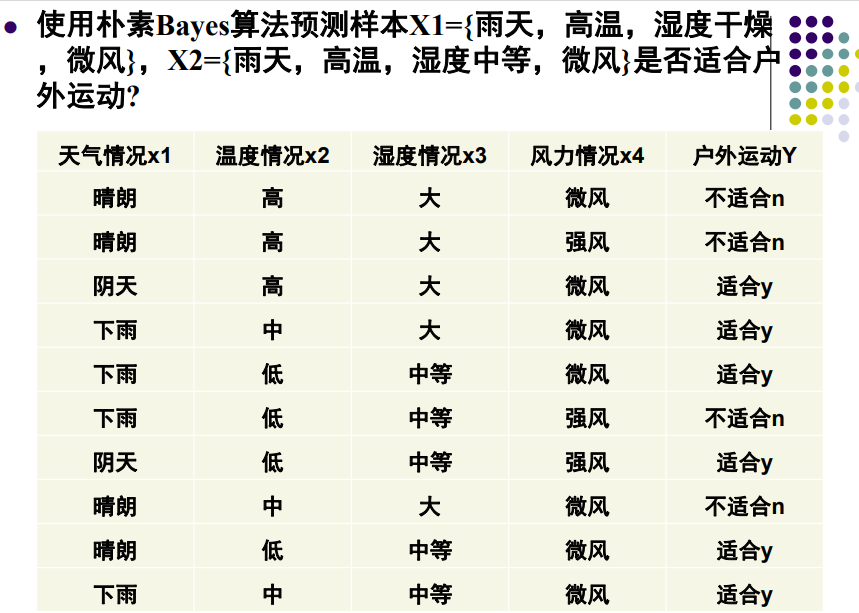


所以对于X1,X2都适合户外运动。