插值方法。

一、数学原理
⒈插值的定义
求一个简单函数φ(x)作为f(x)的近似表达式，以满足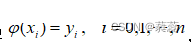
，我们称这样的问题为插值问题； 并称φ(x)为 f (x)的插值函数； f (x)为被插函数，x0 , x1, x2, …, xn是插值节(基)点。
⒉插值方法

以下为两种插值方法的特点比较，当插值节点相同时，无论何种方法得到的插值多项式本质上是相同的，即其插值曲线是重合的。

二、实验内容
设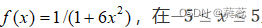
上按等距11个节点，画出牛顿插值函数曲线，分析当节点数较多时，构造的多项式与原函数的逼近关系。
程序实现：

format compact
clc,clear
fun=@(x)1./(1+6.*(x.*x));
fplot(fun,[-5,5]);
grid on
hold on
axis([-5.1 5.1 -0.5 1.5])

%牛顿插值法
x=-5:1:5;
y=fun(x);
m=length(x);
n=length(y);
if m~=n 
    error('向量x与y的长度必须一致');
end
% 计算差商表
k=2;
f(1)=y(1);
while k~=n+1
    f(1)=y(k);
    for i=1:k-1
        if i~=k-1
            f(i+1)=(f(i)-y(i))/(x(k)-x(i));
        else
            f(i+1)=(f(i)-y(i))/(x(k)-x(i));
        end
    end
    cs(i)=f(i+1);
    y(k)=f(k);
    k=k+1;
end
% 计算newton插值
x_i=-5:0.1:5;
p=length(x_i);
yi=zeros(1,p);
for k=1:p
    xi=x_i(k);
cfwh=0;
for i=1:n-1
    w=1;
    for j=1:i
        w=w*(xi-x(j));
    end
    cfwh=cfwh+cs(i)*w;
end
yi(k)=y(1)+cfwh;
end
plot(x_i,yi,'r--')
legend('实际曲线','牛顿插值', 'Location','NorthEast');

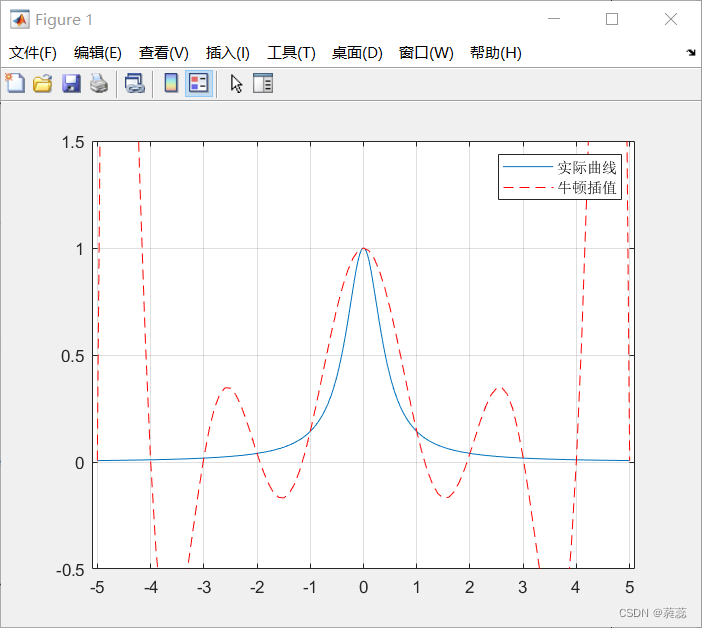
三、实验结果与分析

牛顿插值图：