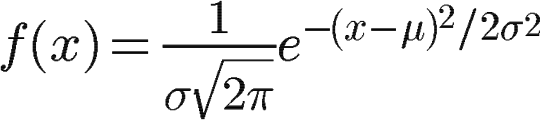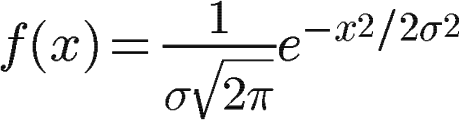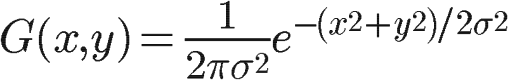通常,图像处理软件会提供"模糊"(blur)滤镜,使图片产生模糊的效果。
"模糊"的算法有很多种,其中有一种叫做"高斯模糊"(Gaussian Blur)。它将正态分布(又名"高斯分布")用于图像处理。
本文介绍"高斯模糊"的算法,你会看到这是一个非常简单易懂的算法。本质上,它是一种数据平滑技术(data smoothing),适用于多个场合,图像处理恰好提供了一个直观的应用实例。
1. 高斯模糊的原理
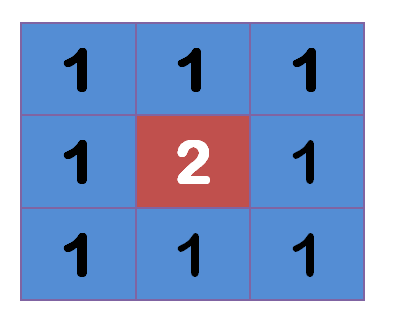
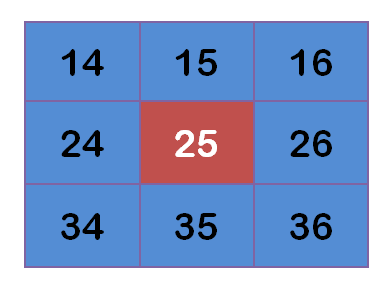
所谓"模糊",可以理解成每一个像素都取周边像素的平均值
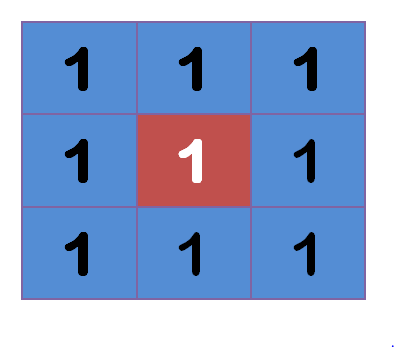
上图中,2是中间点,周边点都是1。
"中间点"取"周围点"的平均值,就会变成1。在数值上,这是一种"平滑化"。在图形上,就相当于产生"模糊"效果,"中间点"失去细节。
显然,计算平均值时,取值范围越大,"模糊效果"越强烈。
上面分别是原图、模糊半径3像素、模糊半径10像素的效果。模糊半径越大,图像就越模糊。从数值角度看,就是数值越平滑。
接下来的问题就是,既然每个点都要取周边像素的平均值,那么应该如何分配权重呢?
如果使用简单平均,显然不是很合理,因为图像都是连续的,越靠近的点关系越密切,越远离的点关系越疏远。因此,加权平均更合理,距离越近的点权重越大,距离越远的点权重越小。
2. 高斯分布(又名正态分布)的权重
正态分布显然是一种可取的权重分配模式。
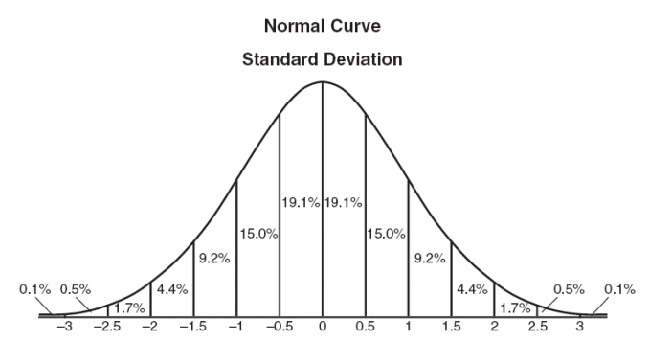
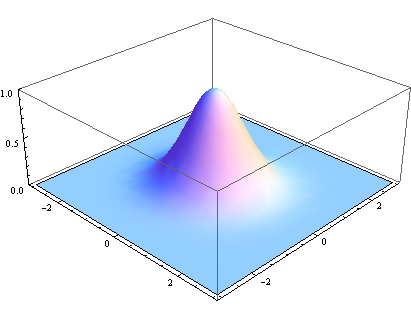
在图形上,正态分布是一种钟形曲线,越接近中心,取值越大,越远离中心,取值越小。
计算平均值的时候,我们只需要将"中心点"作为原点,其他点按照其在正态曲线上的位置,分配权重,就可以得到一个加权平均值。
3. 高斯分布及其概率密度函数
3.1 高斯分布及其概率密度函数定义

其概率密度函数又称为“高斯函数”。
如上所示,如果只有一个变量,称之为一维高斯分布,其概率密度函数称为一维高斯函数。
3.2 高斯函数各部分的意义
这里将能够对曲线产生影响的3个部分指代为a,b,c。
![]()
a具体公式为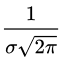 ,b公式为
,b公式为 ![]() 即均值,c表示
即均值,c表示![]() 即标准差。
即标准差。
a表示得到曲线的高度,b是指曲线在x轴的中心,c指width(与半峰全宽有关),图形如下:

3.3 3sigma的引入
再次回到这张图,这张图的横轴的0.5,1.5,2,2.5表示几个标准差大小,0.5即0.5个标准差大小,具体数值等于0.5sigma。1即1个标准差大小,具体数值为sigma,以此类推。其中19.1%表示分布在0-0.5sigma区间内占整个分布的19.1%,15%表示分布在0.5-1sigma区间内占整个分布的15%,以此类推。
这个分布可以一直取值,不停地向两边延伸,但是分了方便计算以及精度的考量,当我们取-3sigma到3sigma区间内时,此时该段区间内占整个分布的99.8%,我们就大致认为该段分布已经包含了所有的情况。(如果有理解错误请指正啊)
3.4 二维高斯函数的引入
一维高斯函数只能在一个方向上,而图像是二维的,此时引入二维高斯函数是一个很好地解决方案。
一维高斯函数的公式如下所示:
其中,μ是x的均值,σ是x的方差。因为计算平均值的时候,中心点就是原点,所以μ默认等于0。得到以下公式:
根据一维高斯函数,可以推导得到二维高斯函数:
有了这个函数 ,就可以计算每个点的权重了。
4. 高斯函数运用模糊的基本认识
将高斯核函数得出的卷积核模板称之为高斯核。
有了高斯函数的工具,那么怎么将他运用到图像中呢?
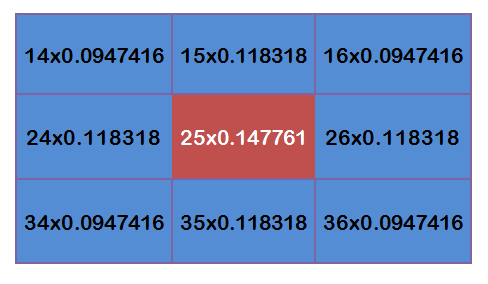
假设一个高斯函数的卷积和模板是5*5,那么他这25个点的x,y具体取值为:

此时只需要假定一个sigma值,即可确定一个高斯核。但是这个高斯核不完整,因为他求出的5*5的卷积核进行卷积操作时,改变了图像原始的0-255的范围。为解决该问题只需要将卷积核归一化即可,也就是卷积核中每一个值除以卷积的总和。
具体的高斯核例如:

4.1 实际使用的例子
假定中心点的坐标是(0,0),那么距离它最近的8个点的坐标如下:

远的点以此类推。
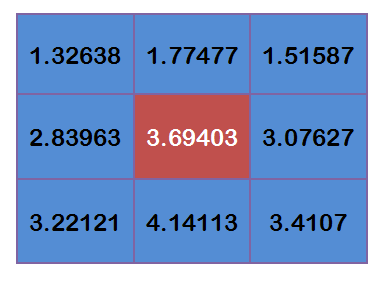
为了计算权重矩阵,需要设定σ的值。假定σ=1.5,则模糊半径为1的权重矩阵如下:

这9个点的权重总和等于0.4787147,如果只计算这9个点的加权平均,还必须让它们的权重之和等于1,因此上面9个值还要分别除以0.4787147,得到最终的权重矩阵。

有了权重矩阵,就可以计算高斯模糊的值了。
假设现有9个像素点,灰度值(0-255)如下:
每个点乘以自己的权重值:
得到
将这9个值加起来,就是中心点的高斯模糊的值。
对所有点重复这个过程,就得到了高斯模糊后的图像。如果原图是彩色图片,可以对RGB三个通道分别做高斯模糊。
5. 二维高斯核的可分离核形式
引入二维高斯核的可分离形式,主要是为了计算加速。
原始的卷积过程为:

这需要对矩阵切割,就是取一部分行取一部分列,影响执行速度。将高斯核分解为一个行向量和一个列向量的操作时,减少时间复杂度,能产生明显加速。
5.1 基本概念
此段内容参考: 二维高斯模糊和可分离核形式的快速实现_zxpddfg的专栏-CSDN博客_分离高斯模糊

上述中的高斯核为:
这和我们想象中的不一样,缺少了
这一项。
其实我们可以推导一下:

5.2 可分离核形式实现

其实
这个公式的由来也很简单:
那么高斯核矩阵又可以改写成归一化常数乘以一个列向量乘以一个行向量的形式,如下




5.3 实例分析
5.3.1 基本实现





5.4 符合局部性原则的内存访问加速


5.5 扩展与总结

6. 边界点的处理
如果一个点处于边界,周边没有足够的点,怎么办?
一个变通方法,就是把已有的点拷贝到另一面的对应位置,模拟出完整的矩阵。(其实这个在本文5.3.1 基本实现中已经有具体实例。)
7. 参考文献
[1] How to program a Gaussian Blur without using 3rd party libraries