机器学习——RBF神经网络

RBF神经网络

本文部分资料与案例来源：《MATLAB神经网络43个案例分析》

RBF神经网络简述

再介绍RBF神经网络之前我们先来看一下径向基函数（RBF），在百度百科上，RBF定义如下：

径向基函数是一个取值仅仅依赖于离原点距离的实值函数，也就是Φ（x）=Φ(‖x‖),或者还可以是到任意一点c的距离，c点称为中心点，也就是Φ（x，c）=Φ(‖x-c‖)。

简单来说，RBF就是一个表示空间中一点到中心点距离的函数，常用的RBF主要有以下几种：

而采取径向基函数作为激活函数的神经网络就是RBF神经网络，RBF神经网络是一种前向神经网络（信号一直向前传递不会返回），是一种三层的前向网络。RBF神经网络的第一层为输入层，由信号源节点组成；第二层为隐藏层，隐藏层中神经元变换函数即为径向基函数；第三层是输出层，它对模式输入做出响应。
上面这些文字可能有一些抽象，接下来我们以下图为例讲一讲RBF神经网络大概是个什么东西：
下图是一个简单的径向基神经网络模型：

从图中可以看到，径向基神经网络的激活函数是以输入向量和权值向量之间的距离作为自变量的。即输入隐藏层的数据为输入变量$\vec{X}=[x_1,x_2,\dots ,x_m]$与权值向量$\vec{W}=[w_1,w_2,\dots ,w_m]$的距离，一般取$||dist||=\sqrt{{\sum }_{i=1}^m(x_i-wi{)}^2}$。图中的b为阈值，当$||dist||$的值小于b时，将不会激活神经网络，用于调节神经网络的灵敏度；而权值向量$\vec{W}$就是我们找到的数据中心。

隐藏层的激活函数一般取高斯函数：$f(x)=e^{-\frac{1}{2{\sigma }^2}{x}^2}$，其中$\sigma$为
高斯函数的方差，是一个常数。隐藏层每个节点的输出就是输入的$||dist||$通过激活函数变换后的函数值。

至于输出y，由于这个模型只有一输出，隐藏层也只有一个结点，因此$y=e^{-\frac{1}{2{\sigma }^2}||dist|{|}^2}$

对于更为复杂一点的径向基神经网络，其隐藏层具有多个结点，其结构如下所示：

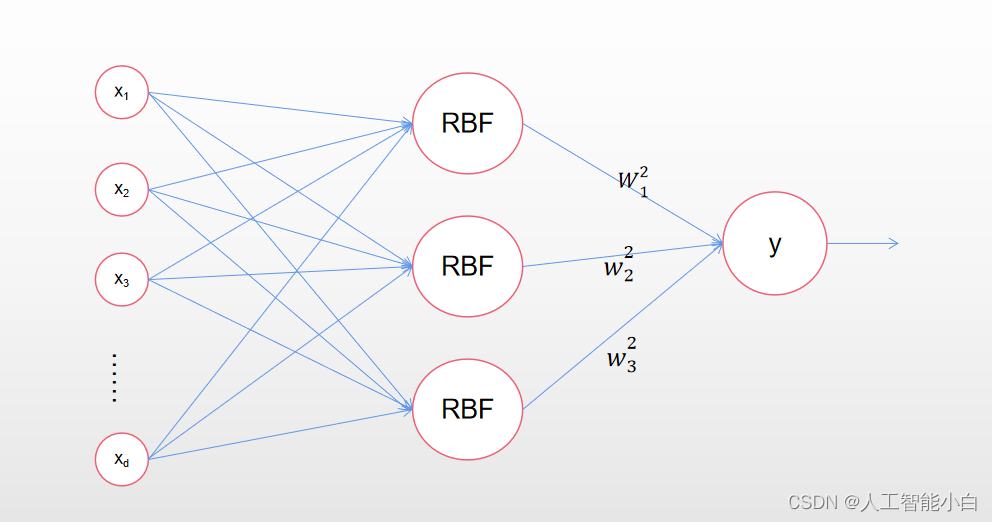
此时隐藏层有多个向输出层的输出，而输出层的输出则是隐藏层输出的线性加权平均，为了区别输入层的权值向量，我们用$w_i^2$表示第i个隐藏层结点的权值，于是输出层的输出为$y=output({\sum }_{i=1}^n{w}_i^{2}RBF(\vec{X},{\vec{W}}_i))$,${\vec{W}}_i$为第i个隐藏层结点的中心点向量，output()函数则需要根据不同的场景使用不同的函数，例如二分分类我们则可以使用sign()函数。
更为一般的神经网络结构则是隐藏层输出层都含有多个结点的结构，原理与上面的简单结构相差不大，这里就不在介绍。

RBF神经网络算法步骤

RBF神经网络学习算法需要求解的参数有三个：基函数的中心向量$\vec{W}$、方差$\sigma$以及隐含层到输出层的权值。根据选取的径向基函数中心的方法不同，RBF神经网络有不同的学习方式。下面将介绍自组织选取中心的RBF神经网络学习法。该方法由两个阶段组成：一是自组织学习阶段，此阶段为无导师学习过程，求解隐藏层基函数的中心向量与方差；二是有导师学习阶段，此阶段求解隐藏层到输出层之间的权值。

我们以高斯函数作为径向基神经网络的激活函数，则激活函数可以表示为：
$R({\vec{X}}^p-{\vec{W}}^i)=e^{-\frac{||{\vec{X}}^p-{\vec{W}}^i|{|}^2}{2{\sigma }^2}}$
$$\begin{gathered} w_i为高斯函数中心 \\ ||x_i-w_i||为欧式范数 \\ \sigma 为高斯函数方差 \\ {\vec{X}}^p=[x_1^p,x_2^p,\dots ,x_m^p]为第p个输入样本 \\ {\vec{W}}^i=[w_1^i,w_2^i,\dots ,w_m^i]为第i个隐藏层结点径向基函数的中心向量 \\ p=1,2,\dots ,P，P为样本总数 \end{gathered}$$

径向神经网络的输出为：
$y_j={\sum }_{i=1}^h{w}_{ij}^2{e}^{-\frac{||{\vec{X}}^p-{\vec{W}}^i|{|}^2}{2{\sigma }^2}}$
$$\begin{gathered} w_{ij}^2为隐藏层第i个结点到输出层第j个结点的权值 \\ i=1,2,\dots ,h为隐含层节点数 \\ {y}_j为神经网络的第j个输出结点的实际输出。 \end{gathered}$$
算法得具体步骤如下：
步骤1：基于K-均值聚类方法求取基函数中心：

1. 网络初始化：随机选取h个训练样本作为聚类中心$c_i(i=1,2,\dots ,h)$;
2. 将输入的训练样本集合按最近邻规则分组：即按照样本${\vec{X}}^p$与已选择得聚类中心之间的欧氏距离将样本分配到不同的集合${\varrho }_i(i=1,2,\dots ,h)中$；
3. 重新调整聚类中心：计算各个集合中训练样本得平均值，将这些均值作为新的聚类中心，如果新的聚类中心不在发生变化，则所得到的$c_i$即为神经网络的最终的基函数中心$W^i$，否则返回2进行下一轮中心求解。
   步骤二：求解方差$\sigma$:
   高斯函数的方差计算公式如下：
   $\sigma =\frac{W_{max}}{\sqrt{2h}}$
   $W_{max}为选取的聚类中心之间的最大距离，h为隐藏层结点个数$
   步骤3：计算隐藏层和输出层之间的权值：
   $w_{ij}=e^{\frac{h}{c_{max}^2}||{\vec{X}}^p-{\vec{W}}^i|{|}^2}，i=1,2,\dots ,h;p=1,2,\dots ,P$
   从上式中我们可以看出j=p，即输入样本数目等于输出结果数目。

使用RBF神经网络进行曲线拟合

其相关函数可以查阅Matlab文档：
newrb(P,T,goal,spread,MN,DF);
net = newrbe(P,T,spread);
A = radbas(N,FP);
代码如下：

%% Matlab神经网络43个案例分析
 
%% 清空环境变量
clc
clear
%% 产生训练样本（训练输入，训练输出）
% ld为样本例数
ld=400; 

% 产生2*ld的矩阵 
x=rand(2,ld); 

% 将x转换到[-1.5 1.5]之间
x=(x-0.5)*1.5*2; 

% x的第一行为x1，第二行为x2.
x1=x(1,:);
x2=x(2,:);

% 计算网络输出F值
F=20+x1.^2-10*cos(2*pi*x1)+x2.^2-10*cos(2*pi*x2);

%% 建立RBF神经网络 
% 采用approximate RBF神经网络。spread为默认值
net=newrb(x,F);

%% 建立测试样本

% generate the testing data
interval=0.1;
[i, j]=meshgrid(-1.5:interval:1.5);
row=size(i);
tx1=i(:);
tx1=tx1';
tx2=j(:);
tx2=tx2';
tx=[tx1;tx2];

%% 使用建立的RBF网络进行模拟，得出网络输出
ty=sim(net,tx);

%% 使用图像，画出3维图

% 真正的函数图像
interval=0.1;
[x1, x2]=meshgrid(-1.5:interval:1.5);
F = 20+x1.^2-10*cos(2*pi*x1)+x2.^2-10*cos(2*pi*x2);
subplot(1,3,1)
mesh(x1,x2,F);
zlim([0,60])
title('真正的函数图像')

% 网络得出的函数图像
v=reshape(ty,row);
subplot(1,3,2)
mesh(i,j,v);
zlim([0,60])
title('RBF神经网络结果')


% 误差图像
subplot(1,3,3)
mesh(x1,x2,F-v);
zlim([0,60])
title('误差图像')

set(gcf,'position',[300 ,250,900,400])