异或逻辑就是同1异0，而异或数据集顾名思义就是将二维坐标中的数据通过异或的逻辑方式划分为两类数据集。在二维坐标系下随机生成一些点，这些点作为数据总集合，点的数量就是数据集的数量，然后根据每个点的x坐标和y坐标的关系，对x坐标和u坐标做异或运算，得到值为1的点划分为一类，得到的值为0的点划分为另一类，这样得到的数据集就是需要的异或数据集。异或数据集是一类比较经典的非线性数据集。

创建一个简单的异或数据集，调用NumPy的logical_xor()函数形成一个异或门，其中将100个样本的分类标签设为1，100个样本的标签设为-1。

1）创建一个异或数据集的代码：

# 数据集及数据预处理

import matplotlib.pyplot as plt
import numpy as np
np.random.seed(1) # 随机数种子为1
X_xor = np.random.randn(200,2) # 形状为（200,2）的NumPy数组,包含200个随机生成的样本，每个样本有两个特征
y_xor = np.logical_xor(X_xor[:,0]>0, X_xor[:,1]>0) # 使用逻辑异或运算符创建形状为（200，）的NumPy数组,其中包含200个布尔值，表示X_xor中的每个样本是否满足一个或两个特征大于零
y_xor = np.where(y_xor, 1, -1) # 将y_xor中的所有True值替换为1，所有False值替换为-1，以创建一个包含标签的数组。
plt.scatter(X_xor[y_xor == 1,0], X_xor[y_xor == 1,1], c='b', marker='x', label='1')
plt.scatter(X_xor[y_xor == -1,0], X_xor[y_xor == -1,1], c='r', marker='s', label='-1')
plt.xlim([-3,3])
plt.ylim([-3,3])
plt.legend(loc='best')
plt.tight_layout()
plt.show()

2）代码执行效果

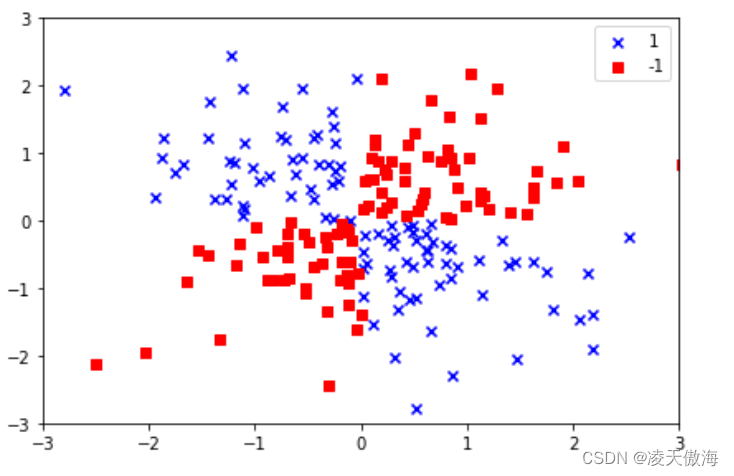
如上图所示，代码执行后会产生具有随机噪声的XOR数据集。

显然，异或数据集并不能产生线性超平面作为决策边界来分隔样本的正类和负类，接下来，将会利用支持向量机的核方法解决异或数据集的分类问题。

2、构建SVM分类器

核支持向量机解决非线性数据分类问题的核心就是通过映射函数ø将样本的原始特征映射到一个使样本线性可分的更高维的空间中。SVM算法的原理就是找到一个分割超平面，它能把数据正确地分类，并且间距最大。这里要实现的就是训练通过核支持向量机对非线性可分的异或数据集划分决策边界。

首先定义plot_decision_regions()函数绘制分类器的模型决策区域，并通过可视化的方法展示划分的效果。

1）划分区域的代码：

# 划分决策区域

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.colors import ListedColormap
def plot_decision_regions(x,y,model,resolution=0.02):
    """
    画出决策边缘的函数

    Parameters
    ----------
    x : array-like, shape (n_samples, n_features)
        训练集的输入特征
    y : array-like, shape (n_samples,)
        训练集的标签
    model : object
        训练好的分类器
    resolution : float, optional (default=0.02)
        网格的分辨率
    """
    
    # 定义标记和颜色
    markers = ('s', 'x', 'o', '^', 'v')
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    cmap = ListedColormap(colors[:len(np.unique(y))])
    
    # 计算网格的边界
    x1_min,x1_max = x[:,0].min() - 1, x[:,0].max() + 1
    x2_min,x2_max = x[:,1].min() - 1, x[:,1].max() + 1
    xx1,xx2 = np.meshgrid(np.arange(x1_min,x1_max,resolution), np.arange(x2_min,x2_max,resolution))    
    
    # 对网格上的点进行预测并绘制决策边缘
    z = model.predict(np.array([xx1.ravel(),xx2.ravel()]).T)
    z = z.reshape(xx1.shape)
    
    # 设置x轴和y轴的标签以及图例
    plt.contourf(xx1,xx2,z,alpha=0.4,cmap=cmap)
    plt.xlim(xx1.min(),xx1.max())
    plt.ylim(xx2.min(),xx2.max())
    
    # 绘制训练集的散点图

    plt.scatter(x_xor[y_xor == 1, 0], x_xor[y_xor == 1, 1], color='blue', marker='x', label='1')
    plt.scatter(x_xor[y_xor == -1, 0], x_xor[y_xor == -1, 1], color='red', marker='s', label='-1')
    plt.legend(loc='upper left')
    plt.xlabel("x1")
    plt.ylabel("x2")
    plt.show()

上述代码定义颜色和标记并通过ListedColormap()函数来从颜色列表创建色度图。然后通过NumPy的meshgrid()函数创建网格列阵xx1和xx2，利用特征向量确定特征的最小值和最大值，通过模拟足够多的数据绘制出决策边界。调用predict()函数来预测相应网格点的分类标签z，在把分类标签z改造成与xx1和xx2相同维数的网格后，调用Matplotlib的contourf()函数画出轮廓图。

2）求异或数据集决策边界的代码：

导入sklearn库中的SVC类，求出异或数据集的决策边界。

import numpy as np
from sklearn.svm import SVC

# 导入skleran库中的SVC类，求出异或数据集的决策边缘

if __name__ == '__main__':
    # 生成一个异或数据集
    x_xor = np.random.randn(200,2)
    y_xor = np.logical_xor(x_xor[:,0]>0,x_xor[:,1]>0)
    y_xor = np.where(y_xor,1,-1)
    
    # 训练一个径向基核的支持向量机
    svm = SVC(kernel='rbf',random_state=0,gamma=0.1,C=1.0)
    svm.fit(x_xor,y_xor)
    
    # 绘制决策边缘
    plot_decision_regions(x_xor, y_xor, svm)

其中，参数kernel='rbf'表示使用的核函数为高斯核函数，γ的值设置为0.1，也就是高斯球的截至参数，增大γ的值将加大训练样本的影响范围，导致决策边界紧缩或波动。

如果使用多项式核函数，可以将svm = SVC(kernel='rbf',random_state=0,gamma=0.1,C=1.0)这一行代码替换为svm = SVC(kernel='poly',degree=2,gamma=1,coef0=0)。其中，参数degree只对多项式核函数有用，是指多项式的核函数的阶数d，gamma为核函数系数，coef0是指多项式核函数中的常数项。可以看到多项式核函数需要调节的参数是比较多的。

三、案例结果及分析

1、高斯径向基核函数

1）使用径向基核函数，γ设置为0.1时，异或数据集的分类结果如下图所示

2）使用径向基核函数，γ设置为10时，异或数据集的分类结果如下图所示

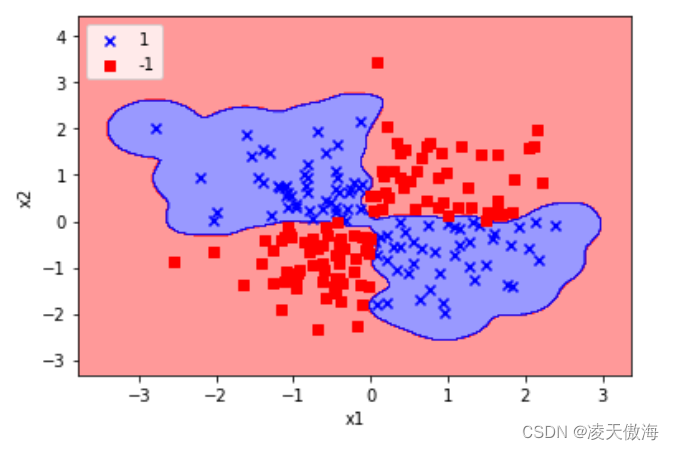
3）使用径向基核函数，γ设置为100时，异或数据集的分类结果如下图所示

2、多项式核函数

由于多项式核函数的参数比较多，在使用多项式核函数时，将参数degree固定为2，参数coef0的值固定为0，通过变化γ的值来观察可视化结果的变化。

1）使用多项式核函数，γ设置为0.1时，异或数据集的分类结果如下图所示

2）使用多项式核函数，γ设置为1时，异或数据集的分类结果如下图所示

3）使用多项式核函数，γ设置为100时，异或数据集的分类结果如下图所示

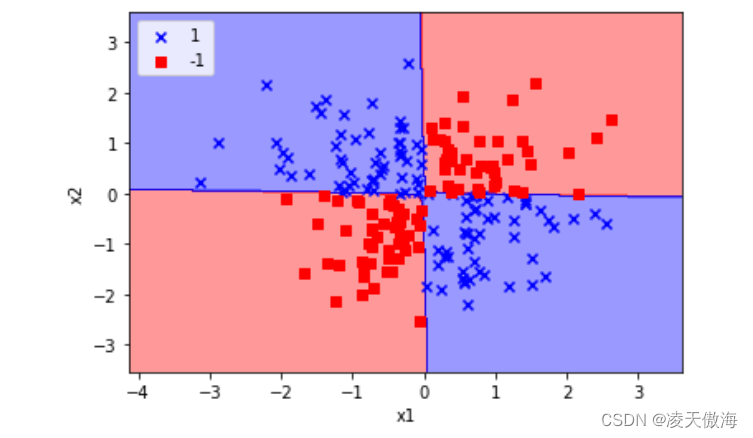
3 、总结

由上述结果可发现，γ的值比较小时，不同类别的决策边界比较宽松，γ值比较大时，不同类别的决策边界比较紧实，在使用高斯函数时，随着γ值的增大出现了过拟合的现象，说明γ在控制过拟合问题上也可以起到比较重要的作用。

对于两种核函数的不同决策结果，可以看到，两种核函数对于非线性分类的异或数据集的划分都有比较好的效果，而高斯函数由于参数比较少且分类结果比较稳定，因此在解决此类问题上可以优先选择高斯核函数。使用多项式核函数训练决策边界时，相同参数出现的结果可能会略有差异，这里设置多项式阶数为2，值比较小，训练速度比较快，如果阶数比较大，计算量会显著增加，将会使得训练时间比较长，这也是多项式核函数相对于高斯函数的一个小缺陷。

基于支持向量机（SVM）的异或数据集划分

一、支持向量机的简单介绍

1、什么是支持向量机

2、支持向量机的基本原理

3、常用核函数

4、SVM的优缺点

二、基于SVM的异或数据集划分

1、数据集及数据预处理