基于“FFD形变+梯度下降优化”图像配准的一种加速方法

前文我们讲过FFD形变与梯度下降优化算法的原理：

梯度下降法详解

图像配准系列之基于B样条的FFD自由变换原理与C++实现

图像配准系列之基于FFD形变与梯度下降法的图像配准

1. “FFD形变+梯度下降法”配准的主要耗时点

我们知道，基于“FFD形变+梯度下降优化”图像配准的核心思路是：

假设图像A为基准图像，图像B为浮动图像，使用FFD形变作为形变模型，对图像B进行形变，并计算图像A与形变之后的图像B的相似度，通过求解FFD形变的最优控制参数，使得两者相似度达到最大，然后使用最优控制参数对图像B进行形变，实现对其配准。

如下图所示，我们把图像A与FFD形变之后图像B的相似度作为目标函数，然后使用梯度下降法求解这个目标函数的最优解。

既然使用梯度下降法来求最优参数，那么就得求每个参数的梯度（偏导数）。假设目标函数f的输入参数为x1、x2、…、xn，那么其偏导数的定义为：

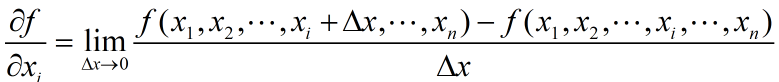
上式中Δx越接近0，所求值越接近偏导数的真实值，因此我们在实际计算时通常将Δx设置为一个较小值来计算梯度的近似值，如下式所示，EPS通常取0.1~0.5：

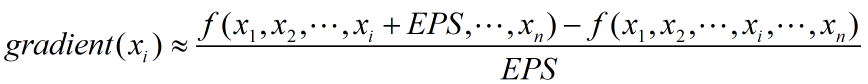
对于FFD形变模型，假设其有M*N个网格控制点，每个控制点有2个控制参数（x方向、y方向），因此总共有2*M*N个控制参数（输入参数）：x1、x2、…、x2*M*N。我们使用的相似度衡量指标为归一化互相关（NCC），那么目标函数f可以表示为：

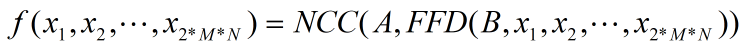
由上式可知，在梯度下降法的每轮迭代中我们需要计算2*M*N个输入参数的梯度，其中f(x1, x2, …, x2*M*N)只需要计算一次，f(x1, x2, …, xi+EPS, ..., x2*M*N)则需要计算2*M*N次，所以在每轮迭代中：

• 总共需要对浮动图像B执行2*M*N+1次FFD形变。

总共需要对图像A与经过FFD形变的图像B计算2*M*N次NCC。

以上就是“FFD形变+梯度下降法”配准的两个主要耗时点。在本文中我们将着重想办法来解决这两个主要耗时点，从而加速配准过程。

2. FFD形变的局部独立性特点

我们在前文讲过，FFD形变模型使用每个像素点周围4*4个控制点的控制参数来计算它的位置偏移，因此每个像素点形变之后的位置偏移只与它周围4*4个控制点有关，与其它控制点无关，这就是FFD形变的局部独立性特点。如下图所示，像素点A的形变由其周围4*4个控制点决定（从该点左上角开始数起）。

根据以上FFD形变的局部独立性特点，每一个控制点能影响的区域是有限的。如下图所示，对于控制点B，其只能影响橙色区域内像素点的形变偏移值，或者换一种说法，仅橙色区域内的像素点计算形变坐标偏移时才使用到控制点B的控制参数，橙色区域外的像素点均与控制点B无关。

因此我们由控制点B的网格坐标就可以把它影响的区域给确定下来，也即得到图像上被控制点B影响的区域的左上角、右下角坐标，实现代码如下：

#define BPLINE_BOARD_SIZE 3


//pos为控制点序号，比如有M*N个控制点，则pos的值为0~M*N之间的一个值
//row为图像高
//col为图像宽
//row_block_num+3为网格控制点的行数、col_block_num+3为网格控制点的列数
//x1、y1、x2、y2分别为影响区域的左上角x坐标、左上角y坐标、右下角x坐标、右下角y坐标
void cal_rect_area(int pos, int row, int col, int row_block_num, int col_block_num, int &x1, int &y1, int &x2, int &y2)
{
  int control_point_xx;
  int control_point_yy;
  int grid_cols = col_block_num + BPLINE_BOARD_SIZE;
  float delta_x = col*1.0 / col_block_num;
  float delta_y = row*1.0 / row_block_num;


  control_point_xx = pos % grid_cols;  //得到控制点的x网格坐标
  control_point_yy = pos / grid_cols;  //得到控制点的y网格坐标
  //根据上图，由控制点的网格坐标即可得到影响区域的左上角、右下角坐标
  //需要注意这里得到的是网格坐标，x、y需要分别乘以delta_x、delta_y转换为图像坐标
  x1 = floor((control_point_xx - 3)*delta_x);
  y1 = floor((control_point_yy - 3)*delta_y);
  x2 = floor((control_point_xx + 1)*delta_x);
  y2 = floor((control_point_yy + 1)*delta_y);
  //边界处理
  x1 = (x1 <= 0) ? 0 : (x1 + 1);
  y1 = (y1 <= 0) ? 0 : (y1 + 1);
  x2 = (x2 > col - 1) ? (col - 1) : x2;
  y2 = (y2 > row - 1) ? (row - 1) : y2;
}

下面我们做一个测试来验证我们得到的控制点影响区域是否正确：

• 首先初始化(25+3)*(25+3)个网格点的2*(25+3)*(25+3)个控制参数，使用这些参数对Lena图像进行FFD形变，得到形变图像I1；

• 然后改变2*(25+3)*(25+3)个控制参数中的第pos个控制参数的值，并对Lena图像进行FFD形变，得到形变图像I2；

• 计算I1和I2的差值图diff；

• 调用以上cal_rect_area函数获取第pos个控制参数的影响区域，并与差值图的差异区域进行比较，看是否一致。

代码如下：

void ffd_area_test(void)
{
  Mat img = imread("lena.jpg", CV_LOAD_IMAGE_GRAYSCALE);


  int row_block_num = 25;
  int col_block_num = 25;
  Mat grid_points;
  //初始化控制参数
  init_bpline_para(img, row_block_num, col_block_num, grid_points, -10, 10);


  Mat I1;
  //计算I1
  Bspline_Ffd(img, I1, row_block_num, col_block_num, grid_points);
  
  int pos = 550;  //修改第550个控制参数


  grid_points.ptr<float>(0)[pos] += 150.5;
  Mat I2;
  //计算I2
  Bspline_Ffd(img, I2, row_block_num, col_block_num, grid_points);


  Mat diff = abs(I1- I2);  //计算I1、I2的差值图


  int x1, y1, x2, y2;
  //获取第550个控制参数的影响区域
  cal_rect_area(pos, img.rows, img.cols, row_block_num, col_block_num, x1, y1, x2, y2);
  Mat area = Mat::zeros(img.size(), CV_8UC1);
  rectangle(area, Rect(x1, y1, x2 - x1, y2 - y1), Scalar(255, 255, 255), 2);


  imshow("I1", I1);
  imshow("I2", I2);
  imshow("diff", diff);
  imshow("area", area);
  waitKey();
}

运行结果如下，由此可知，我们调用函数cal_rect_area获取控制点的影响区域是正确的。

Lena原图

3. 梯度计算过程的加速

由以上章节可知，当改变某个控制点的1个控制参数的值时，仅影响该控制点周围局部区域的形变，局部区域之外的形变不受影响。而我们计算某个控制参数的梯度时，正是通过给该控制参数加上一个EPS来计算差分值，从而得到近似梯度值。因此我们计算梯度时可以利用FFD局部独立性的特点来加速计算。

假设改变控制参数之前图像B的FFD形变图像为I1，改变第i个控制参数之后图像B的FFD形变图像为I2。每轮迭代中I1只需要计算一次且保持不变，改变不同的控制参数得到的I2是各不相同的：

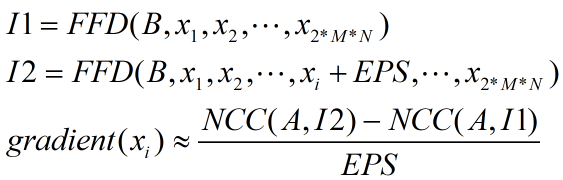
由上述的FFD局部独立性特点可知，I2与I1的区别并不大，区别仅仅在于改变控制参数的控制点周围的一小部分区域，所以我们计算I2时，只需要计算该影响区域的形变图像ΔI，然后再结合I1即可得到I2，而不需要计算整个图像B的形变图像。

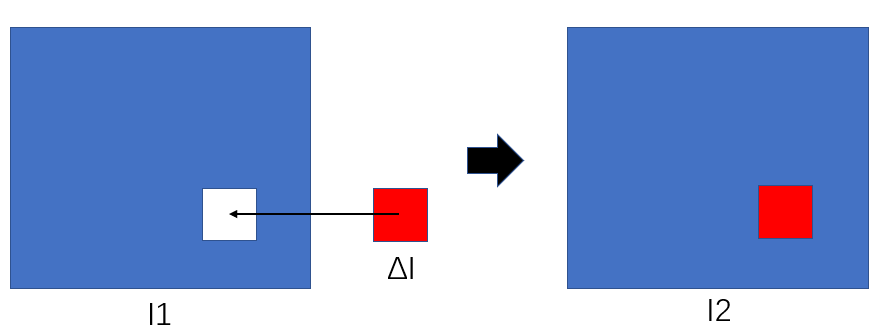
而且，计算NCC(A, I2)时也可以利用以上所说的局部独立性来加速计算。由于I2与I1的区别仅仅在形变图像ΔI，且每轮迭代中NCC(A, I1)只需计算一次且保持不变，因此可以使用NCC(A, I1)与ΔI来快速计算得到NCC(A, I2)。

假设图像A、B的尺寸都为m行n列，那么A、B的NCC的计算公式如下：

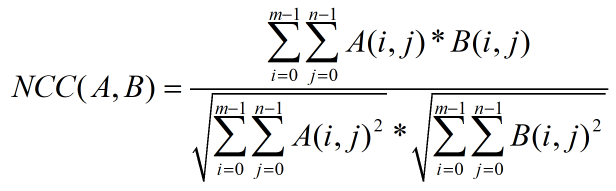
我们记：

所以有A、I1和A、I2的NCC计算公式：

由以上可知I2与I1的区别区域为一个很小的区域ΔI，ΔI的左上角、右下角坐标分别为(x1,y1)和(x2,y2)，那么有以下关系：

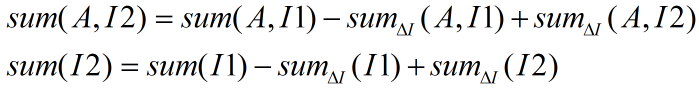
因此有下式，也即是NCC(A, I2)的快速计算式：

上式中：

实现代码：

获取I1与I2的区别区域代码：

void cal_rect_area(int pos, int row, int col, int row_block_num, int col_block_num, int &x1, int &y1, int &x2, int &y2)
{
  int control_point_xx;
  int control_point_yy;
  int grid_cols = col_block_num + BPLINE_BOARD_SIZE;
  float delta_x = col*1.0 / col_block_num;
  float delta_y = row*1.0 / row_block_num;


  control_point_xx = pos % grid_cols;
  control_point_yy = pos / grid_cols;


  x1 = floor((control_point_xx - 3)*delta_x);
  y1 = floor((control_point_yy - 3)*delta_y);
  x2 = floor((control_point_xx + 1)*delta_x);
  y2 = floor((control_point_yy + 1)*delta_y);


  x1 = (x1 <= 0) ? 0 : (x1 + 1);
  y1 = (y1 <= 0) ? 0 : (y1 + 1);
  x2 = (x2 > col - 1) ? (col - 1) : x2;
  y2 = (y2 > row - 1) ? (row - 1) : y2;
}

计算A、I1两张图像NCC的代码如下，计算之后把sum(A,I1)、sum(A)和sum(I1)保存下来，用于快速计算A、I2的NCC：

double cal_cc1(Mat S1, Mat Si, double &sum1, double &sum2, double &sum3)
{
  for (int i = 0; i < S1.rows; i++)
  {
    uchar *S1_data = S1.ptr<uchar>(i);
    uchar *Si_data = Si.ptr<uchar>(i);


    for (int j = 0; j < S1.cols; j++)
    {
      sum1 += S1_data[j] * S1_data[j];   //sum(A)
      sum2 += S1_data[j] * Si_data[j];  //sum(A,I1)
      sum3 += Si_data[j] * Si_data[j];  //sum(I1)
    }


  }
  //计算NCC的倒数作为目标函数值
  double cc1 = sqrt(sum1*sum3) / (sum2 + 0.0000001);


  return cc1;
}

快速计算A、I2的NCC代码：

//sum1、sum2、sum3由cal_cc1函数计算得到
double cal_cc2(Mat S1, Mat Si1, Mat Si2, int x1, int y1, int x2, int y2, double sum1, double sum2, double sum3)
{


  double sum2_i = sum2;
  double sum3_i = sum3;


  for (int i = y1; i <= y2; i++)
  {
    uchar *S1_data = S1.ptr<uchar>(i);
    uchar *Si1_data = Si1.ptr<uchar>(i);
    uchar *Si2_data = Si2.ptr<uchar>(i);


    for (int j = x1; j <= x2; j++)
    {
      sum2_i = sum2_i - S1_data[j] * Si1_data[j] + S1_data[j] * Si2_data[j];
      sum3_i = sum3_i - Si1_data[j] * Si1_data[j] + Si2_data[j] * Si2_data[j];
    }
  }
  //计算NCC的倒数作为目标函数值
  double cc2 = sqrt(sum1*sum3_i) / (sum2_i + 0.0000001);


  return cc2;
}

整体图像FFD形变代码：

void Bspline_Ffd(Mat srcimg, Mat &dstimg, int row_block_num, int col_block_num, Mat grid_points)
{
  dstimg.create(srcimg.size(), srcimg.type());


  float delta_x = srcimg.cols*1.0 / col_block_num;
  float delta_y = srcimg.rows*1.0 / row_block_num;
  int grid_rows = row_block_num + BPLINE_BOARD_SIZE;
  int grid_cols = col_block_num + BPLINE_BOARD_SIZE;
  int grid_size = grid_rows*grid_cols;


  float pX[4], pY[4];


  for (int y = 0; y < srcimg.rows; y++)   //B_spline 变形 
  {
    for (int x = 0; x < srcimg.cols; x++)
    {
      float y_block = y / delta_y;
      float x_block = x / delta_x;
      int i = floor(y_block);
      int j = floor(x_block);
      float u = x_block - j;
      float v = y_block - i;


      //使用基函数计算权重系数
      pX[0] = (1 - u*u*u + 3 * u*u - 3 * u) / 6.0;
      pX[1] = (4 + 3 * u*u*u - 6 * u*u) / 6.0;
      pX[2] = (1 - 3 * u*u*u + 3 * u*u + 3 * u) / 6.0;
      pX[3] = u*u*u / 6.0;
      pY[0] = (1 - v*v*v + 3 * v*v - 3 * v) / 6.0;
      pY[1] = (4 + 3 * v*v*v - 6 * v*v) / 6.0;
      pY[2] = (1 - 3 * v*v*v + 3 * v*v + 3 * v) / 6.0;
      pY[3] = v*v*v / 6.0;


      float Tx = 0;
      float Ty = 0;
      for (int m = 0; m < 4; m++)
      {
        for (int n = 0; n < 4; n++)
        {
          int control_point_x = j + n;
          int control_point_y = i + m;




          float temp = pY[m] * pX[n];
          Tx += temp*grid_points.at<float>(0, control_point_y*grid_cols + control_point_x);    //x
          Ty += temp*grid_points.at<float>(0, control_point_y*grid_cols + control_point_x + grid_size);    //y
        }
      }


      float src_x = x + Tx;
      float src_y = y + Ty;
      int x1 = cvFloor(src_x);
      int y1 = cvFloor(src_y);
      if (x1 < 1 || x1 >= srcimg.cols - 1 || y1 < 1 || y1 >= srcimg.rows - 1)//越界
      {
        dstimg.at<uchar>(y, x) = 0;
      }
      else
      {
        //双线性插值
        int x2 = x1 + 1;
        int y2 = y1 + 1;
        uchar pointa = srcimg.at<uchar>(y1, x1);
        uchar pointb = srcimg.at<uchar>(y1, x2);
        uchar pointc = srcimg.at<uchar>(y2, x1);
        uchar pointd = srcimg.at<uchar>(y2, x2);
        uchar gray = (uchar)((x2 - src_x)*(y2 - src_y)*pointa - (x1 - src_x)*(y2 - src_y)*pointb - (x2 - src_x)*(y1 - src_y)*pointc + (x1 - src_x)*(y1 - src_y)*pointd);
        dstimg.at<uchar>(y, x) = gray;
      }
    }
  }
}

计算I2的ΔI区域FFD形变图像代码，其中的(x1,y1)、(x2,y2)分别为ΔI区域的左上角、右下角坐标，由以上函数cal_rect_area得到。函数Bspline_Ffd_area与以上的函数Bspline_Ffd的主要区别在于，前者仅计算部分区域的形变，后者计算整张图像的形变：

void Bspline_Ffd_area(Mat srcimg, Mat &dstimg, int row_block_num, int col_block_num, Mat grid_points, int x1, int y1, int x2, int y2)
{
  dstimg = Mat::zeros(srcimg.size(), CV_8UC1);


  float delta_x = srcimg.cols*1.0 / col_block_num;
  float delta_y = srcimg.rows*1.0 / row_block_num;
  int grid_rows = row_block_num + BPLINE_BOARD_SIZE;
  int grid_cols = col_block_num + BPLINE_BOARD_SIZE;
  int grid_size = grid_rows*grid_cols;


  float pX[4], pY[4];
  float *p_grid = grid_points.ptr<float>(0);


  for (int y = y1; y <= y2; y++)   //B_spline变形，只对矩形区域变形
  {
    float y_block = y / delta_y;
    int i = floor(y_block);
    float v = y_block - i;
    float v2 = v*v;
    float v3 = v2*v;
    pY[0] = (1 - v3 + 3 * v2 - 3 * v) / 6.0;  //使用基函数计算权重系数
    pY[1] = (4 + 3 * v3 - 6 * v2) / 6.0;
    pY[2] = (1 - 3 * v3 + 3 * v2 + 3 * v) / 6.0;
    pY[3] = v3 / 6.0;


    uchar *p_dst = dstimg.ptr<uchar>(y);


    for (int x = x1; x <= x2; x++)
    {
      float x_block = x / delta_x;
      int j = floor(x_block);
      float u = x_block - j;
      float u2 = u*u;
      float u3 = u2*u;
      pX[0] = (1 - u3 + 3 * u2 - 3 * u) / 6.0;   //使用基函数计算权重系数
      pX[1] = (4 + 3 * u3 - 6 * u2) / 6.0;
      pX[2] = (1 - 3 * u3 + 3 * u2 + 3 * u) / 6.0;
      pX[3] = u3 / 6.0;


      float Tx = 0;
      float Ty = 0;
      for (int m = 0; m < 4; m++)
      {
        for (int n = 0; n < 4; n++)
        {
          int control_point_x = j + n;
          int control_point_y = i + m;


          float temp = pY[m] * pX[n];
          Tx += temp*p_grid[control_point_y*grid_cols + control_point_x];    //x
          Ty += temp*p_grid[control_point_y*grid_cols + control_point_x + grid_size];    //y                                      
        }
      }


      float src_x = x + Tx;
      float src_y = y + Ty;
      int x1 = cvFloor(src_x);
      int y1 = cvFloor(src_y);
      if (x1 < 1 || x1 >= srcimg.cols - 1 || y1 < 1 || y1 >= srcimg.rows - 1)//越界
      {
        p_dst[x] = 0;
      }
      else
      {
        int x2 = x1 + 1;   //双线性插值
        int y2 = y1 + 1;
        uchar pointa = srcimg.at<uchar>(y1, x1);
        uchar pointb = srcimg.at<uchar>(y1, x2);
        uchar pointc = srcimg.at<uchar>(y2, x1);
        uchar pointd = srcimg.at<uchar>(y2, x2);
        uchar gray = (uchar)((x2 - src_x)*(y2 - src_y)*pointa - (x1 - src_x)*(y2 - src_y)*pointb - (x2 - src_x)*(y1 - src_y)*pointc + (x1 - src_x)*(y1 - src_y)*pointd);
        p_dst[x] = gray;
      }
    }
  }
}

梯度计算代码实现：

void cal_gradient_area(Mat S1, Mat Si, int row_block_num, int col_block_num, Mat grid_points, Mat &gradient)
{
  float EPS = 0.1;
  int grid_size = grid_points.cols / 2;
  int x1, y1, x2, y2;
  double cc1, cc2;


  gradient.create(grid_points.size(), CV_32FC1);


  double sum1 = 0.0, sum2 = 0.0, sum3 = 0.0;
  Mat Si_ffd1, Si_ffd2;
  //计算I1
  Bspline_Ffd(Si, Si_ffd1, row_block_num, col_block_num, grid_points);
  //计算1.0/NCC(A,I1)
  cc1 = cal_cc1(S1, Si_ffd1, sum1, sum2, sum3);


  Mat grid_p = grid_points.clone();
  for (int i = 0; i < grid_size; i++)
  {
    //获取I1、I2区别区域的左上角、右下角坐标
    cal_rect_area(i, S1.rows, S1.cols, row_block_num, col_block_num, x1, y1, x2, y2);
    //改变一个控制参数的值
    grid_p.at<float>(0, i) += EPS;
    //计算区别区域的形变图像
    Bspline_Ffd_area(Si, Si_ffd2, row_block_num, col_block_num, grid_p, x1, y1, x2, y2);
    //快速计算1.0/NCC(A,I2)
    cc2 = cal_cc2(S1, Si_ffd1, Si_ffd2, x1, y1, x2, y2, sum1, sum2, sum3);
    grid_p.at<float>(0, i) -= EPS;
    //计算控制点i的x控制参数的梯度
    gradient.at<float>(0, i) = (cc2 - cc1) / EPS;


    //计算控制点i的y控制参数的梯度，原理与以上计算x控制参数梯度一样
    grid_p.at<float>(0, i + grid_size) += EPS;
    Bspline_Ffd_area(Si, Si_ffd2, row_block_num, col_block_num, grid_p, x1, y1, x2, y2);
    cc2 = cal_cc2(S1, Si_ffd1, Si_ffd2, x1, y1, x2, y2, sum1, sum2, sum3);
    grid_p.at<float>(0, i + grid_size) -= EPS;
    gradient.at<float>(0, i + grid_size) = (cc2 - cc1) / EPS;
  }
}

加速梯度计算之后的梯度下降配准代码：

int bpline_match_area(Mat S1, Mat Si, Mat &M, int row_block_num, int col_block_num, Mat &grid_points, int max_iter)
{
  Mat gradient;
  Mat pre_grid_points;
  double e = 0.000005;//定义迭代精度
  float ret1 = 0.0;
  float ret2 = 0.0;
  int cnt = 0;
  float alpha = 8000000;


  cal_gradient_area(S1, Si, row_block_num, col_block_num, grid_points, gradient);   //求梯度
  int out_cnt = 0;


  Mat pre_gradient = Mat::zeros(gradient.size(), CV_32FC1);


  while (cnt < max_iter)
  {
    pre_grid_points = grid_points.clone();
    update_grid_points(grid_points, gradient, alpha);  //更新输入参数


    ret1 = F_fun_bpline(S1, Si, row_block_num, col_block_num, pre_grid_points);
    ret2 = F_fun_bpline(S1, Si, row_block_num, col_block_num, grid_points);


    if (ret2 > ret1)  //如果当前轮迭代的目标函数值大于上一轮的函数值，则减小步长并重新计算梯度、重新更新参数
    {
      alpha *= 0.8;
      grid_points = pre_grid_points.clone();
      continue;
    }


    cout << "f=" << ret2 << ", alpha=" << alpha << endl;


    if (abs(ret2 - ret1) < e)
    {
      out_cnt++;
      if (out_cnt >= 4)   //如果连续4次目标函数值不改变，则认为求到了最优解，停止迭代
      {
        break;
      }
    }
    else
    {
      out_cnt = 0;
    }


    gradient.copyTo(pre_gradient);
    cal_gradient_area(S1, Si, row_block_num, col_block_num, grid_points, gradient);  //求梯度


    if (norm(gradient, NORM_L2) <= norm(pre_gradient, NORM_L2))  //如果梯度相比上一次迭代有所下降，则增大步长
      alpha *= 2;


    cnt++;
  }


  Bspline_Ffd(Si, M, row_block_num, col_block_num, grid_points);


  return -1;
}

加速梯度计算之后，使用23*23的FFD网格对472*496大小的Lena图像进行配准，每轮迭代耗时300~400 ms，相对于加速前每轮迭代耗时11 s左右，加速效果还是相当明显的。

好了本文我们就讲到这里，欢迎关注本公众号，接下来的更新更精彩~