目录
1. 前言
Hash函数不是计算理论的中基本概念,计算理论中只有单向函数的说法。所谓的单向函数,是一个复杂的定义,严格的定义要参考理论或者密码学方面的书籍。用“人类”的语言描述单向函数就是:如果某个函数在给定输入的时候,很容易计算出其结果来;而当给定结果的时候,很难计算出输入来,这就是单向函数。各种加密函数都可以被认为是单向函数的逼近。Hash函数(或者成为散列函数)也可以看成是单向函数的一个逼近。即它接近于满足单向函数的定义。
Hash函数还有更通俗的理解方式,即它代表的是一种关于数据的压缩映射。实际中的Hash函数是指把一个大范围映射到一个小范围。把大范围映射到一个小范围的目的往往是为了节省空间,使得数据容易保存。除此以外,Hash函数往往应用于查找上。所以,在考虑使用Hash函数之前,需要明白它的几个限制:
(1) Hash的主要原理就是把大范围映射到小范围;所以,你输入的实际值的个数必须和小范围相当或者比它更小。不然冲突就会很多。
(2) 由于Hash逼近单向函数;所以,你可以用它来对数据进行加密。
(3) 不同的应用对Hash函数有着不同的要求;比如,用于加密的Hash函数主要考虑它和单向函数的差距,而用于查找的Hash函数主要考虑它映射到小范围的冲突率。
Hash函数应用的主要对象是数组(比如,字符串),而其目标一般是一个int类型。
一般的说,Hash函数可以简单的划分为如下几类:
1. 加法Hash;
2. 位运算Hash;
3. 乘法Hash;
4. 除法Hash;
5. 查表Hash;
6. 混合Hash;
本文主要讨论关于哈希概率的计算及其简易python仿真。
2. 生日问题
从数学上来说,哈希冲突概率问题其实是一个更通俗的所谓的“生日问题(birthday problem)”的一般化。
生日问题:假定人群中生日在一年的365天中分配是符合均一分布(uniform distribution)的(换句话说,1年的365天中每天出生的人数统计意义上是相等的)。在k个人的聚会中,至少有2个人生日是同一天的概率有多大?进一步,至少有2个人生日是同一天的概率超过50%的最小的N是多少?
这个问题的结果有些反直觉,所以如果不经过严格的计算,很难猜到哪怕是大致接近的答案。以下来讨论如何计算这个概率。
我们要计算的是至少有两个人发生生日冲突的概率,但是直接计算这个不容易。作为一个概率计算中的常用技巧,我们考虑“至少有两个人发生生日冲突”这个事件的补事件--即任何两人之间都不发生生日冲突--的概率。
以下的描述中用生日冲突表示两个人生日为同一天。
考虑第1个人,很显然TA不会与任何人生日冲突
考虑第2个人,TA与第一个人不发生生日冲突的概率为很显然为
考虑第3个人,TA与前两个人发生生日冲突的概率为很显然为
...
考虑第k个人,TA与前(k-1)个人发生生日冲突的概率为很显然为
因此k个人不发生生日冲突的概率为:
因此,最少有两个人的生日恰好为同一天的概率则是:
3. 哈希冲突问题
假定哈希函数在将数据从一个大的空间(记为输入空间)压缩映射到一个小的空间(记为目标空间)时,是遵从均一分布的话,那么哈希冲突(任意两个输入空间的数据映射到目标空间中的相同数据)的概率问题,其实就是以上生日问题中发生生日冲突的概率问题的一般化问题。只不过目标空间的大小从生日问题中的365变为一般化的N。
即目标空间大小为N时的一般化的哈希冲突概率为:
在N非常大的时候,计算上式右边的第2部分会比较慢,所幸的是,这个式子可以很好地进行如下近似:
4. 简易python仿真
# -*- coding: utf-8 -*-
"""
Created on Mon Nov 21 13:44:55 2022
@author: chenxy
ref: https://preshing.com/20110504/hash-collision-probabilities/
"""
import math
import numpy as np
import matplotlib.pyplot as plt
import time
def probCollision(N,k):
probCollision = 1.0
for j in range(k):
probCollision = probCollision * (N - j) / N
return 1 - probCollision
def probCollisionApproximation(N,k):
# return 1 - math.exp(-0.5 * k * (k - 1) / N)
return 1 - np.exp(-0.5 * k * (k - 1) / N)
if __name__ == '__main__':
tstart=time.time()
Pcollision = [0]
for k in range(1,100):
Pcollision.append(probCollision(365, k))
print('k = {0}, Pcollision[k] = {1}'.format(k,Pcollision[k]))
tstop=time.time()
print('Total elapsed time = {0} seconds'.format(tstop-tstart))
tstart=time.time()
Pcollision2 = [0]
for k in range(1,100):
Pcollision2.append(probCollisionApproximation(365, k))
print('k = {0}, Pcollision2[k] = {1}'.format(k,Pcollision2[k]))
tstop=time.time()
print('Total elapsed time = {0} seconds'.format(tstop-tstart))
plt.plot(Pcollision)
plt.plot(Pcollision2)运行结果如下:
。。。
k = 17, Pcollision2[k] = 0.31106113346867104
k = 18, Pcollision2[k] = 0.34241291970846444
k = 19, Pcollision2[k] = 0.37405523755741676
k = 20, Pcollision2[k] = 0.40580512747932584
k = 21, Pcollision2[k] = 0.4374878053458634
k = 22, Pcollision2[k] = 0.4689381107801478
k = 23, Pcollision2[k] = 0.5000017521827107
k = 24, Pcollision2[k] = 0.5305363394090516
k = 25, Pcollision2[k] = 0.5604121995072768。。。
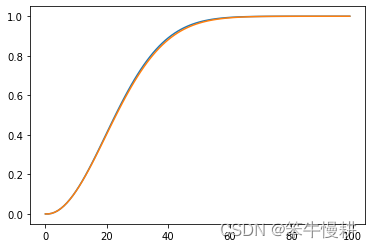
由以上仿真结果可以看出:
(1)上一节所说的近似方法的准确度非常高,两种方法计算结果从图上看几乎一致
(2)生日冲突概率在23个人时就超过50%了!这意味着23个人聚会时,至少有两个人生日为同一天的概率就超过50%了。想一想一年有365天,区区23个人凑在一起就有超过一半的概率会出现某两个人生日为同一天,是不是有点神奇?
进一步,对任意N进行仿真,我们可以发现,对任意N来说,冲突概率曲线都是以上这个形状。这意味着,冲突概率其实可以表达为归一化数(k/N)的函数,与具体的k和N其实是无关的。
5. 从另一个角度看哈希冲突概率
本节从另一个角度来考察哈希冲突概率。
给定一个目标空间的大小N,随机地进行从输入空间进行数据采样并将其映射到目标空间,需要多少个输入数据才能将目标空间填满呢?目标空间的填充率与冲突概率之间是什么关系呢?
以下针对这个问题做一个蒙特卡洛仿真。代码如下:
# -*- coding: utf-8 -*-
"""
Created on Sat Nov 26 10:04:08 2022
@author: chenxy
"""
# generate random 160 bits key
import numpy as np
import random
from collections import defaultdict
import time
import matplotlib.pyplot as plt
def key160_gen() -> int:
"""
Generate one random 160 bits key
Returns
-------
int
160 bits key.
"""
return random.randint(0,2**160-1)
def hash_sim(cam_depth):
hcam = np.zeros((cam_depth,))
key_cnt = 0
query_ok_cnt = 0
collision_cnt = 0
camfill_cnt = 0
while 1:
key_cnt += 1
key = key160_gen()
key_hash = hash(key) %(cam_depth)
# print('key = {0}, key_hash = {1}'.format(key,key_hash))
if key == hcam[key_hash]:
query_ok_cnt += 1
else:
if hcam[key_hash]==0:
camfill_cnt += 1
else:
collision_cnt += 1
hcam[key_hash] = key
# if key_cnt %4096 == 0:
# print('key_cnt = {0}, camfill_cnt = {1}'.format(key_cnt,camfill_cnt))
if camfill_cnt == cam_depth:
# print('CAM has been filled to full, with {0} key operation'.format(key_cnt))
break
return key_cnt, collision_cnt
rslt = []
for k in range(10,20):
tStart = time.time()
cam_depth = 2**k
key_cnt,collision_cnt = hash_sim(2**k)
tElapsed = time.time() - tStart
print('cam_depth={0}, key_cnt={1}, collision_prob={2:4.3f}, tCost={3:3.2f}(sec)'.format(cam_depth,key_cnt,collision_cnt/key_cnt,tElapsed))
rslt.append([cam_depth,key_cnt])
rslt = np.array(rslt)
plt.plot(rslt[:,0],rslt[:,1])
运行结果如下:
cam_depth=1024, key_cnt=6010, collision_prob=0.830, tCost=0.07(sec)
cam_depth=2048, key_cnt=16034, collision_prob=0.872, tCost=0.17(sec)
cam_depth=4096, key_cnt=30434, collision_prob=0.865, tCost=0.30(sec)
cam_depth=8192, key_cnt=89687, collision_prob=0.909, tCost=0.87(sec)
cam_depth=16384, key_cnt=149980, collision_prob=0.891, tCost=1.15(sec)
cam_depth=32768, key_cnt=314527, collision_prob=0.896, tCost=2.38(sec)
cam_depth=65536, key_cnt=866673, collision_prob=0.924, tCost=6.48(sec)
cam_depth=131072, key_cnt=1518369, collision_prob=0.914, tCost=11.08(sec)
cam_depth=262144, key_cnt=3657451, collision_prob=0.928, tCost=26.70(sec)
cam_depth=524288, key_cnt=6648966, collision_prob=0.921, tCost=48.48(sec)
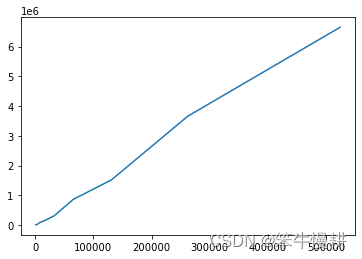
以上仿真结果表明,要让哈希表以满填充状态工作的话,哈希冲突概率大概为90%左右,也就是说放入哈希表的操作大概每10次会发生9次冲突!基于哈希表的应用中最重要的问题就是如何解决哈希冲突的问题。
参考文献: