堆 堆排序 TopK问题

一，堆的相关函数接口实现

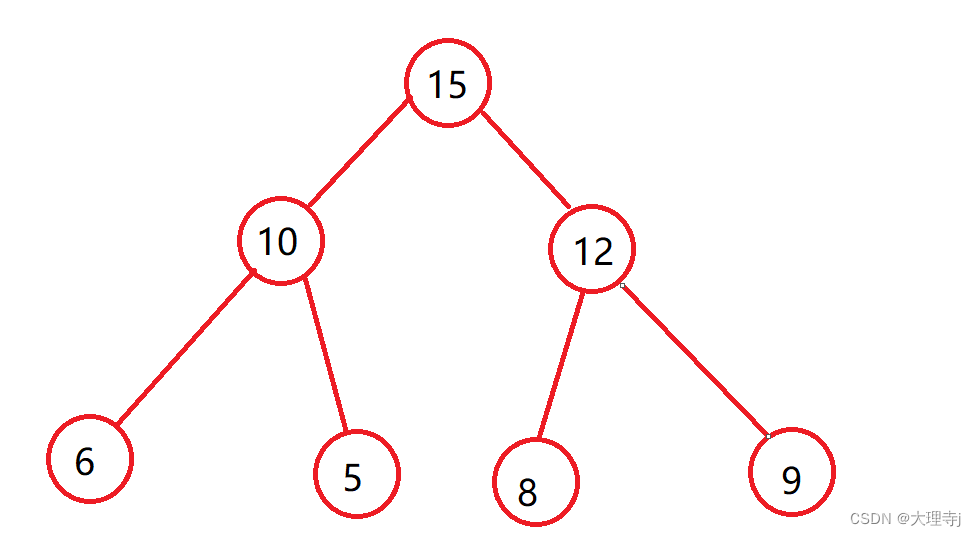
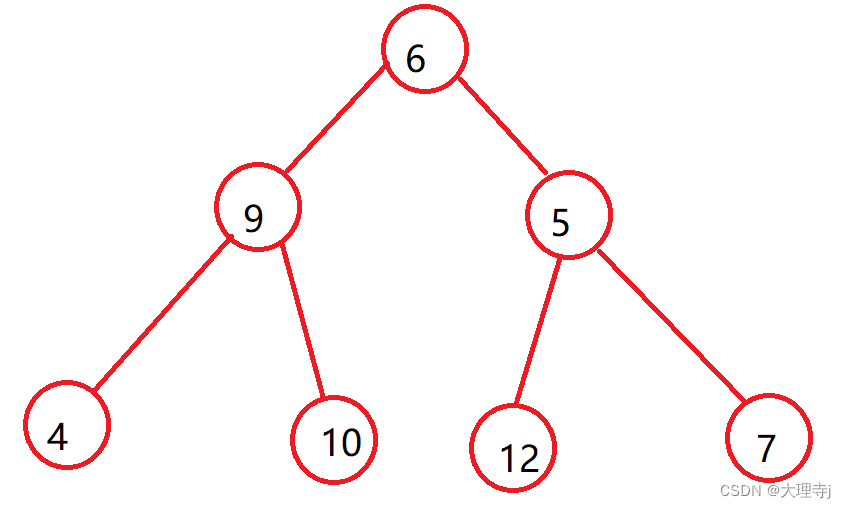
堆是一颗完全二叉树，分为大堆和小堆两种结构
大堆：任何一个父节点都大于等于子节点，上图就是一个大堆
小堆：任何一个父节点都小于等于子节点
在顺序表中父节点与子节点的下标存在哪些关系呢？
leftchild=parent * 2+1
rightchild=parent * 2+2
那么，同样可以得到
父亲结点的下表就是（儿子结点下标-1）/2
主要采用顺序表来存储堆这个数据结构
主要完成以下的函数接口

#pragma once

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>

typedef int HPDataType;
typedef struct Heap
{
    
    
	HPDataType* a;
	int capcity;
	int size;
}Heap;

void HeapInit(Heap* php);
void HeapDestroy(Heap* php);
void HeapPush(Heap* php, HPDataType x);
void HeapPop(Heap* php);
HPDataType HeapTop(Heap* php);
bool HeapEmpty(Heap* php);
int HeapSize(Heap* php);
void  HeapCreate(Heap* php,HPDataType* a, int size);
void AdjustDown(HPDataType* a, int size, int parent);
void AdjustUp(HPDataType* a, int child);

1，堆的初始化

初始化很简单就是把用来存储堆的顺序表进行初始化

void HeapInit(Heap* php)
{
    
    
	assert(php);
	php->a = NULL;
	php->capcity = 0;
	php->size = 0;
}

2，堆的销毁

void HeapDestroy(Heap* php)
{
    
    
	assert(php);
	free(php->a);
	php->a = NULL;
	php->capcity = 0;
	php->size = 0;
}

3，插入

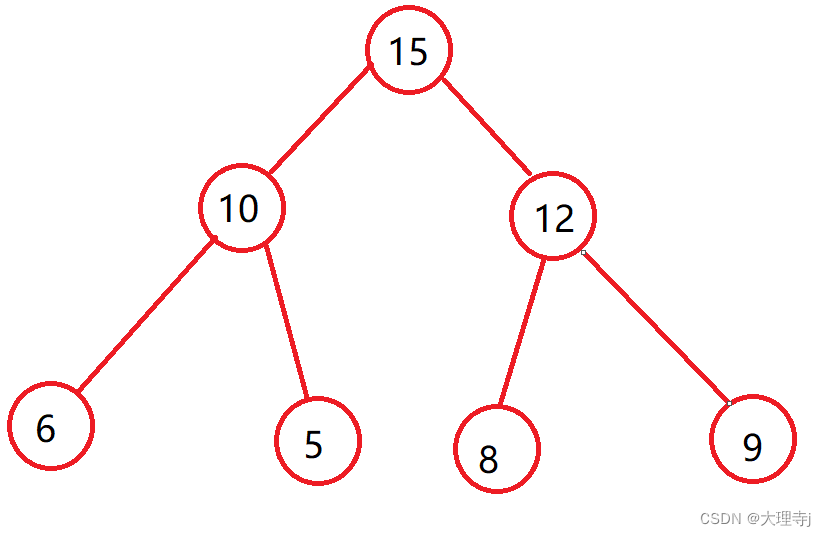
现在要插入一个结点，那么肯定是会链接到6的左子树的位置。
如果，插入结点的值是小于6的值，那么不会影响堆的结构，仍然是一个大堆。
如果，插入节点的值是大于6的值，那么此时就会影响堆的结构，使起其不是一个大堆，所以我们就到对这个结点进行向上调整。并且调整过程中只会改变此要调整的结点与其父节点的相对位置，直至符合大堆的结构为止。

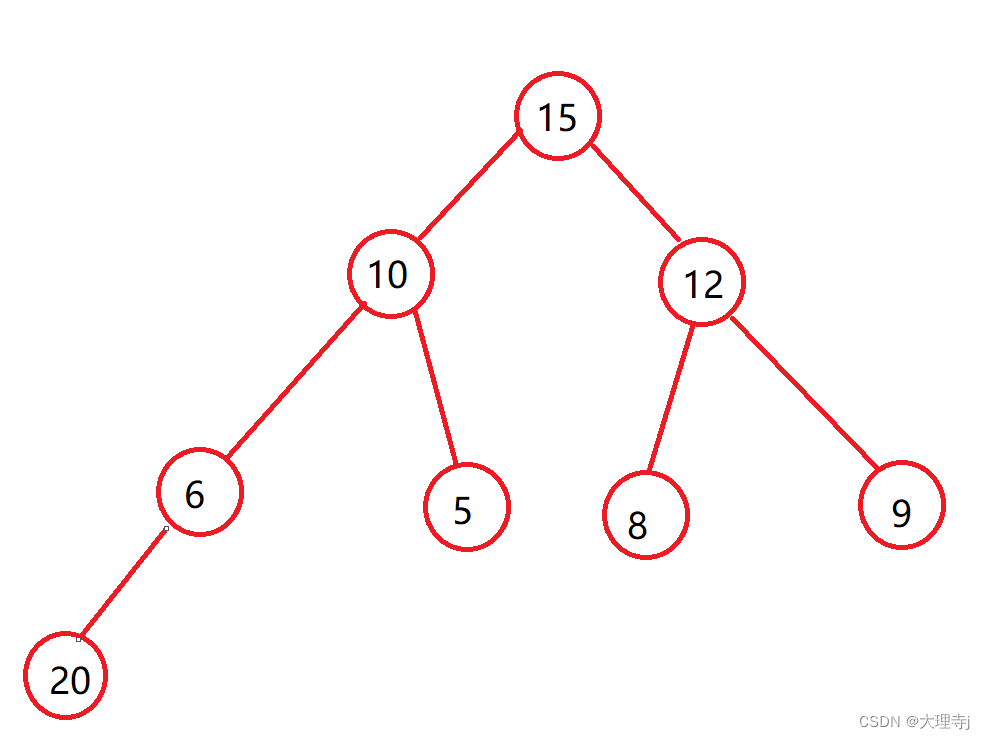
我们先用图示来展现以下调整的过程：依次向上调整

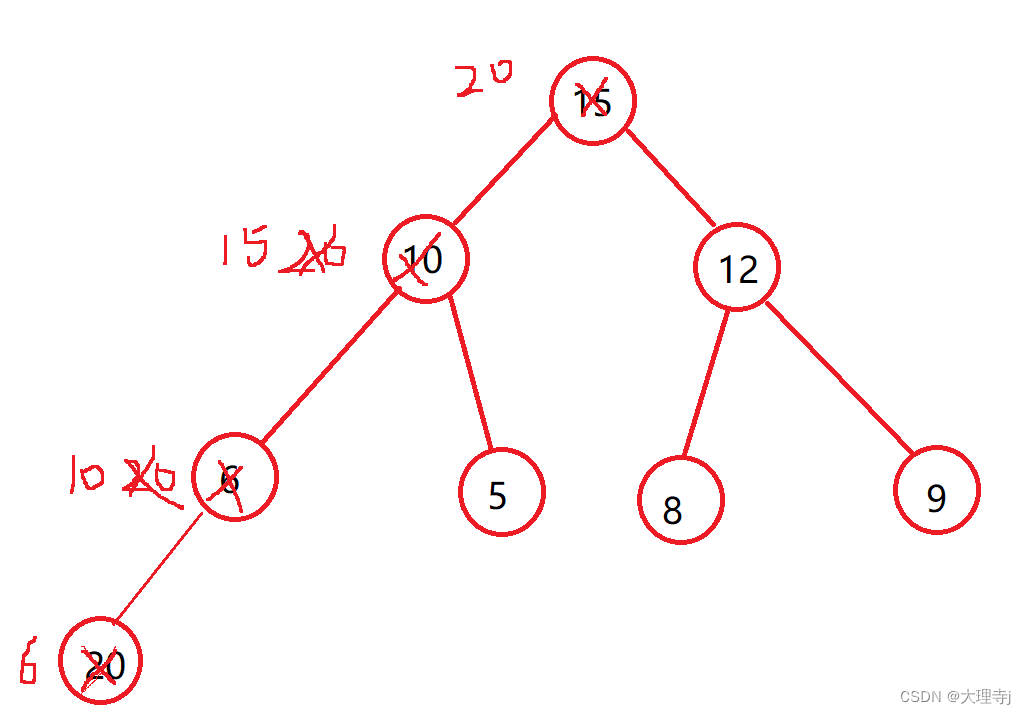
插入之前还要判断是否需要扩容。

void HeapPush(Heap* php, HPDataType x)
{
    
    
	assert(php);
	if (php->capcity == php->size)
	{
    
    
		int newcapcity = (php->capcity == 0 ? 4 : php->capcity * 2);
		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapcity);
		if (!tmp)
		{
    
    
			perror("realloc fail");
			exit(-1);
		}
		php->a = tmp;
		php->capcity = newcapcity;
	}
	php->a[php->size] = x;
	php->size++;
	AdjustUp(php->a, php->size - 1);
}

4，向上调整

void AdjustUp(HPDataType* a, int child)
{
    
    
	int parent = (child - 1) / 2;
	while (child > 0)
	{
    
    
		if (a[child] > a[parent])
		{
    
    
			swep(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
    
    
			break;
		}
	}
}

5，删除

删除结点时，通常删除的都是堆顶结点，因为如果时大堆那么堆顶数据就是最大的，反之就是最小的，删除其他结点没有什么意义。
删除时也有技巧，如果我们直接把后面的数据向前移动覆盖掉第一个数据，那么整个堆将变成无序的，所以我们采用这样的方式：
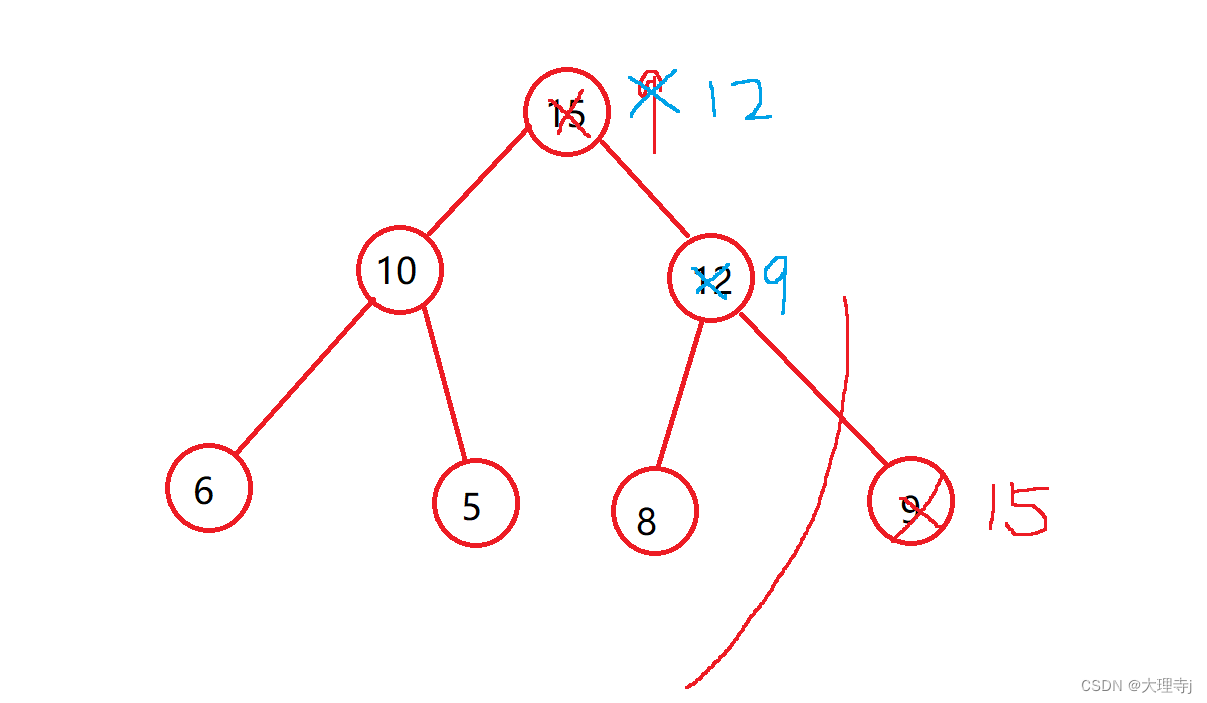
先将堆顶元素与最后一个元素交换，然后size–
此时，堆顶的左子树和右子树一定还是一个大堆没有被破坏，所以，我们就需要向下调整，与向上调整类似，直至成为大堆结构为止。

向下调整时要特别注意，如果父节点比子节点小的话，那么与父节点交换的一定是左右子节点中较大的那一个

void HeapPop(Heap* php)
{
    
    
	assert(php);
	assert(!HeapEmpty(php));
	//首尾交换
	swep(&php->a[0], &php->a[php->size - 1]);
	php->size--;
	//向下调整
	AdjustDown(php->a, php->size, 0);
}

6，向下调整

void AdjustDown(HPDataType* a, int size, int parent)
{
    
    
	int child = parent * 2 + 1;
	while (child < size)
	{
    
    
		//如果右子树大于左子树那么孩子结点就选右子树
		if (child + 1 < size && a[child + 1] > a[child])
		{
    
    
			child++;
		}
		if (a[child] > a[parent])
		{
    
    
			swep(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
    
    
			break;
		}
	}
}

7，建堆

上面的建堆模式是逐个插入建堆的，效率比较低
下面我来介绍两种建堆方式，是基于向上调整与向下调整的。

第一种是向上调整建堆
第二种是向下调整建堆

向上调整建堆，基于的是在插入这个数据前原本就是个大堆
给定一个数组，从下标为1开始向上调整（因为只有一个元素时，即是大堆也是小堆），直至最后一个元素。

向下调整建堆，基于的条件是左右字数都是大堆

如上图这种结构，对于6来说左右子树都不是大堆，所以不能从6开始调整，但是我们可以从下往上走，5的左右字数都是大堆，那么先调整5，依次调整9，6。

void  HeapCreate(Heap* php, HPDataType* a, int size)
{
    
    
	assert(php);
	php->a = (HPDataType*)malloc(sizeof(HPDataType) * size);
	if (!php->a)
	{
    
    
		perror("malloc fail");
		exit(-1);
	}
	php->capcity = size;
	php->size = size;
	memcpy(php->a, a, sizeof(HPDataType) * size);
	//向上调整建堆
	/*for (int i = 1; i < size; i++)
	{
		AdjustUp(php->a, i);
	}*/
	//向下调整建堆
	for (int i = (size - 1 - 1) / 2; i >= 0; i--)
	{
    
    
		AdjustDown(php->a, size, i);
	}
}

8，取堆顶

HPDataType HeapTop(Heap* php)
{
    
    
	assert(php);
	assert(!HeapEmpty(php));
	return php->a[0];
}

9，判空

bool HeapEmpty(Heap* php)
{
    
    
	assert(php);
	return php->size == 0;
}

10，堆的大小

int HeapSize(Heap* php)
{
    
    
	assert(php);
	return php->size;
}

二，向上建堆与向下建堆的时间复杂度

上面介绍了两种建堆方式，那我们在使用中采用哪种方式呢？
肯定是选择效率高的那种，所以我们现在来计算以下两种方式的时间复杂度

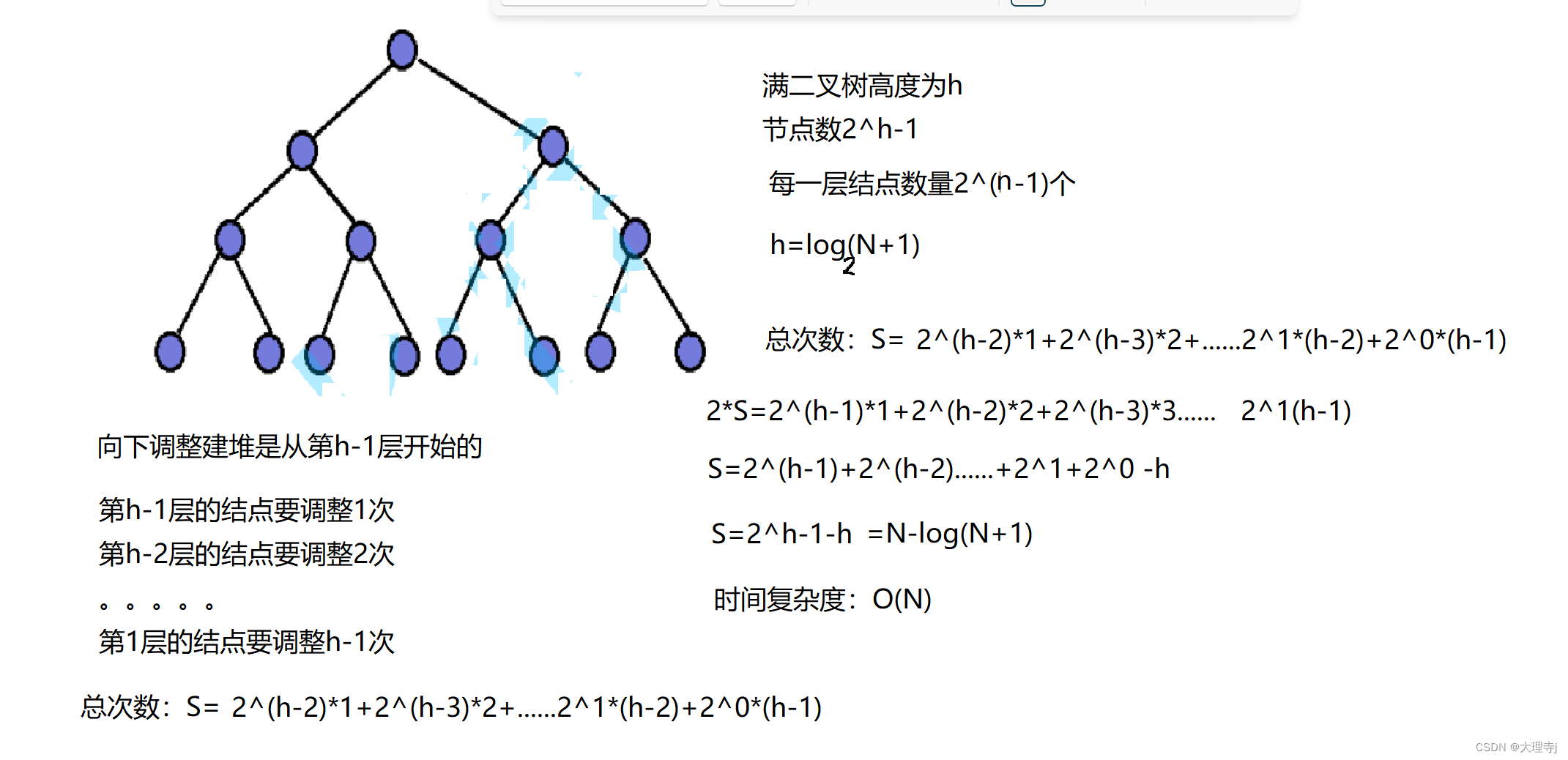
向下调整

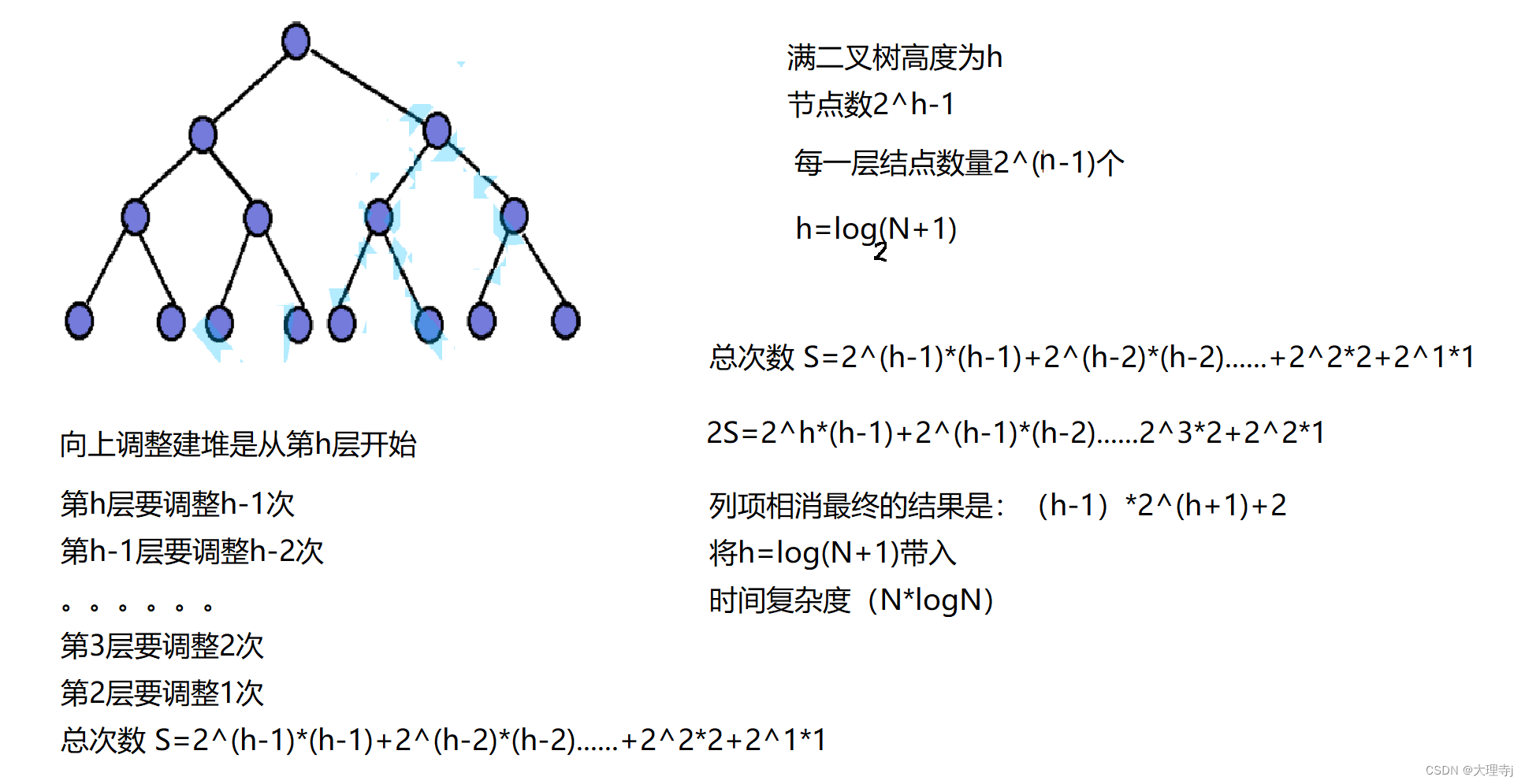
向上调整

可见向下调整建堆要优于向上调整建堆。

三，堆排序

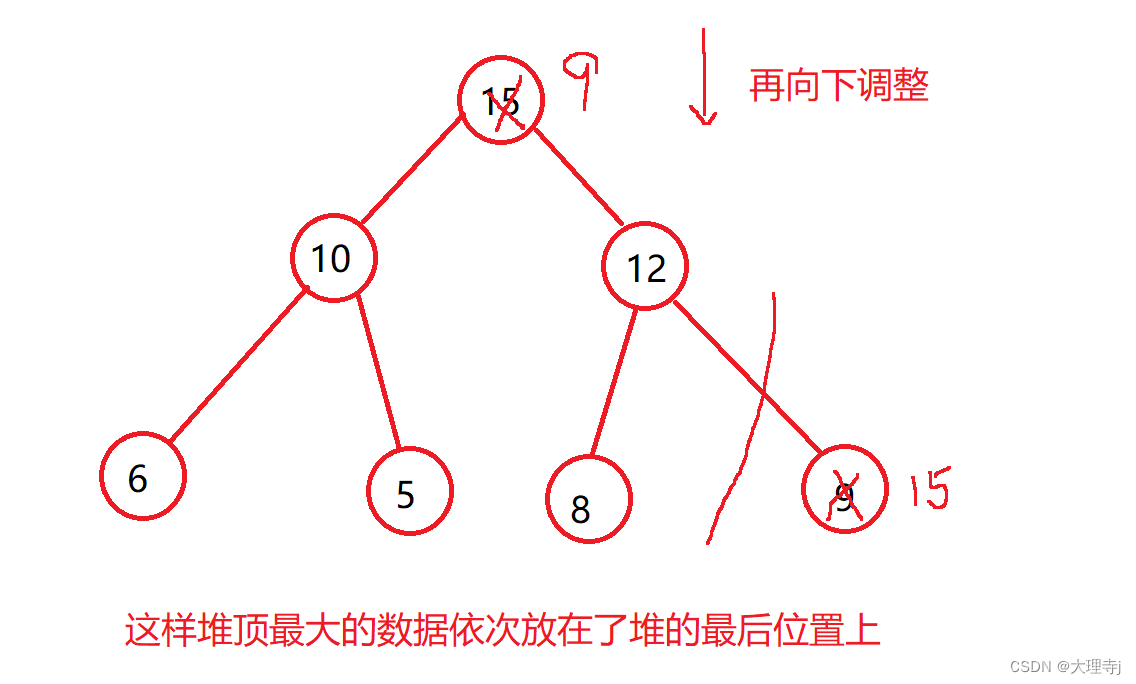
堆排序的思路是根据所给的数组进行向下调整建堆（升序建大堆，降序建小堆）
以升序为例，我们在建堆成功后堆顶元素是数组中最大的数据，将其与堆的最后一个数据交换，这样最大的数据就被放到了最后面，然后size–使堆的数据减少一个，保证后面操作不会影响到前一步选出的最大的数据，然后向下调整建堆再依次操作。

void HeapSort(int* a, int size)
{
    
    
	//升序建大堆
	for (int i = (size - 2) / 2; i >= 0; i--)
	{
    
    
		AdjustDown(a, size, i);
	}
	int end = size - 1;
	while (end > 0)
	{
    
    
		swep(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		end--;
	}
}

堆排序的时间复杂度的计算式类似于向上调整的式子，
时间复杂度：O(N*logN) 空间复杂度O（1）

四，TopK问题

TopK问题的思路有两种：
我们以选出最大的K个数为例
1，将所有数据建立一个大堆，每次取堆顶，再删除堆顶，向下调整。
但是，这种思路的缺点是当所给的数据量巨大，内存放不下的时候，将会无法操作。
2，建立一个K个结点的小堆，由于小堆的堆顶是最小的数据，接下来遍历整个数据只要比堆顶大就进堆，再向下调整，知道遍历完，最大的K个数就全在堆中了。
这种思路就不用担心内存的问题，数据量大可以从文件中读取数据。
所以我来讲解一下这种思路

void TopK(int* a, int size, int k)
{
    
    
	int* minHeap = (int*)malloc(sizeof(int) * k);
	if (!minHeap)
	{
    
    
		perror("malloc fail");
		exit(-1);
	}
	int j = 0;
	for (j = 0; j < k; j++)
	{
    
    
		minHeap[j] = a[j];
	}
	//建k个结点的堆
	for (int i = (k - 2) / 2; i >= 0; i--)
	{
    
    
		AdjustDown(minHeap, k, i);
	}
	for (; j < size; j++)
	{
    
    
		if (a[j] > minHeap[0])
		{
    
    
			minHeap[0] = a[j];
			AdjustDown(minHeap, k, 0);
		}
	}
	for (int i = 0; i < k; i++)
	{
    
    
		printf("%d ", minHeap[i]);
	}
	
}

思路2的时间复杂度：O (N*logK)
思路1的时间复杂度: O (N)