信息论基础：信道模型与信道容量

实际中的信道

信息论是用概率的方法研究信源和信道。前面已经研究了信源的概率模型，现在开始研究信道的概率模型。

首先考虑的是离散信道，它的输入和输出是离散的随机变量。离散信道$Q$是由输入字母表$A_X$、输出字母表$A_Y$和转移概率矩阵$Q_{j|i}=P(y=b_j|x=a_i)$刻画的。如果信道的当前输出只取决于当前输入，则称信道是无记忆的。无记忆信道比较简单，容易分析。

烽火台

古代的烽火台是一种信道。它的输入符号集 A X = { 放火，不放火 } A_X=\{放火，不放火\} AX​={ 放火，不放火}，输出符号集 A Y = { 有火，没有火 } A_Y=\{有火，没有火\} AY​={ 有火，没有火}。
假设转移概率矩阵为
$$Q=\left[\begin{array}{cc}0.9& 0.1\\ 0.1& 0.9\end{array}\right]$$$Q_{1|1}=Q_{2|2}=0.9$表示通信没有出错的概率很高。$Q_{2|1}$和$Q_{1|2}$代表两种错误的概率。$Q_{2|1}=0.1$表示发送端放火了，但由于天气状况不好等原因，接收端没看见。$Q_{1|2}=0.1$表示发送端并没有放火，但被接收端误以为放火了（比如，发送端在吃烧烤）。

电报

前面在介绍信源编码（符号码）的时候，讲过摩尔斯电码。现在讨论摩尔斯电码在信道中传输的问题。点和线是信道的输入和输出符号集。 A X = A Y = { 点，线 } A_X=A_Y=\{点，线\} AX​=AY​={ 点，线}。假设转移概率矩阵为
$$Q=\left[\begin{array}{cc}0.9& 0.1\\ 0.1& 0.9\end{array}\right]$$$Q_{1|1}=Q_{2|2}=0.9$表示通信没有出错的概率很高。$Q_{2|1}$和$Q_{1|2}$代表两种错误的概率。$Q_{2|1}=0.1$表示发报员发送点，而收报员误识为线的概率。$Q_{1|2}=0.1$表示发报员发送线，而收报员误识为点的概率。电报的点和线是由按键时长决定的。如果发报员的按键时长不够准确，或者信道有噪声干扰，收报员是有可能识别错误。

打字机

打字机可以视为一个信道，输入是用户希望打出的字母，输出是打字机实际产生的字母。打字机包括各种文字输入设备，包括古老的打字机、电脑键盘、触摸屏软键盘、新型的打字技术（例如下图中的PrinType指纹打字）。实际的打字不是完美的。用户想打某个字母（A），由于多种原因，实际打出来的是其他字母（A旁边的字母S）。有多种原因可能造成打字出错，例如，手表软键盘的按键太小，手指动作不准确，键盘硬件缺陷。

打字机（或者键盘）信道的输入和输出符号集相同， A X = A Y = { A , B , . . . , Z , − } A_X=A_Y=\{A,B,...,Z,-\} AX​=AY​={ A,B,...,Z,−}。这里$-$代表空格。转移概率矩阵中具体的数值与设备、用户都有关系，这里就不列出具体的矩阵了。不过这种矩阵的基本特征是，对角线元素（不出错的概率）接近于1，除了对角线，每一行都有个别元素数值较大，而其他元素极小或为0。

字符识别器

许多模式识别问题可以视为通信问题。例如，用户用笔填写表格中的手机号，或者对着电话说手机号。用户想要表达的数字是13812345678，但是由于多种原因，系统识别为13802345678。可能出错的原因有多种，用户的写字不规范或者发言不准确，环境噪声太强，识别算法不够理想。

我儿子三岁的时候，我让他写几个2。他写出来的是这样的。在他看来，这都是2。但是让一个字符识别器把这些 符号都能识别为2，是很困难的。

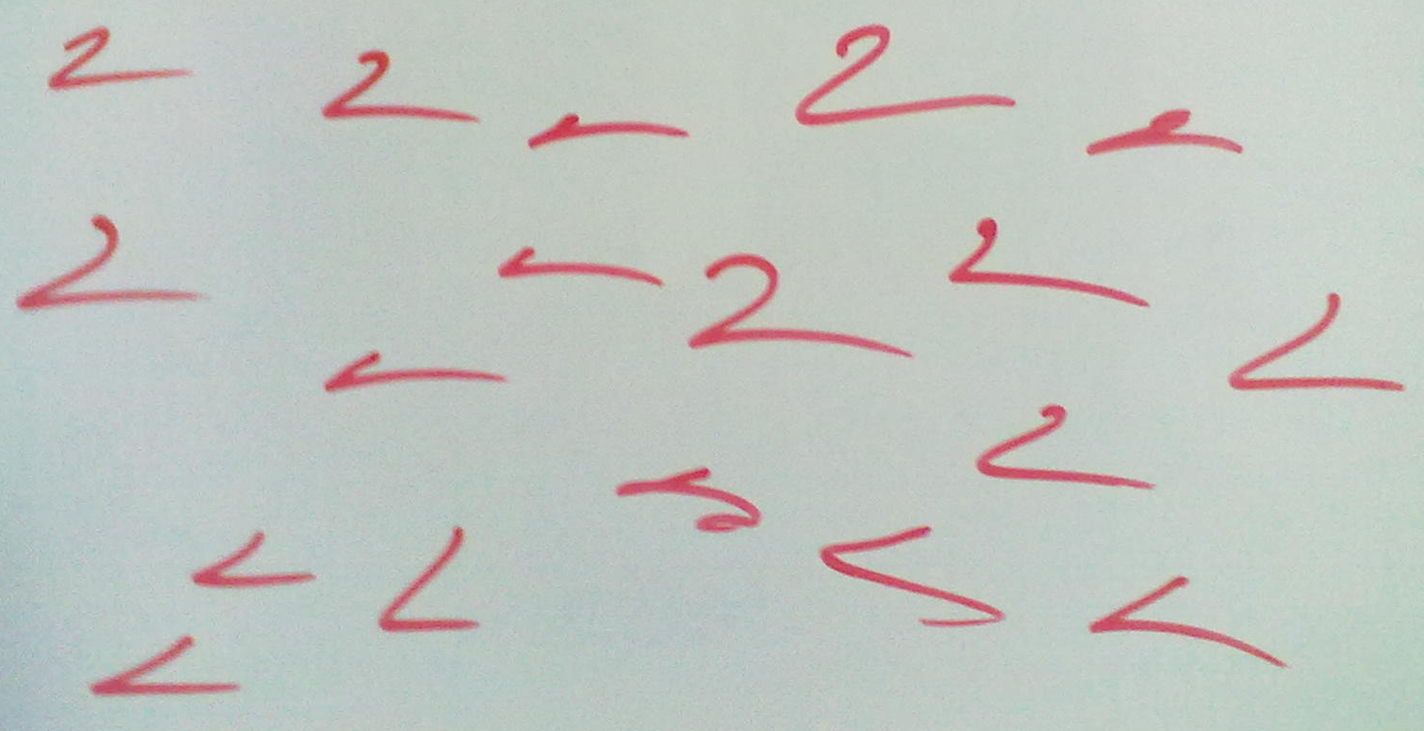
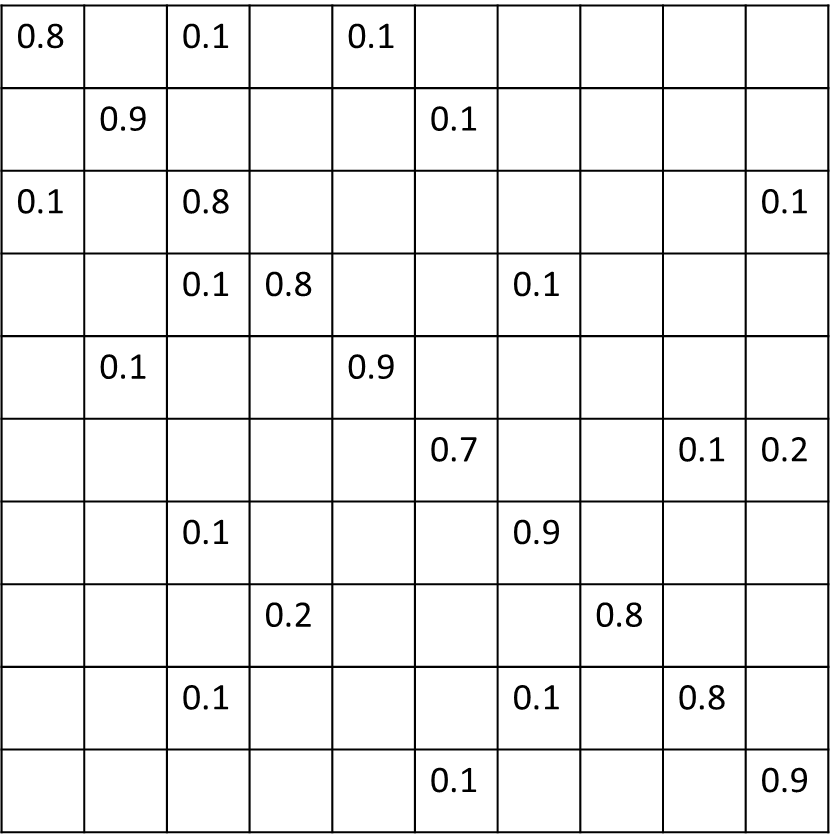
假设某个识别器的转移概率矩阵（在模式识别领域称为混淆矩阵）如下，识别器的输入是行，输出是列。空白处的概率为0。

选择题信道

和字符识别相关的一个信道叫选择题信道。老师让学生做选择题，ABCD四个选项，学生要把选择说出来。
选择题信道的输入和输出符号集相同， A X = A Y = { A , B , C , D } A_X=A_Y=\{A,B,C,D\} AX​=AY​={ A,B,C,D}。
假设转移概率矩阵为
$$Q=\left[\begin{array}{cccc}0.9& 0& 0.1& 0\\ 0& 0.7& 0& 0.3\\ 0.1& 0& 0.9& 0\\ 0& 0.3& 0& 0.7\end{array}\right].$$这样的矩阵是考虑了B和D的读音容易混淆，而A和C容易混淆。

我中学英语课上，老师喜欢叫上课容易睡觉的Q同学做选择题。Q坐在教室的最后一排（座位是按成绩排的），距离老师很远。老师看到Q睡着了，就叫Q做选择题。Q用很小的声音回答B，老师问是B吗，Q说是。过一会，Q又睡着了。老师又叫Q做选择题。Q用很小的声音回答B，老师问是D吗，Q说是。结果命中率50%！

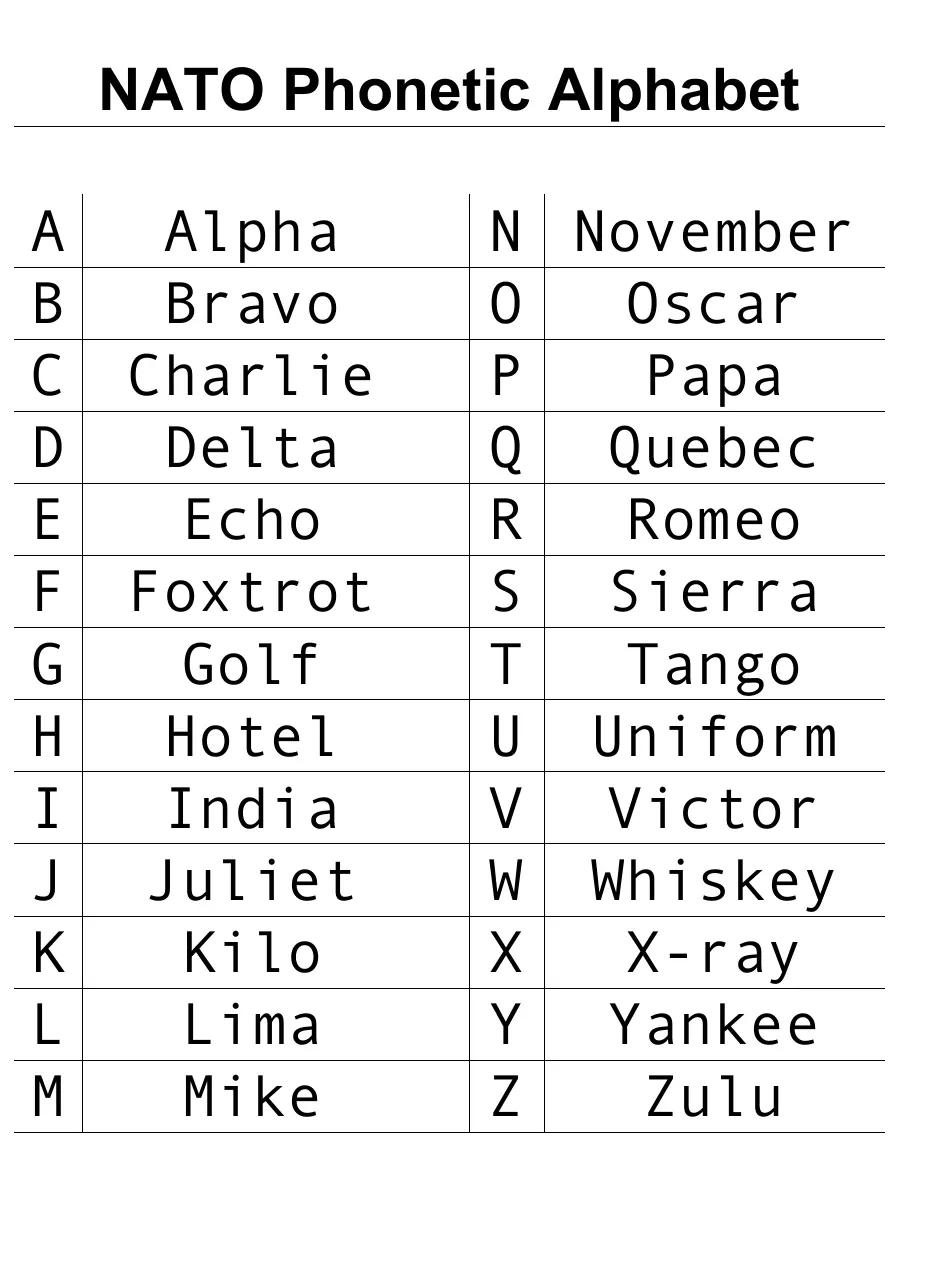
为了降低错误（例如，难以发音的名词、对话双方口音差异大、通话环境很嘈杂），人们发明了音标字母表（spelling alphabet，phonetic alphabet）来代替字母。下面是北约音标字母表（NATO spelling alphabet）。

信道模型

前面从实际生活中列举了一些信道的实际例子。信息论作为一门理论，就像任何一门理论一样，要对具体的现象进行抽象，忽略细节，然后才方便用数学去研究抽象后的模型。下面要介绍一些信道模型，它们都是对实际信道的数学抽象。

• 这是最简单的信道，叫二元无噪声信道。

转移概率矩阵为：

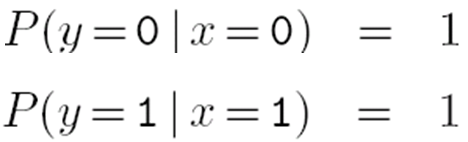
• 无噪声信道是想达到、而又实现不了的理想。BSC是最简单的比较现实的信道模型。

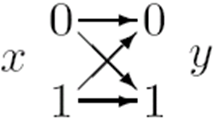
转移概率矩阵为

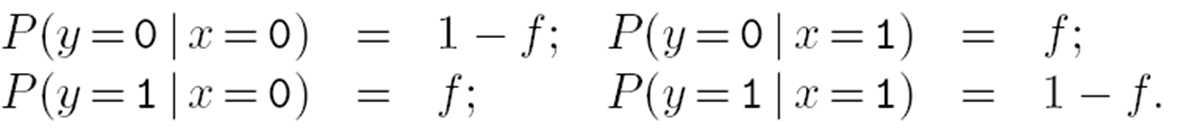
• 二元删除信道BEC。具体例子：发的是方波，幅度>0.6为1，幅<0.4为0，中间为?。

转移概率矩阵为

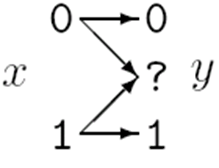
• Z信道。特点：非对称

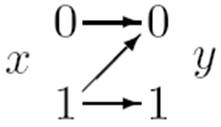
转移概率矩阵为

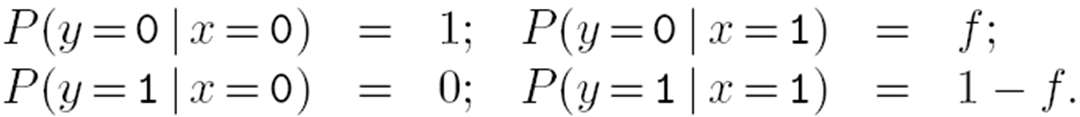
• 噪声打字机信道

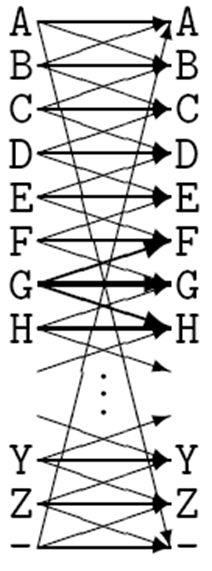
转移概率矩阵为

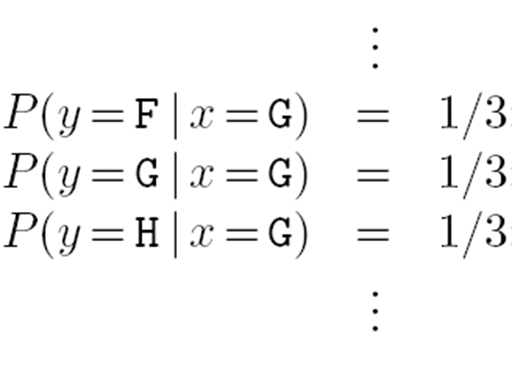
有人可能会质疑打字机信道怎么会这样呢？难度不是相邻的键（asdf）容易混淆啊？信道模型是对具体现象的抽象，不是要代表某一种键盘。

信道容量

上面介绍了一些信道的数学模型。接下来介绍信道的容量。信道容量$C$是每使用信道发送一个符号所能传递的最大信息量。

先看最简单的情况，二元无噪声信道。每使用它发送一个符号所能传递的最大信息量是1比特。一块完美的硬盘，上面标签写的容量是1T字节，那实际容量就是1T字节，1个物理bit的容量就是1个bit。而对于实际的硬盘，需要把校验位算上（这是信道编码产生的），硬盘的1个物理bit的容量不足1个bit。

另一个例子，含32个键的理想打字机信道。每使用它发送一个符号所能传递的最大信息量是${\log }_{2}32=5$比特。

互信息

随机变量$X$和$Y$分别代表信道的输入和输出。虽然收到具体的$y$后，对于$x$仍然不完全确定（因为有噪声），但是信道确实传递了一些信息。多少呢？用互信息$I(X;Y)$度量。

$$I(X;Y)=H(X)-H(X|Y)=H(Y)-H(Y|X)$$

$$H(X|Y)=\sum _{y\in A_Y}P(y)H(X│Y=y)$$
$$H(Y|X)=\sum _{x\in A_X}P(x)H(Y│X=x)$$

链法则证明两种的等价。转移概率矩阵总是P(y|x)，H(Y|X)容易从转移概率矩阵计算。

下面这幅图帮助大家直观看出熵、联和熵、条件熵、互信息之间的关系。通常情况下，条件熵小于熵，信道能传输一定的信息量，但是小于X的信息量（因为噪声的原因）。如何来理解这个互信息作为传输信息量的定义。举两个极端的情况：

• 如果是理想信道，传输的就是X的信息量。条件熵=0。
• 条件独立的时候，传输的信息量0。发送端在发电报呢，接收端不听滴答声，而是掷硬币决定，正面是1，反面是0，完全不管发送端在发什么。这样，接收端和发送端就是完全独立的。信道传输的信息量为0。

对于下面的4个例子，计算互信息。

1. BSC信道，噪声级别f=0.15。输入的概率分布为 P X : { p 0 = 0.9 , p 1 = 0.1 } P_X:\{p_0=0.9, p_1=0.1\} PX​:{ p0​=0.9,p1​=0.1}。
2. BSC信道，噪声级别f=0.15。输入的概率分布为 P X : { p 0 = 0.5 , p 1 = 0.5 } P_X:\{p_0=0.5, p_1=0.5\} PX​:{ p0​=0.5,p1​=0.5}。
3. Z信道，噪声级别f=0.15。输入的概率分布为 P X : { p 0 = 0.9 , p 1 = 0.1 } P_X:\{p_0=0.9, p_1=0.1\} PX​:{ p0​=0.9,p1​=0.1}。
4. Z信道，噪声级别f=0.15。输入的概率分布为 P X : { p 0 = 0.5 , p 1 = 0.5 } P_X:\{p_0=0.5, p_1=0.5\} PX​:{ p0​=0.5,p1​=0.5}。

下表列出了四种情况（两种信道和两种分布）下的互信息。从中可以看出：

• 对于相同的输入分布，Z信道比BSC信道传递更多的信息。
• 对于相同的信道，传递信息量取决于输入分布。.

信道容量为最大互信息

但是，信道容量是信道的特性，应该与输入分布无关。通过选择最优的输入分布，可以使得互信息取得最大值。这个最大值即信道$Q$的容量。
$$C(Q)=\underset{P_X}{\max }I(X;Y).$$
使$I(X;Y)$取到最大值的输入分布称为最优输入分布。

几种信道的容量

• BSC信道：$C(Q)=1-H_2(f)$ bits，最优输入分布为均匀分布。
• BEC信道：$C(Q)=1-f$ bits，最优输入分布为均匀分布。
• 噪声打字机信道：$C(Q)=\log 9$ bits，最优输入分布为均匀分布。
• Z信道：虽然最优输入分布和容量都有显式解，但是很复杂。下面的MATLAB代码绘制不同f下，互信息与$p_1$的关系，以及最优的$p_1$和信道容量。

f = 0.1;
p1s = 0.0001:0.0001:0.9999;
I = [];

for i = 1:length(p1s)
    p1 = p1s(i);
    I(i) = p1*(1-f)*log2(1/(p1*(1-f))) + (1-p1*(1-f))*log2(1/(1-p1*(1-f)))...
        -p1*(f*log2(1/f)+(1-f)*log2(1/(1-f)));
end

[maxv, idx] = max(I)
p1s(idx)

figure(1),clf,plot(p1s,I)

• 对称信道：对称信道的转移概率矩阵，每一行是其他行的置换，每一列是其他列的置换。容量$C(Q)=\log |A_Y|-H(\mathbf{r})$ bits。$H(\mathbf{r})$为矩阵中一行代表的概率分布的熵。最优输入分布为均匀分布。
• 弱对称信道：弱对称信道的转移概率矩阵，每一行是其他行的置换，每一列之和相等。其容量同对称信道，$C(Q)=\log |A_Y|-H(\mathbf{r})$ bits。最优输入分布为均匀分布。

信道容量的属性

• $C\le \log |A_X|$
  因为$I(X;Y)=H(X)-H(X|Y)\le H(X)\le \log |A_X|$。
• $C\le \log |A_Y|$
  因为$I(X;Y)=H(Y)-H(Y|X)\le H(Y)\le \log |A_Y|$。
• $C\ge 0$
  因为$I(X;Y)=H(X)-H(X|Y)\ge 0$（条件降低熵）
• 在已知转移概率矩阵时，$I(X;Y)$是$P(x)$的凸函数。
  这个属性意味着，如果最优分布没有显式解，至少可以用梯度下降找到数值解，而且局部极大值就是全局极大值。这里不做证明，而是给出两个例子供直观理解。对于BSC信道和Z信道，下图显示了互信息与概率分布（唯一的参数$p_1$）的关系。

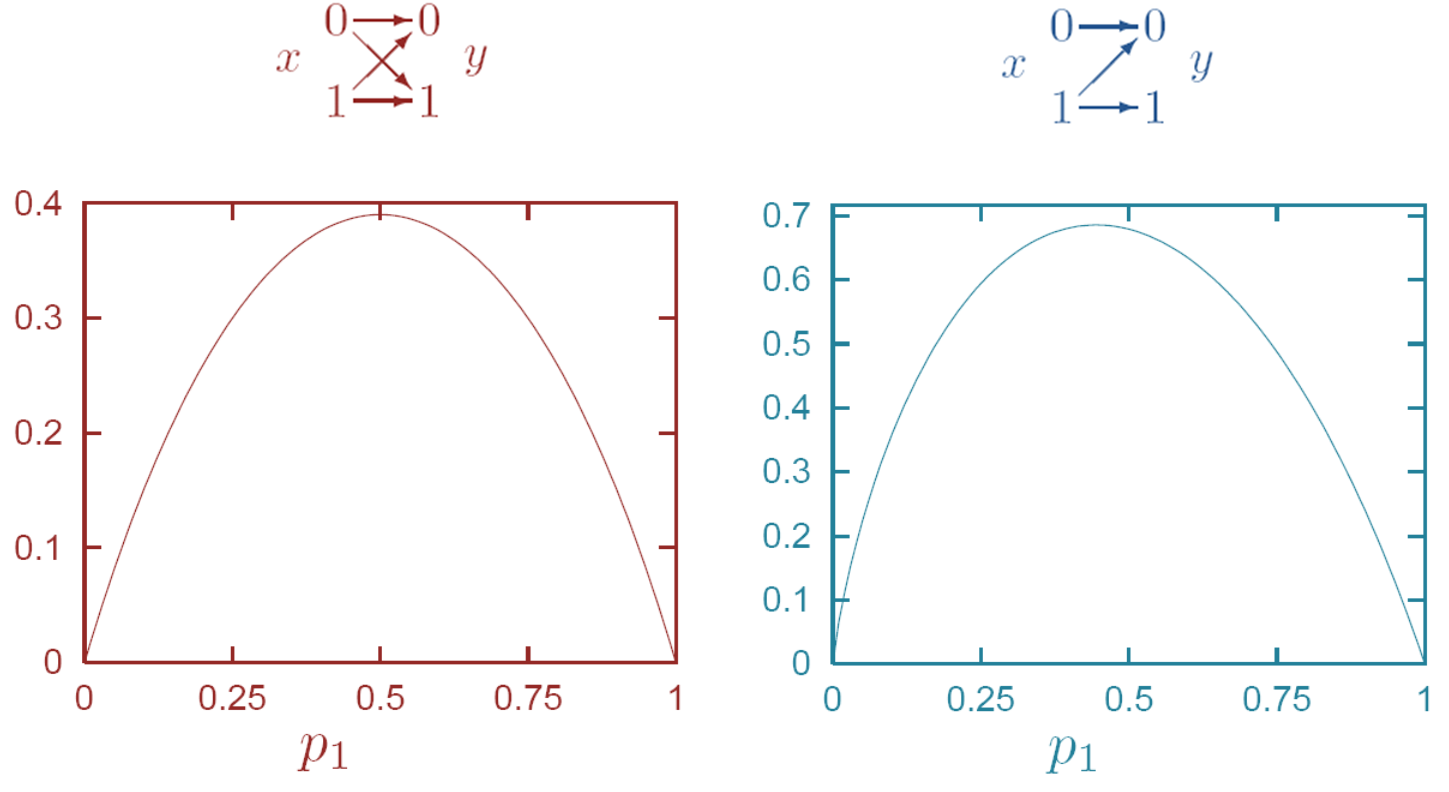
组合信道

并联信道的信道容量为各信道的容量之和。

串联信道的容量有如下特性：
$I(X;Y)\ge I(X;Z)$

一系列$n$个噪声级别为$f$的BSC信道串联。总的转移概率矩阵为：

$Q=\prod _{i=1}^n{Q}_i=\frac{1}{2}\left[\begin{array}{cc}1+(1-2f{)}^n& 1-(1-2f{)}^n\\ 1-(1-2f{)}^n& 1+(1-2f{)}^n\end{array}\right]$

$\underset{n\to \infty }{\lim }Q=\left[\begin{array}{cc}0.5& 0.5\\ 0.5& 0.5\end{array}\right]$
相当于$f=0.5$的BSC信道，其容量为0。说明当串联信道的数目趋于无穷时，总体上已经完全无法传递信息了。

在很久很久以前，我看过一期快乐大本营。其中有个游戏。台上有几名观众排成一排，彼此之间用隔板隔开。主持人告诉第一名观众一个词语，他通过表演动作把信息传递给下一个人。下一个人再继续表演动作，传递给下一个人。直到最后一人。主持人问最后一个人，词语是什么。那一次，词语是泰坦尼克号。第一名观众表演了Jack和Rose在船头的经典动作。随着多人传递，动作越来越变形。当主持人问最后一人这是哪部电影时，她回答是风筝。

对于不得不采用串联信道的场景，例如古时候需要很多烽火台接力传递信息，为了避免级联信道容量趋于0，只能把每个子信道的$f$控制得非常小（假设烽火是BSC信道）。士兵要把烽火点大一些，要认真放哨。