机器学习基石11：线性模型分类（Linear Models for Classification）

本文介绍了用于分类任务的线性模型。主要包括：三种用于线性二分类的模型，随机梯度下降(SGD)，多分类逻辑回归和多分类问题的两种处理方法（OVA，OVO）。

---

---

11. Linear Models for Classification

11.1 Linear Models for Binary Classification

前十节课程讲了三类模型：线性二元分类，线性回归，logistic回归。其共同点为假设函数和误差函数中都使用了 线性得分函数（linear scoring function），公式为：

$s=W^TX$

三类模型与得分s之间的关系如下图所示。

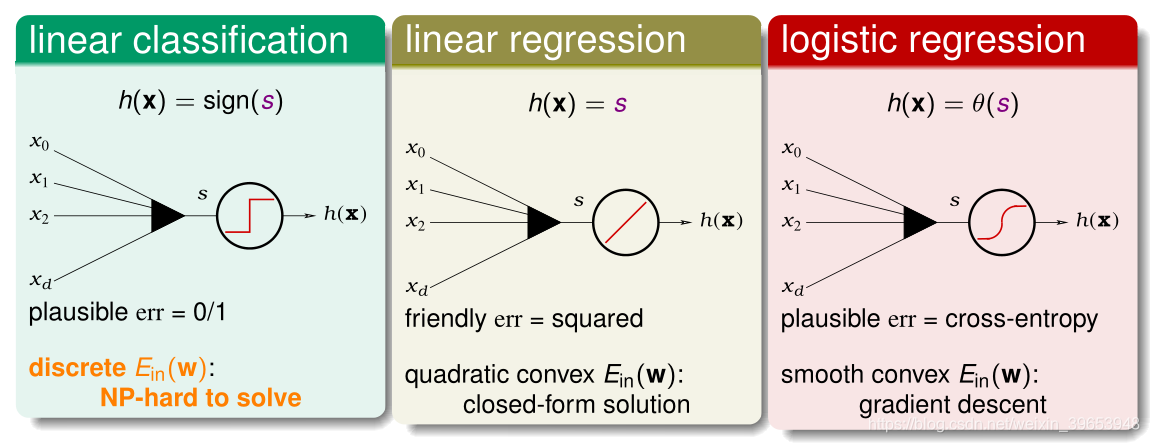
指标\模型	线性分类	线性回归	逻辑回归
假设函数	$h(x) = sign(s)$	$h(x) = s$	$h(x) = \theta(s)$
误差函数	$err = 0/1$	$err = squared$	$err = cross-enropy$
权重向量 $w$ 求解	通过 $E_{in}(w)$ 求解比较困难	可求解析解	梯度下降求解近似值

从上述分析不难看出，线性二元分类问题的求解方式最为困难，但三类模型的假设函数都与得分s有关，能否利用这两种模型的算法近似求得二分类问题的最优 $w$ 呢？首先看一下三个模型的误差函数：

二元分类模型和线性回归模型错误函数中的转换都用到了 $y ∈ \{−1,+1\}$ 性质。上式中， $ys$ 的物理意义是正确的得分 ，因此 $ys$ 越大越好，表示两者接近且同号。

下面用图形化的方式解释三种模型的误差函数之间的关系。

• 0/1 误差（0/1 error）：蓝色线，当ys>0时， $err_{0/1} = 0$ ，反之， $err_{0/1} = 1$ ；

• 平方误差（squared error）：红色线，当ys $\ll$ 0时与 $err_{0/1}$ 在该范围内所表现出的特征相似，但是在ys $\gg$时，远大于 $err_{0/1}$，因此只有在 $err_{SQR}$ 很小的情况下，才能用 $err_{SQR}$ 替代 $err_{0/1}$ 。

• 交叉熵误差（cross-entropy error）：灰色线，同理，只有在 $err_{CE}$ 很小的情况下， 才能用 $err_{CE}$ 替代 $err_{0/1}$ ，但是还需要缩放 $err_{CE}$ 才能替代，于是得到 $err_{SCE}$。因此可以得到：

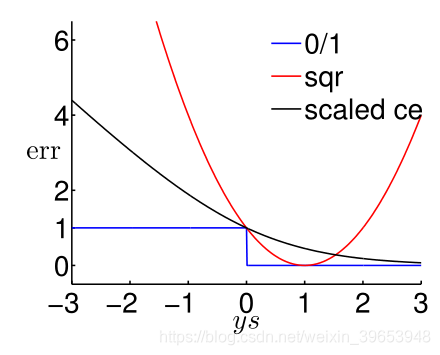
由上图可知， $err_{SCE}$ 可作为 $err_{0/1}$ 的上界，在很小的情况下，可以替代 $err_{0/1}$。

于是得到：

由VC限制理论可得：

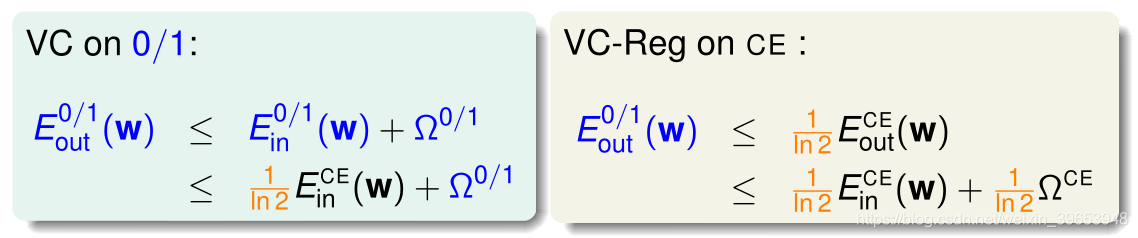
其中， $\Omega^{0/1}$ 、 $\Omega^{CE}$ 均表示模型复杂度。因此得到如下结论：

即较小的 $E^{0/1}_{out}(w)$ 可由较小的 $E^{CE}_{in}(w)$ 推知，同理可证明也可由较小的 $E^{SQR}_{in}(w)$ 得出。

算法的一般流程如下：

• 在输出空间 $y_n∈ \{−1,+1\}$ 的情况下，通过线性回归和逻辑回归相对应的求解方法，求出最优的 $w_{REG}$；
• 将求得的 $w_{REG}$ 代入公式 $sign()$，得到最优的假设函数 $sign(w^T_{REG}x)$。

三类模型比较：

通常使用线性回归模型来获得初始化权重 $w_0$ ，然后使用logistic回归模型进行优化求解。

---

习题1：

---

11.2 Stochastic Gradient Descent

两种迭代优化方法对比：

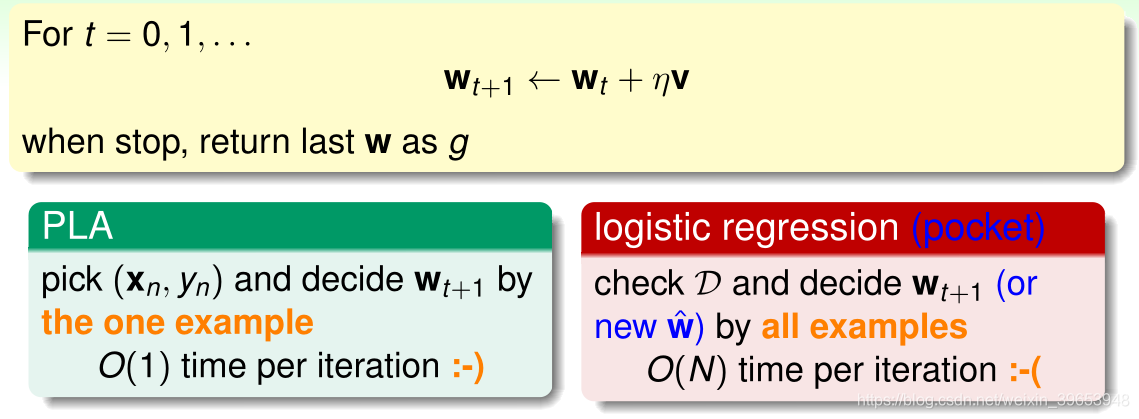
对比PLA与logistic回归的梯度下降算法，发现PLA只需要通过一个样本点便可计算出 $w_{t+1}$，即每次迭代的时间复杂度为 $O(1)$ ；logistic回归的梯度下降需要遍历所有的样本点才能计算出 $w_{t+1}$，即每次迭代的时间复杂度为 $O(N)$ 。有无可能将logistic回归每次迭代时间复杂度降为 $O(1)$ ？

先回顾以下Logistic回归的权重更新公式：

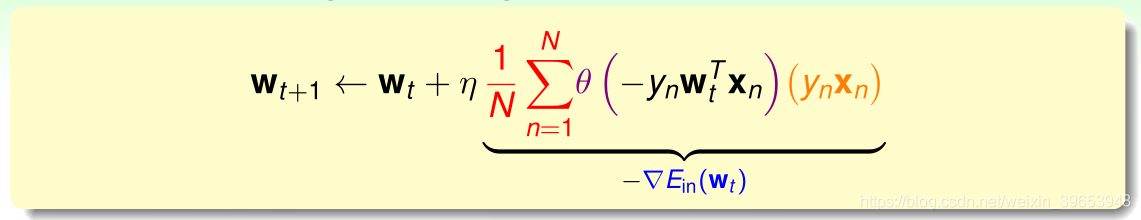
由上式可知，梯度更新的方向向量为 $v \approx -∇E_{in}(w_t)$ ，该梯度是通过所有的样本点加权求和再取平均得到的，那么有没有办法使得用一个样本点的取值来近似整体的平均值呢？

可以将求平均的过程理解为求期望值。在N个样本中随机抽取一个样本点，用这个点求出的梯度取代原来的期望梯度（整体的梯度看成这个随机过程的一个期望值），这种随机选取的梯度称为随机梯度（stochastic gradient），可用符号 $∇_werr(w,x_n,y_n)$ 表示，随机梯度与梯度的关系为：

随机梯度值可以看做真实的梯度值加上一个噪音，使用随机梯度取代真实梯度做梯度下降的算法称作随机梯度下降算法（stochastic gradient descent），简称SGD。这种替代的理论基础是在迭代次数足够多的情况下，平均的随机梯度和平均的真实梯度相差不大。

该算法的优点是简单，容易计算，适用于大数据或者流式数据；缺点是不稳定，每次迭代并不能保证按照正确的方向前进，而且达到最小值需要迭代的次数比梯度下降算法一般要多。

Logistic回归的随机梯度下降的权重迭代公式为：

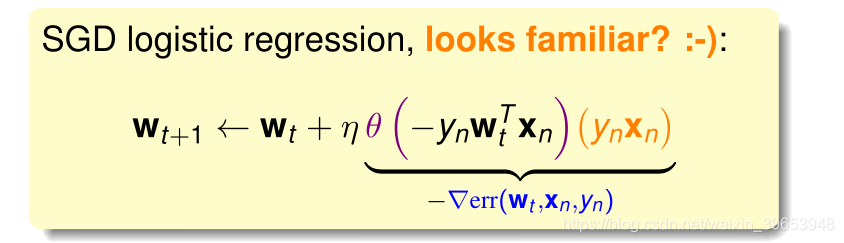
PLA与SGD两种优化算法对比：

logistic回归随机梯度下降类似于"软"的PLA，原因是梯度更新公式中 权重更新的方向 $-y_n w^T_n x_n$ 的取值并非0或1，而是一个在0~1之间的值。当学习速率 $\eta = 1$ 并且 $w^T_t x_n$ 很大的时候，logistic回归随机梯度下降相当于 PLA 。

SGD需要调试两个参数：迭代步骤 $t$ 和学习速率 $\eta$。设置迭代步骤是因为不知道真实的梯度值是否接近0，只能假设足够步数后是已经做到足够好，即通常设置一个大的数值作为步数；学习速率 $\eta$ 通常也很难选定，针对不同的任务和模型，一般有一个公认的参考值，具体还要根据自己的业务需求调整。

---

习题2：

---

11.3 Multiclass via Logistic Regression

多分类任务在识别（recognition）领域有很多应用场景。用一个简单的例子引入本小节要分析的问题：

输出空间y为四类，即 $Y = \{□,◇,△,☆\}$。

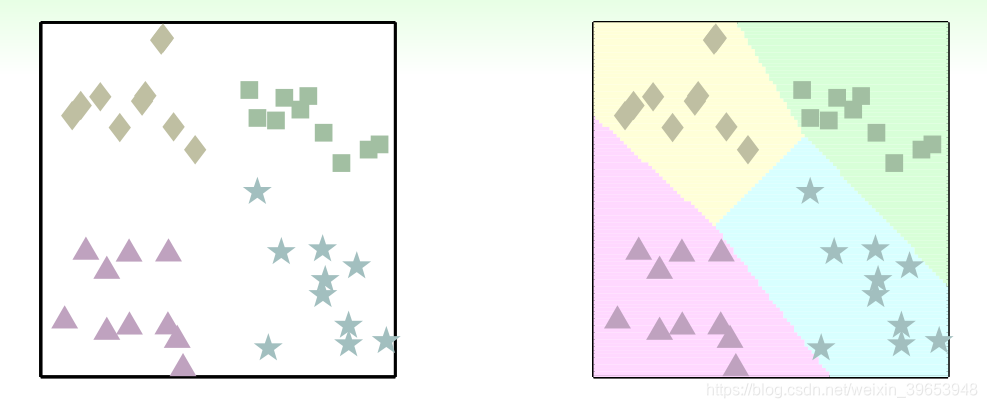
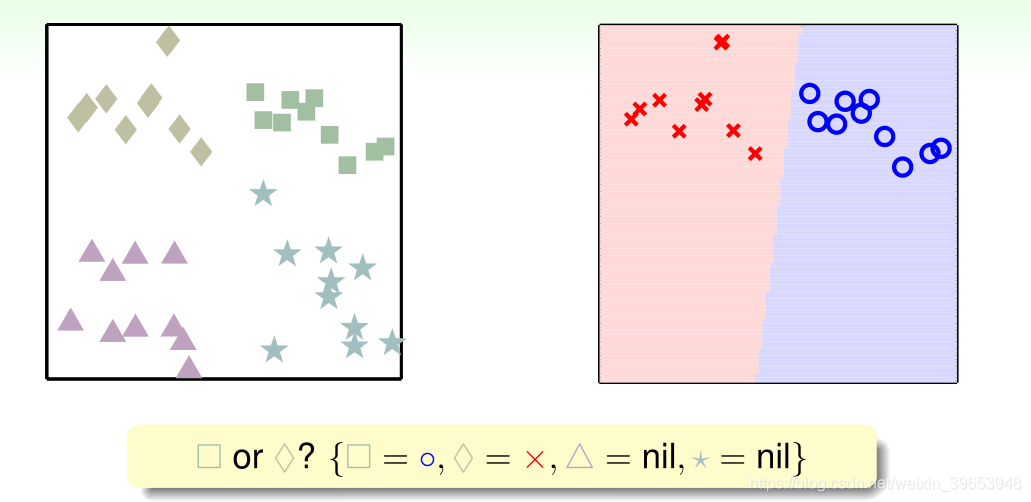
多类别问题也可以用二元分类 $\{×,○ \}$ 的思路进行分类，如将四类分类问题分解为是否为 □，生成一个新的二元分类问题 $Y = \{□ = ○,◇ = ×,△ = ×,☆ = × \}$，通过此方式得到一个分类超平面，如下图所示：

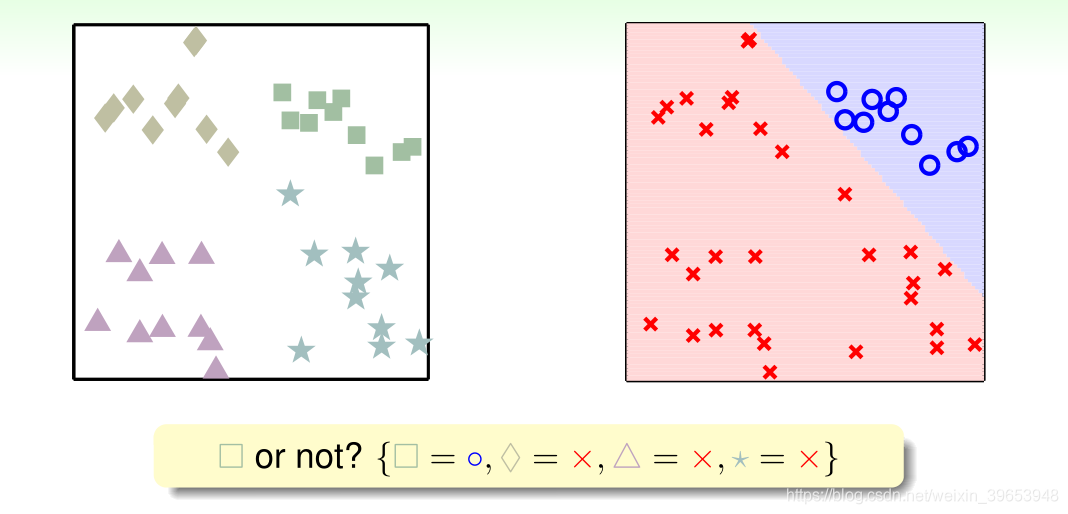
同样的有：

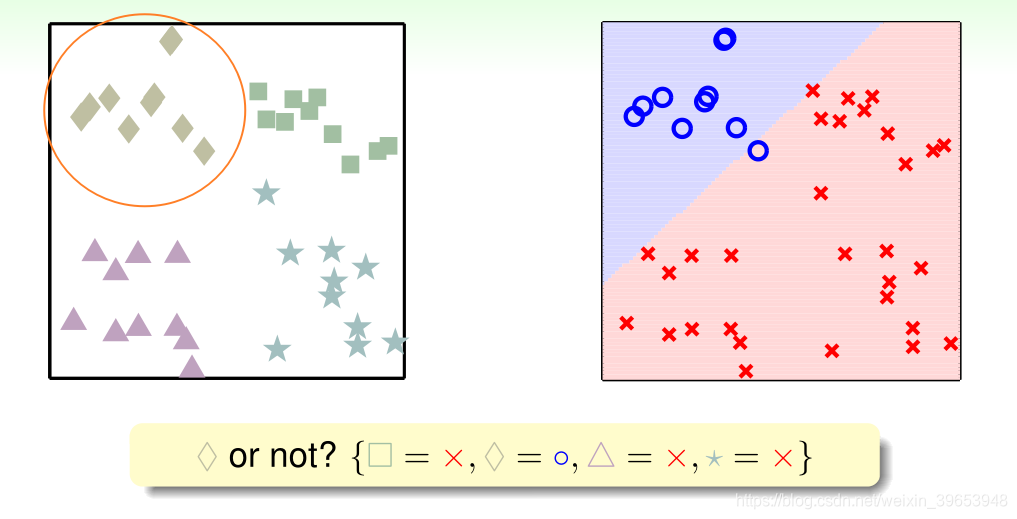
四种分类结果为：

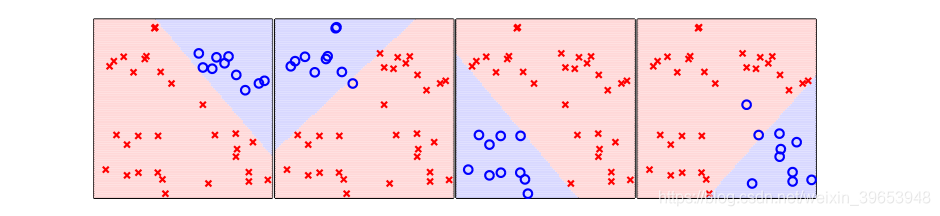
综合四种分类结果可得：

可以看到，有一些无法处理的情形。其中，四个边缘的三角阴影区域为相邻两个类别都争夺的区域，图正中的菱形区域不属于任何类别。这些问题如何解决？

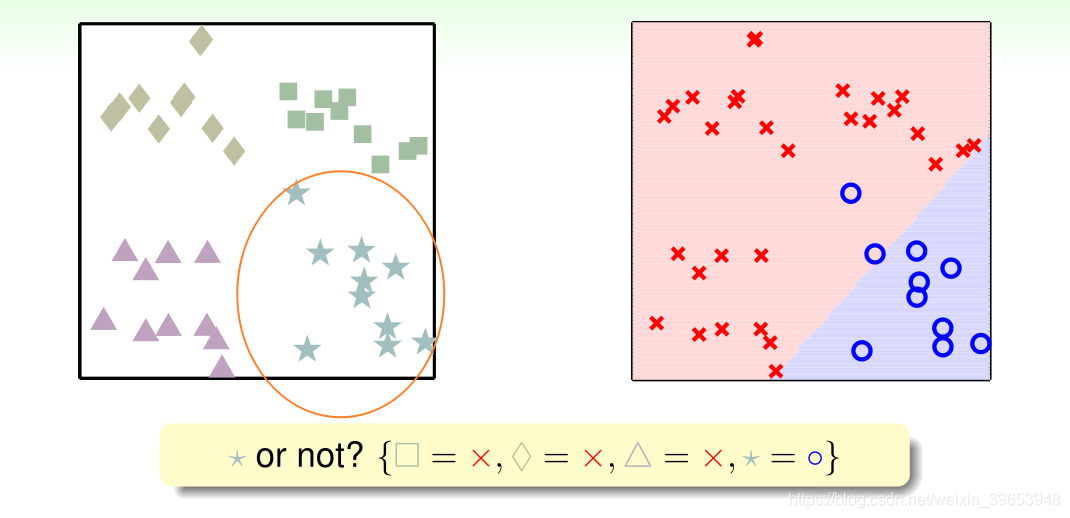
使用“软”分类，还是关于类别 □ 的二元分类问题，此处不再使用硬划分，而是使用该样本点是 □ 的可能性，即 $P(□|x)$ ，如下图所示：

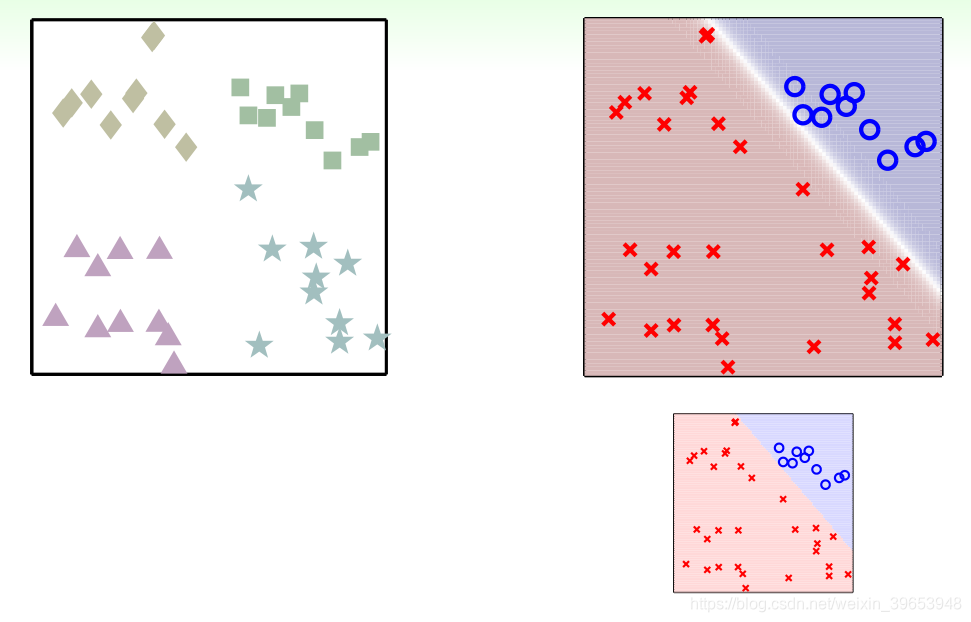
其余情况同理，四种类别的“软”二元分类情况如下图所示：

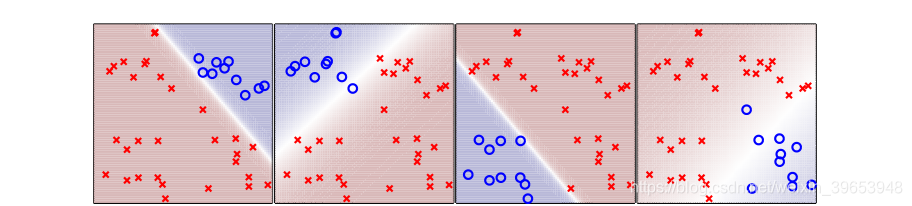
综合四种分类结果有：

那么应该如何判断样本点属于哪个类别？可以分别计算样本点在四种软二元分类情况下概率，选择其中概率最大的一个作为所属类别，计算公式如下：

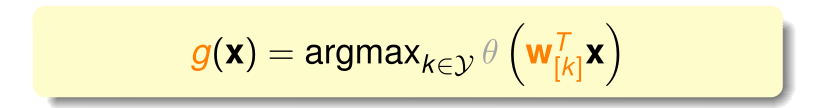
公式使用logistic函数 $\theta$ 求概率 ，k表示类别，由于logistic函数是单调函数，因此可以消去该函数，直接使用类别的得分值 s 作比较。用此种思路设计的算法称作一对多（One Versue All, OVA），算法流程如下：

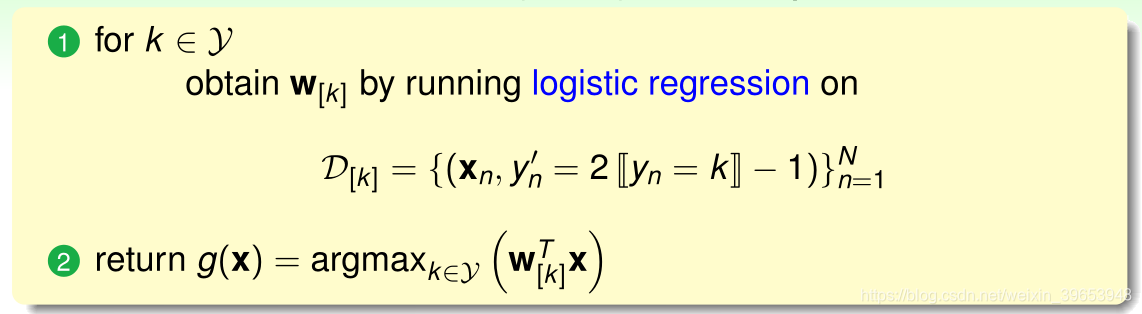
• 在整个训练数据集 $D$ 上， $D_{[k]} = \{(x_n,y_n=2[[y_n=k]]−1)\}^N_{n=1}$，其中， 符号 $[[·]]$表示取1或取0，当 $y=k$ 时为+1， $y≠k$ 时为-1 ；
• 使用logistic函数计算各个类别的权重向量 $w^T_{[k]}$ ；
• 计算假设函数g(x)。

该算法的优点是简单有效，易于类似于logistic函数的二元分类问题扩展成多类别分类；缺点是当类别特别多时，产生了不平衡的现象（如类别特别多，则+1的数据量就很少，大部分都是-1，数据量严重不平衡）。

---

习题3：

---

11.4 Multiclass via Binary Classification

针对OVA（一对多）在类别非常多的情况下训练数据严重失衡的情况，本小节介绍一种应对这类不平衡问题的方法。

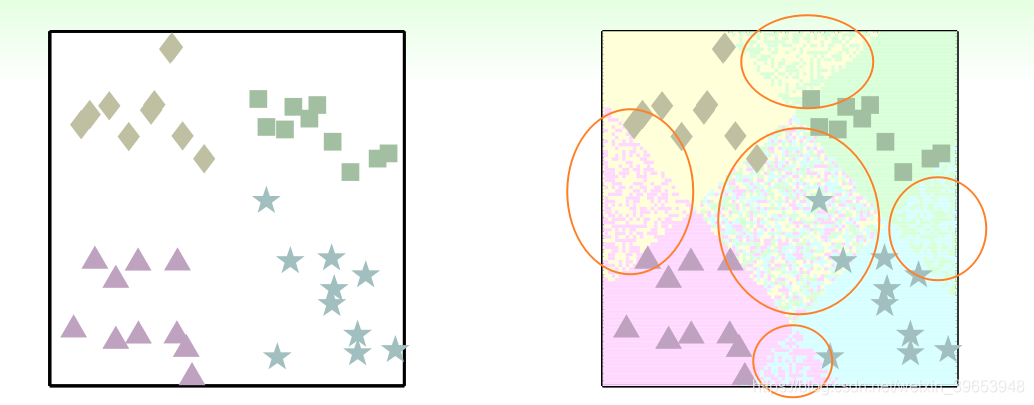
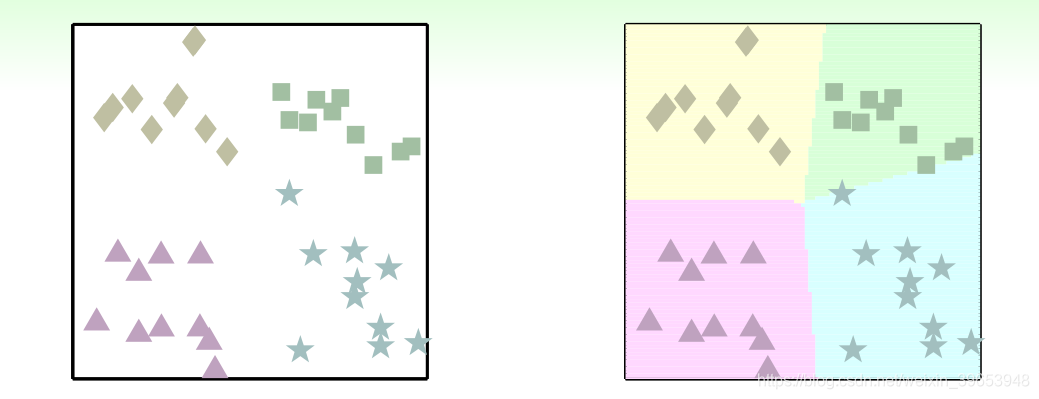
还是上小节中使用的四分类问题，不像OVA在整个数据集中计算是否为□的权值向量w，此种方法是任意选择四类中的两类，将两个类别分别设为+1和-1，在包含两类的数据集上计算权值向量w，如下图所示：

其它情况同理，从四种类别中选取两种做二元分类，一共可得6种（ $C^2_4 = 6$）二分类情况，结果如下：

那么，如何判断某新进样本属于哪个分类？由上例分析，6次二分类之后，如果数据集中的一个样本，有三个分类器判断它是正方形；一个分类器判断是菱形；另外两个分类器判断是三角形；那么取最多的那个，即判断它属于正方形，至此分类完成。

将以上6种二分类组成分类器进行分类，分类结果如下图所示：

这种分类方式称为一对一（One Vervuse One, OVO）。其算法流程如下：

• 从所有类别中任选两个进行二分类，共产生 $C^2_K$ 种分类情况；
• 在数据集 $D$ 上求出最佳的权值向量 $w_{[k,l]}$ ；
• 通过投票返回假设函数 $g$。

这种方法的优点是更加高效，每次使用两类的训练数据，然后根据投票机制汇总不同的二分类结果，虽然分类次数增加，但是单次分类的数量减少，一般不会出现数据不平衡的情况。缺点是需要分类的次数多（ $C^2_K$） ，时间复杂度（ $O(K^2)$）比较高，需要花费更多的存储空间、计算时间。

---

习题4：

---

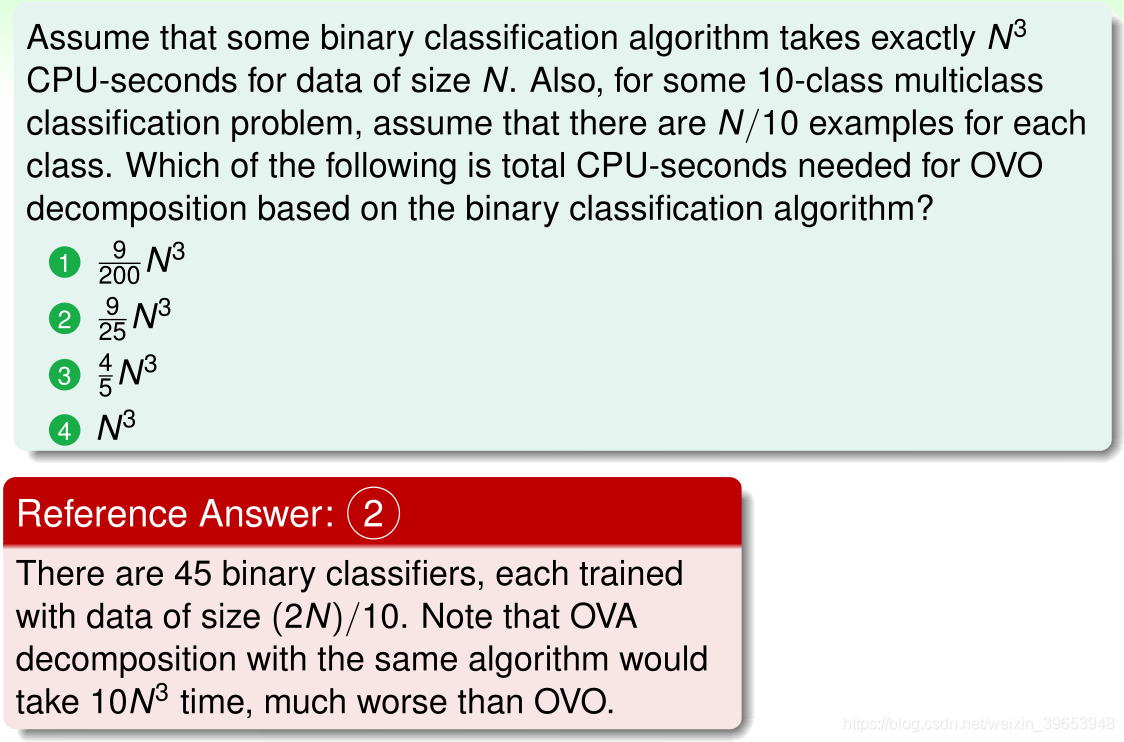
Summary

本节课首先介绍了分类问题的三种线性模型线性分类、线性回归和logistic 回归，这三种模型都能处理二分类任务。

然后介绍了比梯度下降算法更加高效的SGD算法来进行logistic 回归分析。

最后讲解了两种多分类方法，一种是OVA（一对多），另一种是OVO（一对一）。这两种方法各有优缺点，当类别数量K不多的时候，建议选择OVA，以减少分类次数。

---

参考：
https://www.cnblogs.com/ymingjingr/p/4306666.html
https://github.com/RedstoneWill/HsuanTienLin_MachineLearning