【数论】逆元

用途

由于除法不能取模，所以出现了乘法逆元这种东西
(a/b)%p 等同于 求取 a∗(b的逆元)%p

费马小定理

因为在算法竞赛中模数p总是质数，所以可以利用费马小定理 ：

b^(p−1)%p=1

可以直接得到 b^(p-2)即为b在 mod p 意义下的逆元

ll pow(ll a, ll n, ll p)    //快速幂 a^n % p
{
    
    
    ll ans = 1;
    while(n)
    {
    
    
        if(n & 1) ans = ans * a % p;
        a = a * a % p;
        n >>= 1;
    }
    return ans;
}

ll niyuan(ll a, ll p)   //费马小定理求逆元
{
    
    
    return pow(a, p - 2, p);
}

扩展欧几里德

对于利用拓展欧几里德算法求逆元，很显然，如果bx%p=1，那么 bx+py=1（p=0,解x),直接利用 exgcd(b, p, x, y)，则 (x%p+p)%p 即为 b 的逆元((x%p+p)%p为x的最小正整数解)。

void exgcd(ll a, ll b, ll &x, ll &y)    //拓展欧几里得算法
{
    
    
    if(!b) 
        x = 1, y = 0;
    else
    {
    
    
        exgcd(b, a % b, y, x);
        y -= x * (a / b);
    }
}

ll niyuan(ll a, ll b)   //求a对b取模的逆元
{
    
    
    ll x, y;
    exgcd(a, b, x, y);
    return (x + b) % b;
}

例题

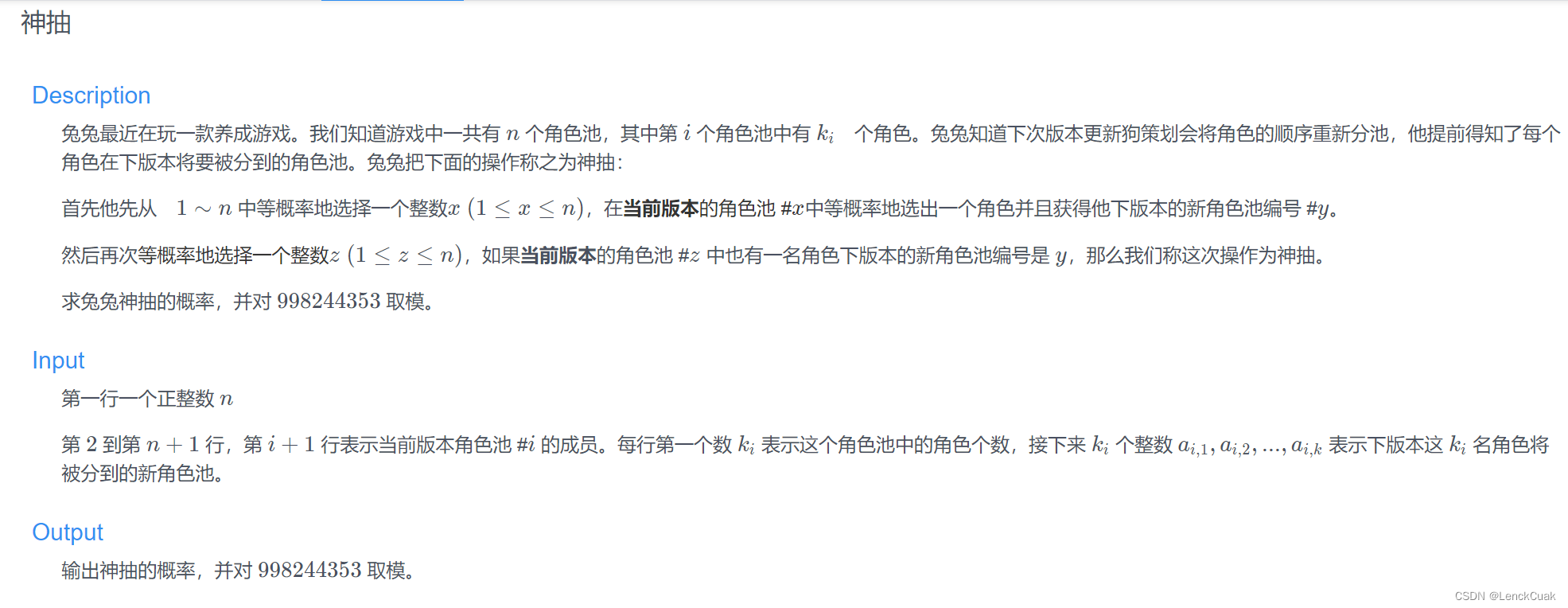
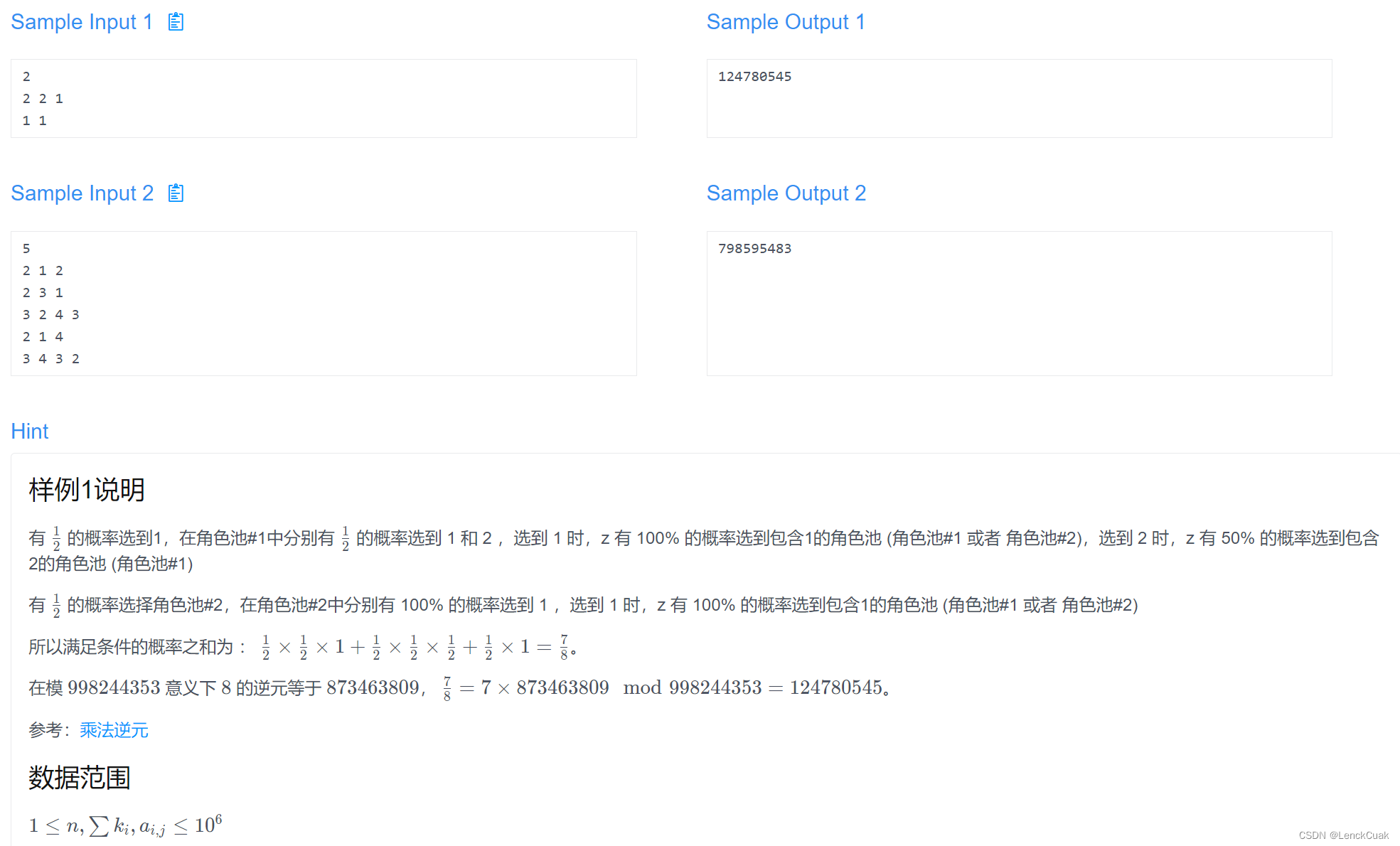
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define P 998244353
ll powmod(ll a,ll n, ll p)
{
    
    
	ll ans=1;
	while(n)
	{
    
    
		if(n&1)ans=ans*a%p;
		a=a*a%p;
		n>>=1;
	}
	return ans;
}
ll c[1000010];
ll f[1000010];
int main() {
    
    
	ios::sync_with_stdio(0);
	int n;
	cin >> n;
	for(int i=0;i<n;i++)
	{
    
    
		int k;
		cin>>k;
		for(int j=0;j<k;j++)
		{
    
    
			int e;
			cin>>e;
			c[e]++;
			f[e]=(f[e]+powmod(n,P-2,P)%P*powmod(k,P-2,P)%P)%P;
		}

	}
	ll ans=0;
	for(int i=1;i<=1e6;i++)
	{
    
    
		ans=(ans+c[i]*f[i]%P*powmod(n,P-2,P)%P)%P;
	}
	cout<<ans<<endl;
	return 0;
}

参考文献

https://www.cnblogs.com/-citywall123/p/10673212.html