回文字符串问题

什么是回文字符串？
「正向和反向观察得到的字符串顺序是相同的」或者「关于中心对称的字符串」
比如字符串：abcba 和 abccba，都是回文串

常用的判断回文子串相关的两种方法：「中心扩展」和「动态规划1」
判断回文子序列的方法一般是「动态规划2」

此外还有一种在线性时间内求解最长回文子串的算法：Manacher 算法

中心扩展法

基于回文字符串对称性的特点，我们可以采取从中心向两边扩展的方法，得到回文子串，回文中心分为两种情况，以单个字母为中心和以两个字母为中心：
1）以单个字母为回文中心

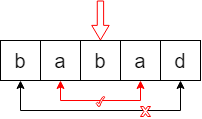
2）以两个字母为回文中心

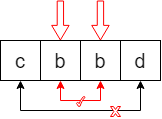
假设字符串长度为 $l e n$ ，则回文中心一共有 $2 \times l e n - 1$ 个，分别是 $l e n$ 个单字符和 $l e n - 1$ 个双字符。
总结：「中心扩展法」的思想就是遍历以一个字符或两个字符为中心可得到的回文子串。中心拓展法适用于连续子串是否是回文串的判断，不太适用于不连续子序列是否是回文串的判断。
连续子序列一般用第二类动态规划方法，状态量 $d p [i] [j]$ 为字符串在 $[i, j]$ 区间的回文序列个数（int 类型）。

第一类动态规划法

由于长字符串会依赖短字符串的回文串，所以我们可以采用动态规划来实现。

这里需要二维的 $d p [] []$ 数组，设置状态量： $d p [i] [j]$ 表示字符串 $s$ 在 $[i, j]$ 区间的子串是否是一个回文串。
当我们判断 $[i .. j]$ 是否为回文子串时，只需要判断 $s [i] == s [j]$ ，同时判断 $[i - 1.. j - 1]$ 是否为回文子串即可
需要注意有两种特殊情况： $[i, i]$ or $[i, i + 1]$ ，即：子串长度为 1 或者 2。所以需要加一个条件限定 $j - i < 2$
状态转移方程如下：

dp[i][j] = (s[i] == s[j]) && (j - i < 2 || dp[i + 1][j - 1])

解释：当 $\&\& (j - i < 2 || dp[i + 1][j - 1])$ 时， $d p [i] [j] = t r u e$ ，否则为 $f a l se$

Manacher （马拉车）算法

复杂度为 O(n) 的Manacher 算法是在线性时间内求解最长回文子串的算法。也可以用于求解回文串的个数。

Manacher 的基本原理：
定义一个新概念臂长，表示中心扩展算法向外扩展的长度。如果一个位置的最大回文字符串长度为 2 * length + 1 ，其臂长为 length。

Manacher 算法也会面临奇数长度和偶数长度的问题，它的处理方式是在所有的相邻字符中间插入 $\#$ ，比如 $abaa$ 会被处理成 $\#a\#b\#a\#a\#$ ，这样可以保证所有找到的回文串都是奇数长度的，以任意一个字符为回文中心，既可以包含原来的奇数长度的情况，也可以包含原来偶数长度的情况。假设原字符串为 S，经过这个处理之后的字符串为 s。

我们用 f(i) 来表示以 s 的第 i 位为回文中心，可以拓展出的最大回文半径，那么 f(i) - 1 就是以 i 为中心的最大回文串长度。
（后续内容详见超链接，此方法只做了解）

回文子串问题

回文子串问题一般用中心拓展与第一类动态规划方法求解。
可以用这道题的题解当模板，进行理解学习：
647. 回文子串
给你一个字符串 s ，请你统计并返回这个字符串中回文子串的数目。
回文字符串 是正着读和倒过来读一样的字符串。
子字符串 是字符串中的由连续字符组成的一个序列。
具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。

示例 1：
输入：s = “abc”
输出：3
解释：三个回文子串: “a”, “b”, “c”

示例 2：
输入：s = “aaa”
输出：6
解释：6个回文子串: “a”, “a”, “a”, “aa”, “aa”, “aaa”

法一：中心拓展法
「中心扩展法」的思想就是遍历以一个字符或两个字符为中心可得到的回文子串，分两种情况调用isPalindromic(string s, int i, int j)函数。

//法一：中心扩展法
 	int ans = 0;
    int countSubstrings(string s) {
    
    
        int n = s.size();
        for(int i = 0; i < n; ++i){
    
    
        	// 以单个字母为中心的情况
            isPalindromic(s, i, i);
            // 以两个字母为中心的情况
            isPalindromic(s, i, i + 1);
        }
        return ans;
    }
    void isPalindromic(string s, int i, int j){
    
    
        while(i >= 0 && j < s.size()){
    
    
            if(s[i] != s[j]) return;
                ++ans;
                ++j;
                --i;
        }
    }

中心拓展法的另一种解法：
长度为 $n$ 的字符串会生成 $2 n - 1$ 组回文中心 $l_i, r_i]$ ，其中 $l_i = i/2$ ， $r_i = l_i + (i \% 2)$ 。这样我们只要从 $0$ 到 $2 n - 2$ 遍历 $i$ ，就可以得到所有可能的回文中心，这样就把奇数长度和偶数长度两种情况统一起来了。

	int countSubstrings(string s) {
    
    
        int n = s.size();
        int num = 0;
        for(int i = 0; i < 2 * n - 1; ++i){
    
    
            int l = i / 2;
            int r = l + ( i % 2);
            while(l >= 0 && r < n && s[l] == s[r]){
    
    
                ++num;
                --l;
                ++r;
            }
        }       
        return num;
    }

法二：动态规划
由于长字符串会依赖短字符串的回文串数量，所以我们可以采用动态规划来实现。
$d p [i] [j]$ 表示字符串 $s$ 在 $[i, j]$ 区间的子串是否是一个回文串，当 $s [i] == s [j]$ 时，如果 $d p [i] [j]$ 是回文串，则要么 $[i, j]$ 区间仅有一个或两个字符，要么 $d p [i + 1] [j - 1]$ 是一个回文串

	//法二：动态规划  
	//dp[i][j] 表示字符串s在[i,j]区间的子串是否是一个回文
	//当 s[i]==s[j] 时，要么[i, j]区间仅有一个或两个字符，要么看 dp[i+1][j-1] 是不是一个回文串    
    int countSubstrings(string s) {
    
    
        int n = s.size();
        int ans = 0;
        //n行n列，其实只用到下三角
        vector<vector<bool>> dp(n, vector<bool>(n));
        for(int j = 0; j < n; ++j){
    
    
            for(int i = 0; i <= j; ++i){
    
    
                if(s[i] == s[j] && (j - i < 2 || dp[i + 1][j - 1])){
    
    
                    dp[i][j] = true;
                    ++ans;
                }
            }
        }
        return ans;
    }

用下面这道题加深对上面模板的套用和理解。
5. 最长回文子串
给你一个字符串 s，找到 s 中最长的回文子串。

示例 1：
输入：s = “babad”
输出：“bab”
解释：“aba” 同样是符合题意的答案。

法一：中心扩展法
还是沿用了上一题的模板，唯一的改动就是记录一下最长子串的起始点和长度。

	//法一：中心扩展法
	int maxi = 0, maxlen = 0;
    string longestPalindrome(string s) {
    
    
        int n = s.size();
        for(int i = 0; i < n; ++i){
    
    
            ispalindromic(s, i, i);
            ispalindromic(s, i, i + 1);
        }
        return s.substr(maxi, maxlen);
    }
    void ispalindromic(string& s, int i, int j){
    
    
        while(i >= 0 && j < s.size()){
    
    
            if(s[i] != s[j]) return;
            if(j - i + 1 > maxlen){
    
    
                maxi = i;
                maxlen = j - i + 1;
            }
            --i;
            ++j;
        }
    }

法二：动态规划
由于长字符串会依赖短字符串的回文串长度，所以我们可以采用动态规划来实现。
沿用了上一题的模板，唯一的改动就是记录一下最长子串的起始点和长度。
$d p [i] [j]$ 表示字符串 $s$ 在 $[i, j]$ 区间的子串是否是一个回文串，当 $s [i] == s [j]$ 时，如果 $d p [i] [j]$ 是回文串，则要么 $[i, j]$ 区间仅有一个或两个字符，要么 $d p [i + 1] [j - 1]$ 是一个回文串

	//法二：动态规划
	string longestPalindrome(string s) {
    
    
        int maxi = 0,  maxlen = 0;
        int n = s.size();
        vector<vector<bool>> dp(n, vector<bool>(n));
        for(int j = 0; j < n; ++j){
    
    
            for(int i = 0; i <= j; ++i){
    
    
                if(s[i] == s[j] && (j - i < 2 || dp[i + 1][j - 1])){
    
    
                    dp[i][j] = true;
                    if(j - i + 1 > maxlen){
    
    
                        maxlen = j - i + 1;
                        maxi = i;
                    }
                }
            }
        }
        return s.substr(maxi, maxlen);
    }

回文子序列问题

回文子序列问题一般用第二类动态规划解法。
这几道题需要另外一种动态规划状态量定义方法。状态量 $d p [i] [j]$ 改为字符串在 $[i, j]$ 区间的回文序列个数（int 类型）了，而不是之前的字符串 $s$ 在 $[i, j]$ 区间的子串是否是一个回文串（布尔类型）了。然后按照序列长度 $l e n$ 进行动态规划。可以理解为另外一套动态规划模板。
516. 最长回文子序列
对于一个子序列而言，如果它是回文子序列，并且长度大于 2，那么将它首尾的两个字符去除之后，它仍然是个回文子序列。因此可以用动态规划的方法计算给定字符串的最长回文子序列。

①状态量的定义
用 $\textit{dp}[i][j]$ 表示字符串 s 的下标范围 $[i, j]$ 内的最长回文子序列的长度。假设字符串 s 的长度为 n，则只有当 $\le i \le j < n$ 时，才会有 $\textit{dp}[i][j] > 0$ ，否则 $\textit{dp}[i][j] = 0$ （在二维数组中已经默认置为0了，不需要额外操作）。

②边界初始化
由于任何长度为 1 的子序列都是回文子序列，因此动态规划的边界情况是，对任意 $\le i < n$ ，都有 $\textit{dp}[i][i] = 1$ 。

③状态转移方程推导
当 $i < j$ 时，计算 $\textit{dp}[i][j]$ 需要分别考虑 $s [i]$ 和 $s [j]$ 相等和不相等的情况：

1）如果 $s [i] = s [j]$ ，则首先得到 s 的下标范围 $[i + 1, j - 1]$ 内的最长回文子序列，然后在该子序列的首尾分别添加 $s [i]$ 和 $s [j]$ ，即可得到 s 的下标范围 $[i, j]$ 内的最长回文子序列，因此 $\textit{dp}[i][j] = \textit{dp}[i+1][j-1] + 2$ ；

2）如果 $\ne s[j]$ ，则 $s [i]$ 和 $s [j]$ 不可能同时作为同一个回文子序列的首尾，因此 $\textit{dp}[i][j] = \max(\textit{dp}[i+1][j], \textit{dp}[i][j-1])$ ，注意这里要取两头各自去掉一个字符情况中的最大值，而不是只有一种同时去掉两头的情况。

由于状态转移方程都是从长度 $l e n$ 较短的子序列向长度较长的子序列转移，因此需要注意动态规划的循环顺序。

最终得到的 $\textit{dp}[0][n-1]$ 即为字符串 $s$ 的最长回文子序列的长度。

	int longestPalindromeSubseq(string s) {
    
    
        int n = s.size();
        if(n == 0){
    
    
            return 0;
        }
        vector<vector<int>> dp(n, vector<int>(n));
        //只有当 0≤i≤j<n 时，才会有 dp[i][j]>0，否则 dp[i][j]=0（在二维数组中已经默认置为0了，不需要额外操作）
        // for(int i = 0; i < n - 1; ++i){
    
    
        //     dp[i + 1][i] = 0; 
        // }
        for(int i = 0; i < n; ++i){
    
    
            dp[i][i] = 1;
        }
        for(int len = 2; len <= n; ++len){
    
    
            for(int i = 0; i + len <= n; ++i){
    
    
                int j = i + len - 1;
                if(s[i] == s[j]){
    
    
                    dp[i][j] = dp[i + 1][j - 1] + 2;
                }else{
    
    
                //注意这里要取两头各自去掉一个字符情况中的最大值，
                //而不是只有一种同时去掉两头的情况
                    dp[i][j] = max(dp[i][j - 1], dp[i + 1][j]);
                }
            }
        }
        return dp[0][n - 1];
    }

下面这道题也是相似的解法，不过难度更大一些。

730. 统计不同回文子序列
给定一个字符串 s，返回 s 中不同的非空「回文子序列」个数。
通过从 s 中删除 0 个或多个字符来获得子序列。子序列不一定连续，仅保证前后顺序一致。
如果一个字符序列与它反转后的字符序列一致，那么它是「回文字符序列」。
如果有某个 $i$ , 满足 $a_i != b_i$ ，则两个序列 $a_1, a_2, ...$ 和 $b_1, b-2, ...$ 不同。

注意：
结果可能很大，你需要对 $10^9 + 7$ 取模。

示例 1：
输入：s = ‘bccb’
输出：6
解释：6 个不同的非空回文子字符序列分别为：‘b’, ‘c’, ‘bb’, ‘cc’, ‘bcb’, ‘bccb’。
注意：‘bcb’ 虽然出现两次但仅计数一次。

示例 2：
输入：s =‘abcdabcdabcdabcdabcdabcdabcdabcddcbadcbadcbadcbadcbadcbadcbadcba’
输出：104860361
解释：共有 3104860382 个不同的非空回文子序列，104860361 对 109 + 7 取模后的值。

【解答】
由于长字符串会依赖短字符串的回文序列数量，所以我们可以采用动态规划来实现。
设 $d p [i] [j]$ 表示字符串从 $i$ 到 $j$ 的回文序列个数，我们可以将长字符串看作短字符串左右加上两个字符。
于是我们有 $s [i, j] = s [i] + s [i + 1, j - 1] + s [j]$ ，如：“bccb” 可以看作 “cc"两边分别加上"b”，此时我们分情况进行讨论
(1)若 $s [i] == s [j]$ ，相当于我们给 $s [i + 1, j - 1]$ 左右加上两个相同的字符，然后我们计算回文序列的个数。

① $s [i + 1, j - 1]$ 中没有字符和 $s [i]$ 相等
设有字符串"bcb"，则"bcb"的回文子序列是：b、c、bb、bcb
若两边加上相同的字符，相当于给"bcb"的回文子序列左右个加一个相同字符，仍然构成回文子序列
假设我们给"bcb"左右加一个字符"a"，则相当于给"bcb"的子序列都左右加一个字符可构成新的回文子序列：

再加上"a"(字符本身就是一个回文子序列)和"aa"(两个相同字符的回文子序列)
所以此时 $d p [i] [j] = 2 d p [i + 1] [j - 1] + 2$ （本身的4个+新生成的4个+2个单独生成的）

② $s [i + 1, j - 1]$ 中有一个字符和s[i]相等
假设有一个字符相等，则之前已经记录了此单字符的回文子序列(只能加上"aa"，不能加"a")
所以此时 $d p [i] [j] = 2 d p [i + 1] [j - 1] + 1$ （本身的4个+新生成的4个+1个单独生成的）

③ $s [i + 1, j - 1]$ 中有两个及以上字符和 $s [i]$ 相等
若有两个及以上的字符,则我们需要找到其位置，并删掉重复计算的回文子序列，并且两个单独的之前也已经计算。
假设有字符串"dabcbad"，我们向两边加入字符"a"
则此时的"a"字符会和中间的"bcb"组成重复的回文子序列，因为之前已经有"a"和"bcb"组成回文子序列

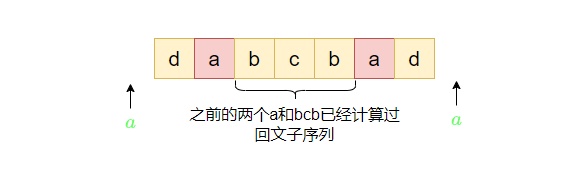
(2)若 $s [i]! = s [j]$ ，则我们给之前任何一个回文子序列左右加上 $s [i]$ 和 $s [j]$ 都不能组成回文子序列，只能单独计算

综上所述，状态转移方程为：

按照序列长度 $l e n$ 进行动态规划，可保证长序列计算时短序列的结果都已经出来，可以直接使用子问题保存的结果。
【注意点】
int 是32位的，第一位是符号位，最大正值是 $2^{31}$ ，取值范围是-2147483648（10位）——2147483647，如果超出最大值就会产生进位将符号位置1，变成负数。因此当数量很大时，常常需要对大质数 $10^9 + 7$ 取模%运算，使结果变小，当然答案也会做相应处理。在C++中， $10^9 + 7$ 用1e9+7表示。仅有加法运算时，最后直接取模缩小就行，当还有减法时，还需要对负数加模运算。

	int countPalindromicSubsequences(string s) {
    
    
        int MOD = 1e9+7; //当结果很大时，需要对大质数10^9 + 7取模%运算，使结果变小，答案也会进行相应处理
        int n = s.size();
        vector<vector<int>> dp(n, vector<int>(n));
        //因为要求子序列无重复，因此按照序列长度进行动态规划，
        //而不是按照j不断向右扩张的[i,j]序列进行动态规划，这样可能导致重复
        //长度为1的[i,j]序列，一个单字符是一个回文子序列
        for(int i = 0; i < n; ++i){
    
    
            dp[i][i] = 1;
        }
        //按照序列长度len进行动态规划，可保证长序列计算时短序列的结果都已经出来，可以直接用
        //从长度为2的子串开始计算
        for(int len = 2; len <= n; ++len){
    
    
        //挨个计算长度为len的子串的回文子序列个数
            for(int i = 0; i + len <= n; ++i){
    
    
                int j = i + len - 1;
                //情况(1) 相等
                if(s[i] == s[j]){
    
    
                    int l = i + 1, r = j - 1;
                    //找到第一个和s[i]相同的字符
                    while(l <= r && s[l] != s[i]) ++l;
                    //找到第一个和s[j]相同的字符
                    while(r >= l && s[r] != s[j]) --r;
                     //情况① 没有重复字符
                    if(l > r) dp[i][j] = 2 * dp[i + 1][j - 1] + 2;
                    //情况② 出现一个重复字符
                    else if(l == r) dp[i][j] = 2 * dp[i + 1][j - 1] + 1;
                    //情况③ 有两个及两个以上
                    else dp[i][j] = 2 * dp[i + 1][j - 1] - dp[l + 1][r - 1];
                }else{
    
    
                //情况(2) 不相等
                    //前面的每个dp值都已经取过模，很大的int也会缩小了，因此减法运算时可能会出现负数
                    //仅有加法运算时，最后直接取模缩小就行，当还有减法时，还需要对负数加模运算
                    dp[i][j] = dp[i + 1][j] + dp[i][j - 1] - dp[i + 1][j - 1];
                }
                //处理超范围结果,signed integer overflow
                //如果超出int最大值就会产生进位将符号位置1，变成负数。
                dp[i][j] = dp[i][j] >= 0 ? dp[i][j] % MOD : dp[i][j] + MOD;
            }
        }
        return dp[0][n - 1];
    }