因子图学习笔记其三

Reference:

1. Frank Dellaert 《机器人感知-因子图在SLAM中的应用》

还没写完，占个坑。

3. 探索稀疏性

正如我们在之前的章节所看到的那样，在非线性 SLAM 的例子中进行最大后验概率推断，需要迭代求解大型 (但是稀疏) 的线性系统。尽管有一些高效的软件库可用来求解大型稀疏线性系统，但是求解线性系统本身也仅仅是一个更加通用的算法的特例。稀疏线性系统只是线性高斯因子图的一种特殊形式，即所有的先验和观测都被假设是符合高斯分布的，并且只涉及线性观测函数。因子图的稀疏结构是理解这个更加通用的算法的关键因素，也是理解(和改进)稀疏分解方法的关键因素。

3.1 关于稀疏性

3.1.1 启发性的例子

求解稠密线性系统的方法无法应用于大规模真实 SLAM 问题。在第 1 章中我们用了一个小问题来解释贝叶斯网络和因子图，在这个例子中，稠密的方法也可以运行得很好。第二章图中所展示的那个规模大一点的 SLAM 例子中的因子图，可以更好地表达真实世界中的问题。然而，与真正的 SLAM 问题相比，这个例子的规模还是显得太小了，真实世界中几千甚至数百万未知量的问题也都是可以见到的。然而，有了稀疏性，我们就完全可以处理这些问题。

通过直接观察因子图，我们就可以意识到稀疏性的存在。可以很容易看出第二章图中的因子图是稀疏(sparse)的，即它不可能是一个全连接图。连接着 100 个未知位姿的里程计链，是一个有着 100 个二元因子的线性结构，而不可能是 $100^2$ 个（二元）因子。另外，在有 20 个路标点的情况下，图中最多可以存在 2000(20*100) 个连接路标点和位姿的似然因子：实际上真实的情况大约是 400 个(路标和里程计间互相看不到是常态)。路标点之间没有因子，说明我们没有任何关于它们之间相对位置的信息，这是大部分 SLAM 问题中的典型结构。

下面，我们将深入理解这些问题的稀疏结构。我们使用第 1 章中的小型 SLAM 问题作为贯穿本章的例子。然后，在本章的结尾路标我们将展示如何将这些概念用在更大型的系统，以及真实世界的问题中。

3.1.2 稀疏雅可比矩阵及其因子图

大多数现代 SLAM 算法的一个关键特点是利用了稀疏性。SLAM 中因子图的一个重要性质是：它们可以表示导出雅可比矩阵 $\mathbf{A}$ 中的稀疏块结构。为了观察稀疏块结构，让我们重新回顾非线性 SLAM 问题迭代步骤中的关键计算步骤------最小二乘。
$${\Delta }^{\ast }=\underset{\Delta }{\mathrm{argmin}}\sum _i{\Vert {\mathbf{A}}_i{\mathbf{\Delta }}_i-b_i\Vert }_2^2$$

上式中的每一项都由原始非线性 SLAM 问题中的一个因子推导而来，并在当前线性点处进行线性化(线性化看2.3节)$\begin{array}{r}{\Delta }^{\ast }=\underset{\Delta }{\mathrm{argmin}}\sum _i{\Vert {\mathbf{H}}_i{\mathbf{\Delta }}_i-\left\{z_i-h_i\left({\mathbf{X}}_i^0\right)\right\}\Vert }_{{\mathbf{\Sigma }}_i}^2\end{array}$。矩阵 $A_i$ 可以按照变量分成对应的块，被收集到一个大型的块稀疏雅可比矩阵中，并且其稀疏结构直接由因子图决定。

这些线性问题产生于非线性优化的内部迭代过程，下面我们会忽略 $\mathbf{\Delta }$ 符号，并考虑如何解决通用的线性问题。

例子

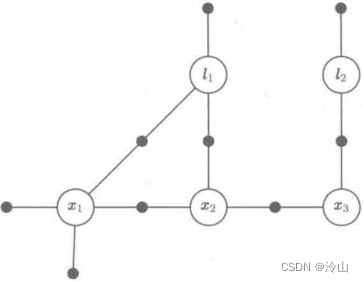
考虑之前的小型 SLAM 例子，方便起见，我们再将它放到下左图中。在线性化之后，我们得到了一个有着下面右图所示块结构的稀疏系统 $[A\mid b]$ 。将右图与因子图进行对比，很明显，每一个因子对应 $A$ 的一个块行，而每一个变量对应 $A$ 的一个块列。总共有 9 个块行，对应 $\varphi \left(l_1,l_2,x_1,x_2,x_3\right)$ 分解过程中的每一个因子(这里跟普通SLAM开始有区别了，在ORB中倾向于对$u,v$求雅克比，所以一般只有两行，而这里是每个因子一个块行)。

3.1.3 稀疏信息矩阵及其图表示

我们在 $2.4$ 节中解释过，当使用乔里斯基分解求解正规方程时，首先计算海森矩阵或者信息矩阵(Hessian矩阵在最大似然（MLE）问题中被认为约等于信息矩阵，所以一般也会将Hessian矩阵直接当做信息矩阵对待) $\mathbf{\Lambda }={\mathbf{A}}^{\top }\mathbf{A}$ 。通常，由于雅可比矩阵 $\mathbf{A}$ 是块稀疏的，因而海森矩阵 $\mathbf{\Lambda }$ 也将是稀疏的。通过海森矩阵的构造方法可知其对称，并且如果存在唯一的最大后验概率解，那么海森矩阵还将是正定的。

信息矩阵 $\mathbf{\Lambda }$ 也可以与另一个被称作马尔可夫随机场(markov random field, MRF) 的无向图模型相对应，它们也是用来对 SLAM 问题进行表示的。与因子图相比，马尔可夫随机场是一个只涉及变量的图模型，就像一个贝叶斯网络一样。但是与贝叶斯网络不同的是，马尔可夫随机场中的图 $G$ 是一个无向图：其中的边只表示它所连接的变量之间有部分关联。从块上来看，$\Lambda =A^{\top }A$ 的稀疏模式就是图 $G$ 的邻接矩阵。

例子

下面的海森矩阵图 $\mathbf{\Lambda }\stackrel{\text{ def }}{=}{A}^{\top }\mathbf{A}$ 展示了与我们运行的小型 SLAM 例子对应的信息矩阵 $\mathbf{\Lambda }$ 。如图所示，这个例子中有 5 个变量(${\Lambda }_{11},{\Lambda }_{22},{\Lambda }_{33},{\Lambda }_{44},{\Lambda }_{55}$)将海森矩阵划分开。那些值为 $0$ 的块表示变量之间没有关联，例如，$l_1$ 和 $l_2$ 之间就没有直接的联系(${\Lambda }_{12}$和${\Lambda }_{21}$均为$0$)。
$$\left[\begin{array}{lllll}{\Lambda }_{11}& & {\Lambda }_{13}& {\Lambda }_{14}& \\ & {\Lambda }_{22}& & & {\Lambda }_{25}\\ {\Lambda }_{31}& & {\Lambda }_{33}& {\Lambda }_{34}& \\ {\Lambda }_{41}& & {\Lambda }_{43}& {\Lambda }_{44}& {\Lambda }_{45}\\ & {\Lambda }_{52}& & {\Lambda }_{54}& {\Lambda }_{55}\end{array}\right]$$

下图展示了相应的马尔可夫随机场：

接下来，我们要大量涉及与推断问题相关的马尔可夫随机场所对应的无向图 $G$。然而，除此之外，我们不会过多地使用马尔可夫随机场的图模型。注意，我们可以开发出一个对等的理论，用来解释马尔可夫随机场如何表示不同类型的因子概率密度，关于这个理论可以参考 Koller 和 Friedman 的文献。例如，在线性-高斯的情况下，最小二乘误差可以被重写如下：
$$\begin{array}{rl}\Vert \mathbf{A}\mathbf{\Delta }-\mathbf{b}{\Vert }_2^2& ={\mathbf{\Delta }}^{\top }{\mathbf{A}}^{\top }\mathbf{A}\mathbf{\Delta }-2{\mathbf{\Delta }}^{\top }{\mathbf{A}}^{\top }\mathbf{b}+{\mathbf{b}}^{\top }\mathbf{b}\\ & ={\mathbf{b}}^{\top }\mathbf{b}-2\sum _j{\mathbf{g}}_j^{\top }{\mathbf{\Delta }}_j+\sum _{ij}{\mathbf{\Delta }}_i^{\top }{\mathbf{\Lambda }}_{ij}{\mathbf{\Delta }}_j\end{array}$$

式中，$\mathbf{g}\stackrel{\text{ def }}{=}{\mathbf{A}}^{\top }\mathbf{b}$。对上式求指数幂后，得到的高斯密度函数有如下形式:
$$p(\mathbf{\Delta })\propto \exp \left(-\Vert \mathbf{A}\mathbf{\Delta }-\mathbf{b}{\Vert }_2^2\right)\propto \prod _j{\varphi }_j\left({\mathbf{\Delta }}_j\right)\prod _{ij}{\psi }_j\left({\mathbf{\Delta }}_i,{\mathbf{\Delta }}_j\right)$$

这也是二元马尔可夫随机场推导出的概率密度的通用形式。

然而，因子图更适合我们的需求。它们可以表示一个更细粒度的分解，并且与原始问题更为接近。例如，如果在因子图中存在三元 (或者更多元) 的因子，那么与马尔可夫随机场等价的图 $G$ 连接了无向团 (一个全连接子图 ) 中的节点，但是团势能就在转换成马尔可夫随机场的过程中丢失了。在线性代数中，这反映了一个事实：有很多矩阵 $A$ 都可以生成相同的信息矩阵 $\mathbf{\Lambda }=A^{\top }A$，这会导致关于稀疏性的重要信息丢失。

3.2 消元算法

给定任意一个 (最好是稀疏的) 因子图，存在一个通用算法，可以计算出未知变量 $\mathbf{X}$ 的后验概率密度 $p(\mathbf{X}\mid Z)$，因此可以很容易地得到求解问题的最大后验概率解。正如我们所看到的那样，因子图将未归一化的后验概率 $\varphi (X)\propto$ $P(\mathbf{X}\mid Z)$ 表示为一系列因子的乘积。在 SLAM 问题中，因子图通常直接由观测量生成(还是说的${\mathbf{z}}_{k,j}=h\left({\mathbf{y}}_j,{\mathbf{x}}_k\right)+{\mathbf{v}}_{k,j}$，即概率观测模型)。消元算法是一种将因子图转换回贝叶斯网络的方法，但是它现在仅仅转换未知量 $\mathbf{X}$。这使得最大后验概率推断、采样 (之前提到过)，以及边缘化(marginalization)变得很容易。

特别地，变量消元(variable elimination)算法是一种将因子图 $\varphi (X)=\varphi \left(x_1,\cdots ,x_n\right)$

分解为如下表示形式的因子化贝叶斯网络概率密度。
$$p(\mathbf{X})=p\left({\mathbf{x}}_1\mid {\mathbf{S}}_1\right)p\left({\mathbf{x}}_2\mid {\mathbf{S}}_2\right)\cdots p\left({\mathbf{x}}_n\right)=\prod _{j}p\left({\mathbf{x}}_j\mid {\mathbf{S}}_j\right)$$

我们选定变量消元顺序为 ${\mathbf{x}}_1,\cdots ,{\mathbf{x}}_n$，与变量 ${\mathbf{x}}_j$ 相关的分离器(separator) $\mathcal{S}\left({\mathbf{x}}_j\right)$ 记为 $S_j$。分离器是这样一组变量的集合：在 ${\mathbf{x}}_j$ 被消去后，${\mathbf{x}}_j$ 在这组变量上被条件化。这个分解过程与链式法则相似，并且对一个稀疏因子图进行消元会产生小的分离器。

算法 $3.1$ 展示了消元算法的流程(大的消元流程)，我们用简写的符号 ${\Phi }_{j:n}\stackrel{\text{ def }}{=}\varphi \left(x_j,\cdots ,x_n\right)$ 表示一个部分消元的因子图。算法以完整的因子图 ${\Phi }_{1:n}$ 开始，每次对一个变量 ${\mathbf{x}}_j$ 进行消元(从$l$的第一个开始消元，一直消元到$x$的最后一个)。每当消去一个变量 ${\mathbf{x}}_j$，函数 EliminateOne 就会生成一个单独的条件概率 $p\left(x_j\mid S_j\right)$，以及在剩余变量上的一个简化后的因子图 ${\Phi }_{j+1:n}$(留下其他的因子图项(还没来得及消元)，并得到这次消元的条件概率$p\left(x_j\mid S_j\right)$)。当所有的变量都被消去后，算法返回期望分解的贝叶斯网络。
(图中意思就是一直消元到最后一个)

算法 $3.2$ 给出了对单个变量 ${\mathbf{x}}_j$ 消元的伪代码(每一个变量具体是怎样消元的)。给定一个部分消元的因子图 ${\Phi }_{j:n}$，我们首先移除与 $x_j$ 相邻的所有因子 ${\varphi }_i\left(x_i\right)$，将其乘以乘积因子 $\psi \left(x_j,S_j\right)$。然后，将 $\psi \left({\mathbf{x}}_j,{\mathbf{S}}_j\right)$ 分解为一个在消元变量 ${\mathbf{x}}_j$ 上的条件概率分布 $p\left({\mathbf{x}}_j\mid {\mathbf{S}}_j\right)$，以及在分离器 $\mathcal{S}\left({\mathbf{x}}_j\right)$ 上的一个新的因子 $\tau \left(S_j\right)$(可见下图中产生的红色因子)：
$$\psi \left({\mathbf{x}}_j,{\mathbf{S}}_j\right)=p\left({\mathbf{x}}_j\mid {\mathbf{S}}_j\right)\tau \left({\mathbf{S}}_j\right)$$

因此，从 $\varphi (\mathbf{X})$ 到 $p(\mathbf{X})$ 的整个分解过程，可以看作 $n$ 个连续的局部分解步骤。当消元进行到最后一个变量 ${\mathbf{x}}_n$ 时，分离器 $\mathcal{S}\left({\mathbf{x}}_n\right)$ 将变为空集，并且产生的条件概率密度会蜕变为在变量 ${\mathbf{x}}_n$ 上的先验概率密度 $p\left(x_n\right)$。

例子

下图展示了对于小型 SLAM 例子以 ${\mathbf{l}}_1,{\mathbf{l}}_2,{\mathbf{x}}_1,{\mathbf{x}}_2,{\mathbf{x}}_3$ 为消元顺序的一个可能的消元序列。在每一步中，被消元的变量都会变灰，在分离器 $S_j$ 上新产生的因子 $\tau \left({\mathbf{S}}_j\right)$ 显示为红色。总体来说，变量消元算法将因子图 $\varphi \left(l_1,l_2,{\mathbf{x}}_1,{\mathbf{x}}_2,{\mathbf{x}}_3\right)$ 分解为下图所示贝叶斯网络，相应的分解过程如下：
$$\begin{array}{rl}p\left({\mathbf{l}}_1,{\mathbf{l}}_2,{\mathbf{x}}_1,{\mathbf{x}}_2,{\mathbf{x}}_3\right)=& p\left({\mathbf{l}}_1\mid {\mathbf{x}}_1,{\mathbf{x}}_2\right)p\left({\mathbf{l}}_2\mid {\mathbf{x}}_3\right)\\ & p\left({\mathbf{x}}_1\mid {\mathbf{x}}_2\right)p\left({\mathbf{x}}_2\mid {\mathbf{x}}_3\right)p\left({\mathbf{x}}_3\right).\end{array}$$

小型SLAM例子的变量消元过程，从因子图转换到一个贝叶斯网络，消元顺序为 ${\mathbf{l}}_1,{\mathbf{l}}_2,{\mathbf{x}}_1,{\mathbf{x}}_2,{\mathbf{x}}_3$

3.3 利用变量消元进行稀疏矩阵分解

在线性观测函数和高斯加性噪声的例子中，消元算法的过程等价于矩阵分解的过程。稀疏乔里斯基分解和 QR 分解都是通用算法的特例。

3.3.1 稀疏高斯因子

让我们考虑 3.2 节中算法 $3.2$ 所描述的对单个变量 ${\mathbf{x}}_j$ 进行的消元。在最小二乘问题${\Delta }^{\ast }=\underset{\Delta }{\mathrm{argmin}}{\sum }_i{\Vert {\mathbf{A}}_i{\mathbf{\Delta }}_i-b_i\Vert }_2^2$(回顾$\Delta$代表$\Delta x$，$A$代表雅克比)中，所有的因子都具有如下形式：
$${\varphi }_i\left({\mathbf{X}}_i\right)=\exp \left\{-\frac{1}{2}{\Vert {\mathbf{A}}_i{\mathbf{X}}_i-b_i\Vert }_2^2\right\}$$

式中，$X_i$ 是因子 ${\varphi }_i$ 中所涉及的所有变量，而 ${\mathbf{A}}_i$ 则由每个变量所对应的小的子块所组成。

例子

在小型 SLAM 例子中，${\mathbf{l}}_1$ 与 ${\mathbf{x}}_1$ 之间的线性化因子 ${\varphi }_7$ 等于
$${\varphi }_7\left(l_1,{\mathbf{x}}_1\right)=\exp \left\{-\frac{1}{2}{\Vert A_{71}{l}_1+A_{73}{x}_1-b_7\Vert }_2^2\right\}$$

相应地，
$$\begin{array}{l}{A}_7\stackrel{\text{ def }}{=}\left[A_{71}\mid A_{73}\right]\\ {\mathbf{X}}_7\stackrel{\text{ def }}{=}\left[l_1;{\mathbf{x}}_1\right]\end{array}$$

我们用分号来表示列向量的横向合并。

3.3.2 生成乘积因子

如上所述，消元算法每次对一个变量进行处理。根据算法 3.2，对于每个变量 ${\mathbf{x}}_j$，我们移除所有与其相邻的因子 ${\varphi }_i\left({\mathbf{X}}_i\right)$，并生成中间乘积因子 $\psi \left({\mathbf{x}}_j,S_j\right)$ 。将所有矩阵 ${\mathbf{A}}_i$ 合并到一个新的、更大的块矩阵 ${\overline{\mathbf{A}}}_j$ 中，可写为如下形式：
$$\begin{array}{rl}\psi \left({\mathbf{x}}_j,{\mathbf{S}}_j\right)& \leftarrow \prod _i{\varphi }_i\left({\mathbf{X}}_i\right)\\ & =\exp \left\{-\frac{1}{2}\sum _i{\Vert A_i{\mathbf{X}}_i-b_i\Vert }_2^2\right\}\\ & =\exp \left\{-\frac{1}{2}{\Vert {\bar{A}}_j\left[{\mathbf{x}}_j;{\mathbf{S}}_j\right]-{\bar{b}}_j\Vert }_2^2\right\}\end{array}$$

式中，新生成的右侧向量 ${\mathbf{b}}_j$ 合并了所有的 $b_i$。

例子

考虑对小型 SLAM 例子中的变量 $l_1$ 进行消元。与它邻接的因子有 ${\varphi }_4$、${\varphi }_7$ 和 ${\varphi }_8$，因此引入分离器 $S_1=\left[x_1;x_2\right]$。乘积因子等于：
$$\psi \left({\mathbf{l}}_1,{\mathbf{x}}_1,{\mathbf{x}}_2\right)=\exp \left\{-\frac{1}{2}{\Vert {\overline{\mathbf{A}}}_1\left[{\mathbf{l}}_1;{\mathbf{x}}_1;{\mathbf{x}}_2\right]-{\overline{\mathbf{b}}}_1\Vert }_2^2\right\}$$

式中，
$${\overline{\mathbf{A}}}_1\stackrel{\mathrm{def}}{=}\left[\begin{array}{ccc}{A}_{41}& & \\ A_{71}& A_{73}& \\ A_{81}& & A_{84}\end{array}\right],{\overline{\mathbf{b}}}_1\stackrel{\mathrm{def}}{=}\left[\begin{array}{c}{b}_4\\ b_7\\ b_8\end{array}\right]$$

观察图 3-2 中的稀疏雅可比矩阵，上式可以总结如下：将第 1 列非零块所在的行都提取出来，分别对应于和 $l_1$ 邻接的 3 个因子。

3.3.3 利用部分 $\mathrm{QR}$ 分解进行变量消元

可以通过一些不同的方式对乘积因子 $\psi \left(x_j,S_j\right)$ 进行分解。我们首先讨论 $\mathrm{QR}$ 方法，因为它与线性化因子更加相关。特别地，通过部分 $\mathrm{QR}$ 分解可以将与乘积因子 $\psi \left({\mathbf{x}}_j,{\mathbf{S}}_j\right)$ 相对应的增广矩阵 $\left[{\overline{\mathbf{A}}}_j\mid {\overline{\mathbf{b}}}_j\right]$ 转化为：
$$\left[{\overline{\mathbf{A}}}_j\mid {\overline{\mathbf{b}}}_j\right]=\mathbf{Q}\left[\begin{array}{ccc}{\mathbf{R}}_j& {\mathbf{T}}_j& {\mathbf{d}}_j\\ & {\tilde{\mathbf{A}}}_{\tau }& {\tilde{\mathbf{b}}}_{\tau }\end{array}\right]$$

式中，${\mathbf{R}}_j$ 是一个上三角形矩阵。这允许我们按照如下方式对 $\psi \left(x_j,S_j\right)$ 进行分解：
$$\begin{array}{rl}\psi \left({\mathbf{x}}_j,S_j\right)& =\exp \left\{-\frac{1}{2}{\Vert {\overline{\mathbf{A}}}_j\left[{\mathbf{x}}_j;S_j\right]-{\overline{\mathbf{b}}}_j\Vert }_2^2\right\}\\ & =\exp \left\{-\frac{1}{2}{\Vert {\mathbf{R}}_j{\mathbf{x}}_j+{\mathbf{T}}_j{S}_j-{\mathbf{d}}_j\Vert }_2^2\right\}\exp \left\{-\frac{1}{2}{\Vert {\tilde{A}}_{\tau }{S}_j-{\tilde{\mathbf{b}}}_{\tau }\Vert }_2^2\right\}\\ & =p\left({\mathbf{x}}_j\mid S_j\right)\tau \left({\mathbf{S}}_j\right)\end{array}$$

这里我们利用了如下性质: 与旋转矩阵 $Q$ 相乘并不会改变一个向量的 2-范数值。

例子

在下图中，我们展示了对例子中第一个变量 $l_1$ 进行消元的结果，路标点 ${\mathbf{l}}_1$ 对应的分离器为 { x 1 , x 2 } \left\{\boldsymbol{x}_1, \boldsymbol{x}_2\right\} { x1​,x2​}。在图 3-2 中，我们在忽略右侧向量的情况下，展示了在因子图上的操作，还有对稀疏雅可比矩阵的影响。雅可比矩阵在线上面的部分对应着一个正在生成的稀疏上三角形矩阵 $\mathbf{R}$。对矩阵新添加的量用粗体字来表示：蓝色代表矩阵 $\mathbf{R}$ 新添加的量，红色代表新生成的因子。

3.3.4 多波前 $\mathrm{QR}$ 分解

整个消元算法，使用部分 $\mathrm{QR}$ 分解对单个变量进行消元，等价于进行稀疏QR分解(sparse QR factorization)。上面的处理考虑了多维变量 ${\mathbf{x}}_j\in {\mathbb{R}}^{n_j}$，这实际上是一个多波前 $\mathrm{QR}$ 分解的实例，我们每次对多个标量同时进行消元，可以有效地增加处理器的利用率。在我们的例子中，标量分组由推断问题中的语义信息 (变量) 所决定。另外，稀疏线性代数程序库也可以通过分析问题的结构决定标量分组，以提高计算效率。在许多情况下，这两个策略会给出相似的结果。

例子

为了结果的完整性，我们展示了下图中所示消元过程的剩余 4 步，以一个端到端的例子展示了如何在一个小的例子中进行多波前 $QR$ 分解。最后一步展示了生成的贝叶斯网络和稀疏上三角因子 $\mathbf{R}$ 之间的等价性。

3.4 稀疏乔里斯基分解与贝叶斯网络

变量消元和稀疏矩阵分解之间的等价性说明，与一个上三角形矩阵相对应 的图模型正是一个贝叶斯网络！正如一个因子图稀疏雅可比矩阵的图形体现，一个马尔可夫随机场可以与海森矩阵相对应一样，一个贝叶斯网络揭示了一个乔里斯基因子的稀疏性结构。这样再看下面的结论可能就不再感觉惊奇了：一个贝叶斯网络是一个有向无环图(directed acyclic graph, DAG)，这正体现了矩阵的“上三角”性质。

更重要的是，乔里斯基因子对应着一个由一些线性高斯条件组成的高斯贝叶斯网络 (Gaussian Bayes net)。变量消元算法可以处理一般的概率密度函数，但是在因子图只包含线性观测方程和高斯加性噪声的情况下，生成的贝叶斯网络有一个非常特殊的形式。我们将在下面讨论这些细节，同时也会讨论如何在线性情况下求解最大后验概率估计值。

3.4.1 线性高斯条件概率密度

我们在 $3.2$ 节中讨论了一般性的消元算法，通过对贝叶斯网络分解后得到的概率密度 $P(\mathbf{X})$ 进行消元，线性化问题所对应的高斯因子图就会被转换为
$$P(\mathbf{X})=\prod _{j}p\left({\mathbf{x}}_j\mid {\mathbf{S}}_j\right)$$

在 $\mathrm{QR}$ 分解和乔里斯基分解中，条件概率密度 $p\left({\mathbf{x}}_j\mid S_j\right)$ 可以由下式计算:
$$p\left({\mathbf{x}}_j\mid S_j\right)=k\exp \left\{-\frac{1}{2}{\Vert {\mathbf{R}}_j{\mathbf{x}}_j+{\mathbf{T}}_j{\mathbf{S}}_j-{\mathbf{d}}_j\Vert }_2^2\right\}$$

它是消元变量 ${\mathbf{x}}_j$ 的线性高斯密度函数。实际上，我们有：
$${\Vert R_j{x}_j+T_j{S}_j-d_j\Vert }_2^2={\left(x_j-{\mu }_j\right)}^{\top }{R}_j^{\top }{R}_j\left(x_j-{\mu }_j\right)\stackrel{\text{ def }}{=}{\Vert x_j-{\mu }_j\Vert }_{{\Sigma }_j}^2$$

式中，均值 ${\mu }_j=R_j^{-1}\left(d_j-T_j{S}_j\right)$ 线性依赖于分离器 $S_j$，协方差矩阵由 ${\Sigma }_j=$ ${\left({\mathbf{R}}_j^{\top }{\mathbf{R}}_j\right)}^{-1}$ 给出。因此，归一化常数为 $k={\left|2\pi {\mathbf{\Sigma }}_j\right|}^{-1/2}$ 。

3.4.2 反向替代求解贝叶斯网络

在消元步骤完成后，反向替代可以用来获得每个变量的最大后验概率估计值。如图 3-7 所示，最后一个被消去的变量不依赖于其他任何变量。因此，可以直接从贝叶斯网络中获得最后一个变量的最大后验概率估计值。通过将消元的顺序进行逆序，总是可以从之前的步骤得到每一次条件化所对应的所有分离器变量的值，这样就可以计算出当前的前端变量(frontal variable)的估计值。

算法 $3.3$ 总结了求解的过程。在每一步中，变量 ${\mathbf{x}}_j$ 的最大后验概率估计值都是条件均值:
$$x_j^{\ast }=R_j^{-1}\left(d_j-T_j{S}_j^{\ast }\right)$$

至此，我们已经完全了解了如何构建分离器 $S_j^{\ast }$ 的最大后验概率估计值。

3.5 讨论

以上讨论了如何利用消元算法高效地求解由 SLAM 的最大后验概率推断部分生成的线性系统，这些方法对于其他的应用也是通用的。我们着重展示了当对一个单独变量进行消元时，部分 $\mathrm{QR}$ 分解推导出的一个有名的稀疏矩阵分解方法。接下来，一个自然而然的问题是，既然已经存在高效的求解稀疏线性系统的代码和软件库，为什么还要做上面的研究? 作者认为以上工作比较重要的原因是，它从一种新的角度提出了更深的理解，同时也因为消元方法要比线性代数方法更加通用。

研究稀疏线性代数的学者并不喜欢用概率图模型的语言进行解释说明。他们关注线性系统本身，而忽略线性系统的出处。这些线性系统来自不同的领域，如流体力学、飞行器设计或者天气预报等。因此，线性代数软件包需要以一种通用的方式处理不同的问题。然而，在机器人领域，以及其他连续变量估计问题中，用贝叶斯概率及最大后验概率推断进行推断是很有优势的。上面的解释使得它们之间的联系更加明显，并且强调了稀疏线性代数是如何作为计算引擎使用的。

从现实意义上讲，稀疏线性代数分解方法只是一种更加通用算法的特例，并为未来的算法创新提供了可能的思路。我们推导以上算法时，并不要求概率 密度函数必须符合高斯分布，或者必须为连续的变量。可以利用几乎相同的算法，在离散问题上进行最大后验概率推断或边缘化，甚至对混合了离散与连续变量的问题也同样适用。

在接下来的几章中，我们将深人讨论其中的联系，并且以这个新的观点来描述算法。