一.树的概念

提到树我们就不得不提到:线性结构和非线性结构,
线性结构:数据与数据的关系是唯一的!(一对一)
例:顺序表,链表,栈,对列,数组等都是线性结构。
非线性结构:数据与数据的关系不是唯一的!(一对多或者多对一)
例:树形结构。
看如上的图我们可以大概画一张图(倒着画):
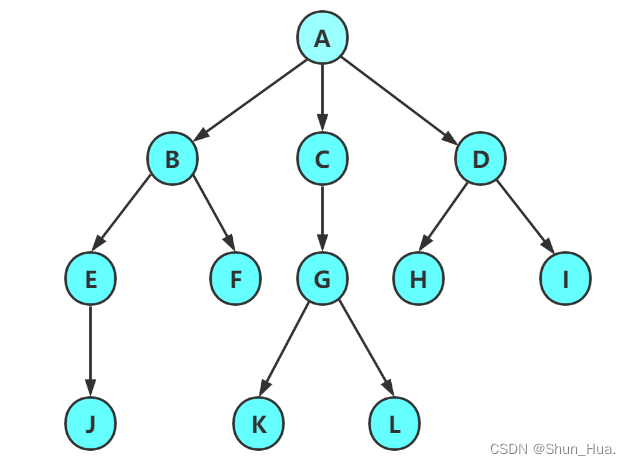
可以得出: 有分支的结点至少一个结点,结点不是唯一的对应关系,有一对多的关系。因此数是非线性结构的。
提问:树的节点可以是0吗?
百度回答:树的节点是大于等于0的!
因此我们可以得出:树的节点是可以为0的!n=0,为空树
但是:节点为0的可不一定是树哦!
因此我们可以得出树的两个概念:
1.节点大于等于0
2.满足非线性结构
子树:
树能分为:
1.根节点
2.子树/叶子节点
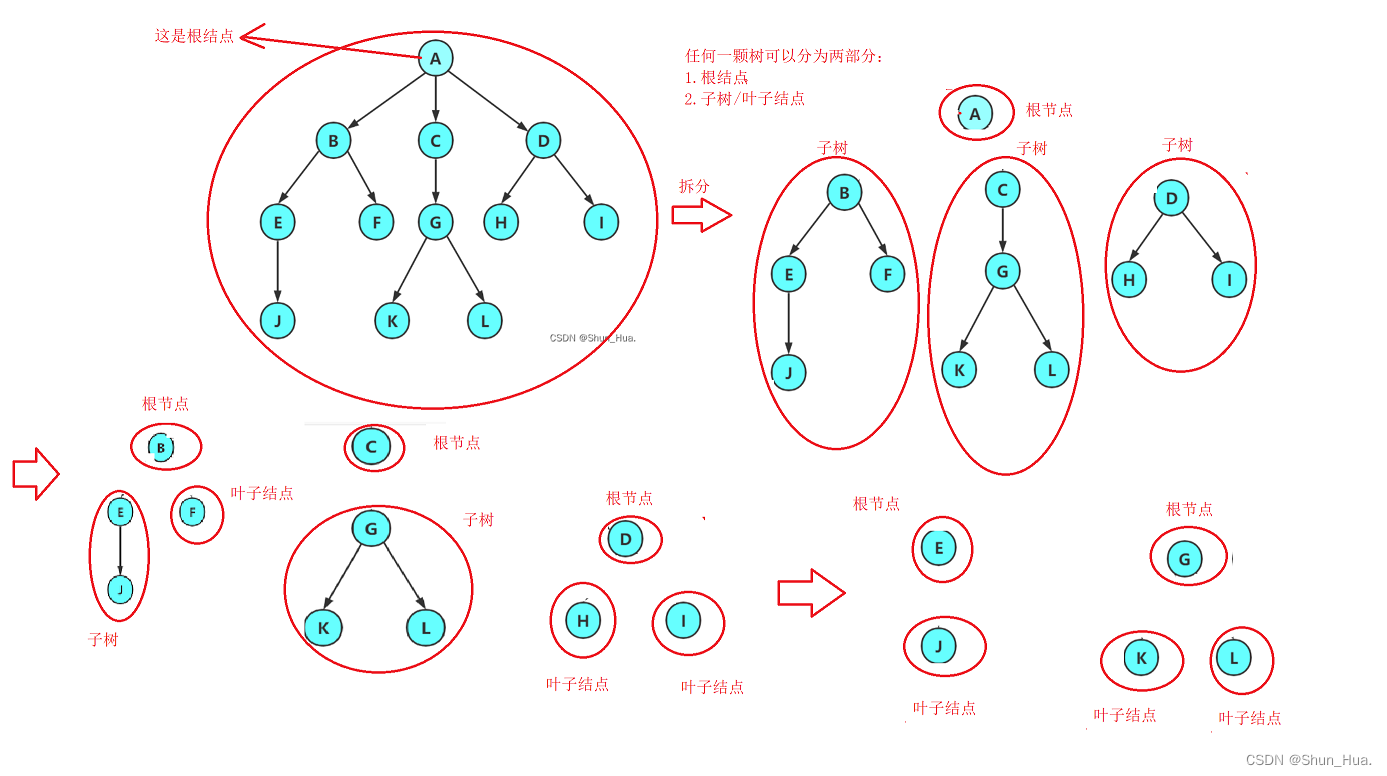
我们接着分析:树是分叉的(从上往下看),也就是说树是分层的,并且层之间的结点,是互不关联的!也就是说树往下分析是一对多的,并且是从上面的唯一 一个节点,分支而来。
例:
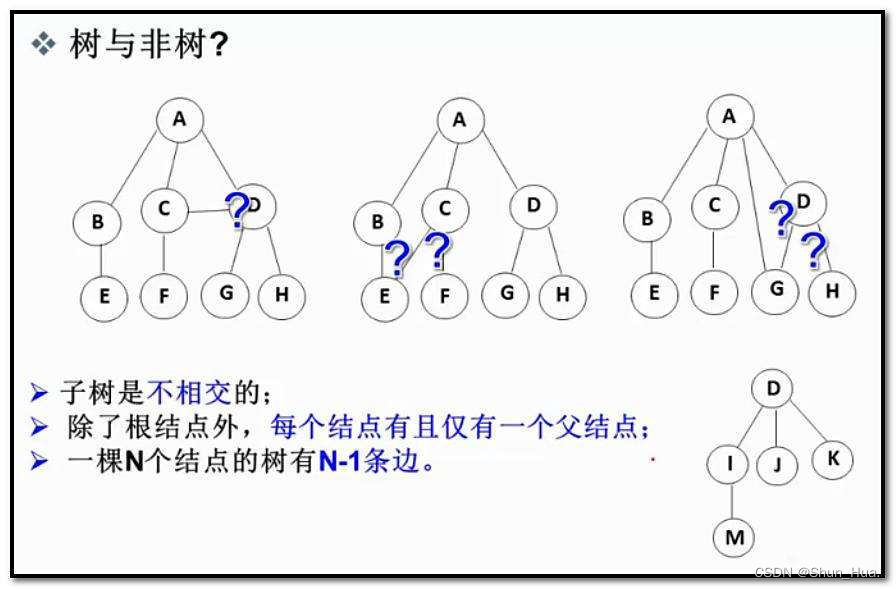
分析:
第一棵树:第二层(从上往下数)C与D之间相关,所以不是树。
第二棵树:第三层 E的节点的上层结点有两个(B和C),呈现多对一(下往上),所以不是树。
第三棵树:第三层G节点从下往上看(有A和D两个节点)呈现多对一的结构,所以不是树。
总结:
树的定义满足:
1.节点数大于等于0
2.满足非线性结构
3.子树是相互独立的,不能交叉。
4.树是可以递归的:
1.根节点
2.子树(只有一个节点也算是子树)
说明:只有一个节点不能再继续分,即递归停止。
树的相关概念:
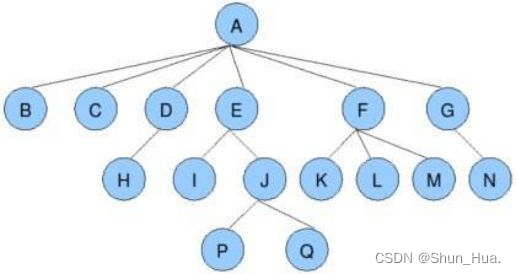
1.节点的度:结点所含的子树的个数称为度。
例:A节点有以B,C,D,E,F,G根节点的树,子树有6个,因此度为6。
二级结论:
证明:
设树最大的度为M,节点个数为N,树的边数为N-1,(2个结点由一个边连起来,由此可推N个结点可由N-1个边数连起来),度为1的结点的边有1条,
度为2的结点的边有2条,可以推出度为N的结点有N条。
设度为0的结点为N0,度为1的结点为N1,度为2的结点为N2……度M的结点为Nm
因此总边数:N-1=0*N0+1 *N1+2*N2+……+M *Nm 。
2.叶节点或终端节点:度为0的节点称为叶节点.
比如:B,C,H,I,K,L,M,N,P,Q结点没有子树,因此是叶节点。
3.非终端节点或分支节点:度不为0的节点
比如:A,D,E,F,G,J,这些结点向下有分支的结点,称之为分支节点。
4.双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点。
5.孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;
比如:A结点向下有分结点——B,C,D,E,F,G。则A称为B,C,D,E,F,G的父节点,那B,C,D,E,F,G就称之为A的子结点(孩子结点)。
6.兄弟节点:具有相同父节点的节点互称为兄弟节点;
A的子结点有B,C,D,E,F,G。A的子结点都有一个父节点,所以B,C,D,E,F,G互称为兄弟节点。
7.树的度:一棵树中,最大的节点的度称为树的度,这里的最大的节点指的是,树中,度为最大的节点。
此棵树中度最大的节点为A,所以A的度就是树的度——6
8.节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推。
比如:A的节点的层数为1,B,C,D,E,F,G的节点的层数为2,H,I,J,K,L,M,N.
节点的层数为3,P,Q的层数为4.
9.树的高度或深度:树中节点的最大层次
从上往下数分了几层就是树的高度,这棵树分了4层,高度就是4。
10.堂兄弟节点:双亲节点在同一层的节点互为堂兄弟,这里的双亲是不同一个父节点。
比如第三层的H,I节点不一个父节点,所以它们互为堂兄弟。
11.节点的祖先:从根到该节点所经分支上的所有节点
比如:Q节点,到达Q节点的路径上的节点,A,E,j这三个节点称之为Q节点的祖先。
12.子孙:以某节点为根的子树中任一节点都称为该节点的子孙。
比如:A是这棵树的根节点,一切节点都由A节点发展而来,所以A是所有节点的祖先,反之,A以下的所有节点称之为A节点的子孙。
13.森林:由m(m>0)棵互不相交的树的集合称为森林。
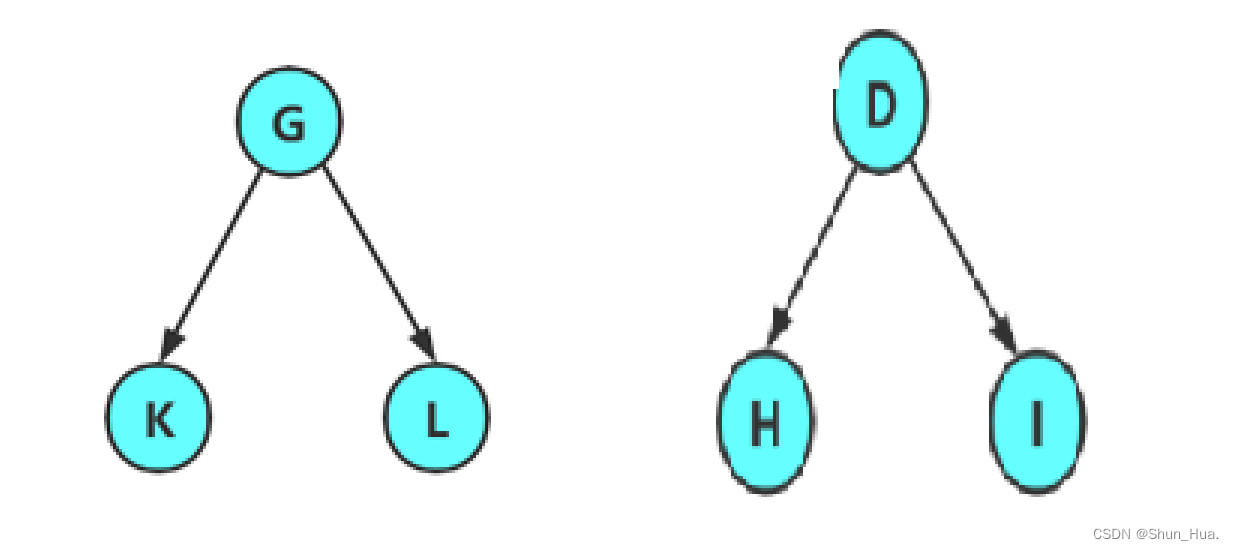
这样的不相交的两棵树称为森林。
一棵树去掉根节点可以变成森林 ,上面的树(最上面那棵大树)去掉A节点,就变成了森林。
二.树的表示方法
如何表示棵树?
由于非线性结构一对多的关系,想表示一棵树很难,由于大佬的存在,有了如下三种表示形式。
1.双亲表示法
由于每个节点都只有一个父节点,所以我们可通过双亲来表示一棵树。具体方式通过数组的形式实现。
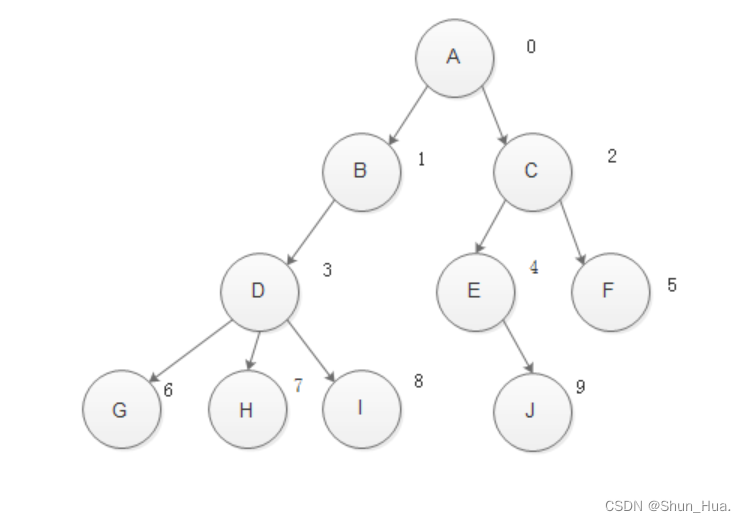
从根节点以下标0的位置(数组的第一个元素下标为0)开始,从左往右依次增大,从上往下呈现增大趋势。
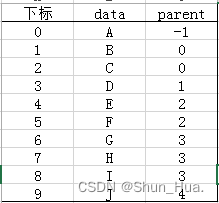
一个数据有两种性质,所存数据的值,父节点的下标位置——根节点没有父节点所以设置父节点的下标位置为-1,因此我们可采用二维数组的形式进行存储信息(父节点存的是元素的行标,元素的下标恒为0)。
2.孩子表示法
由于每个节点都可能有孩子,所以我们通过数组的形式,数组的元素为链表(用于记录该节点的孩子),从而表示一棵树。
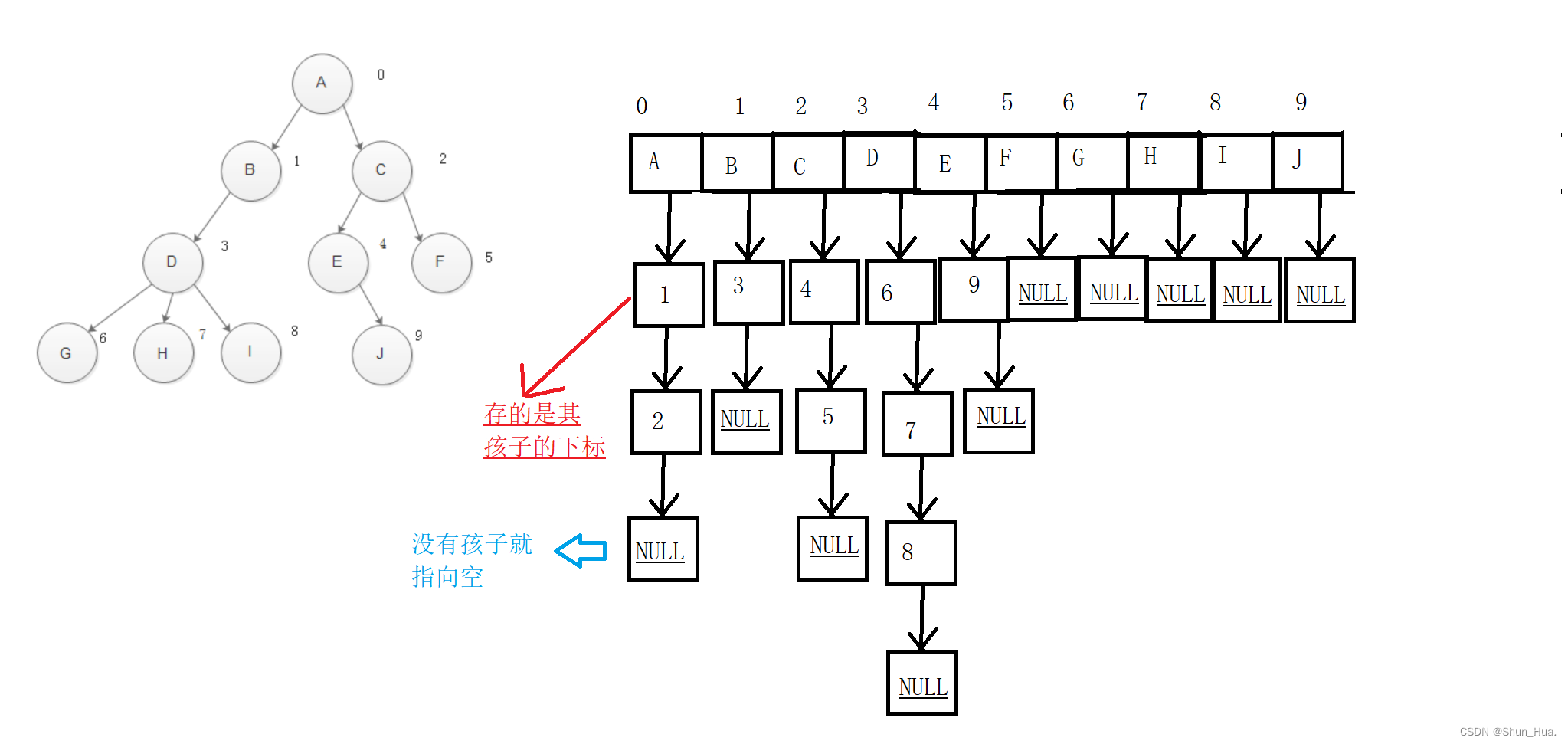
3.孩子兄弟表示法
每个节点都可能有亲兄弟和孩子结点,所以我们可以通过链表的形式,进行表示。
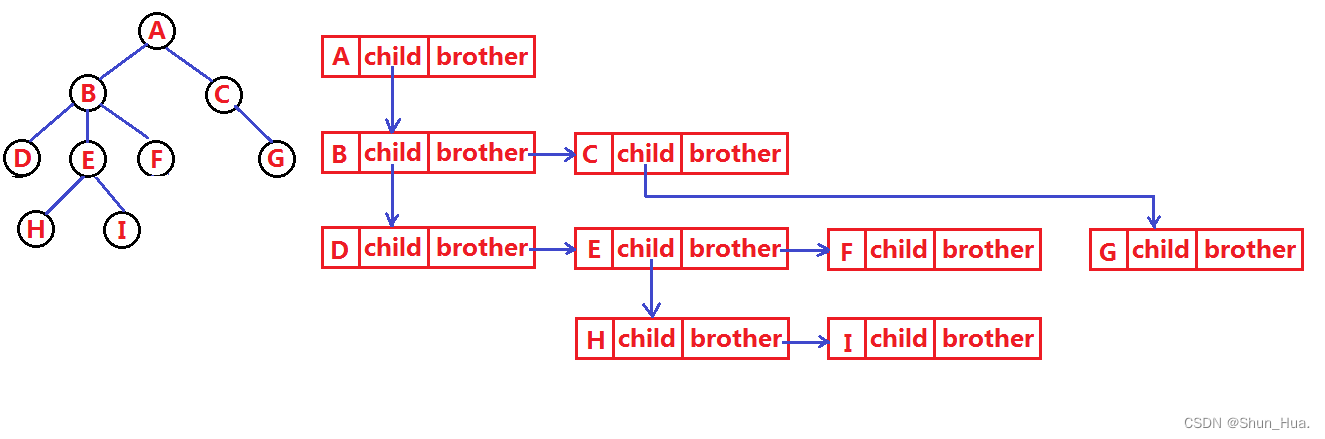
这样父节点可以间接地指向其所有的孩子。
三.二叉树
1.概念
1.二叉树是指树中节点的度不大于2的有序树,它是一种最简单且最重要的树。
递归定义:
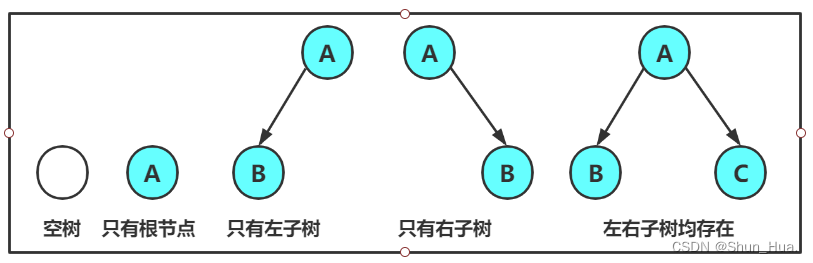
二叉树是一棵空树,或者是一棵由一个根节点和两棵互不相交的,分别称作根的左子树和右子树组成的非空树;左子树和右子树又同样都是二叉树,这跟树的递归很像。
图:

特点:
1. 二叉树不存在度大于2的结点
2. 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
说明: 这里的不能颠倒指的是:颠倒之后就不是原来的树了,所以树有左右之分,并且树是有序的。3.任何一棵二叉树都由以下几个组成部分组成:
2.特殊的二叉树
满二叉树
定义:每一层的结点都满了不能再插入结点。
图:
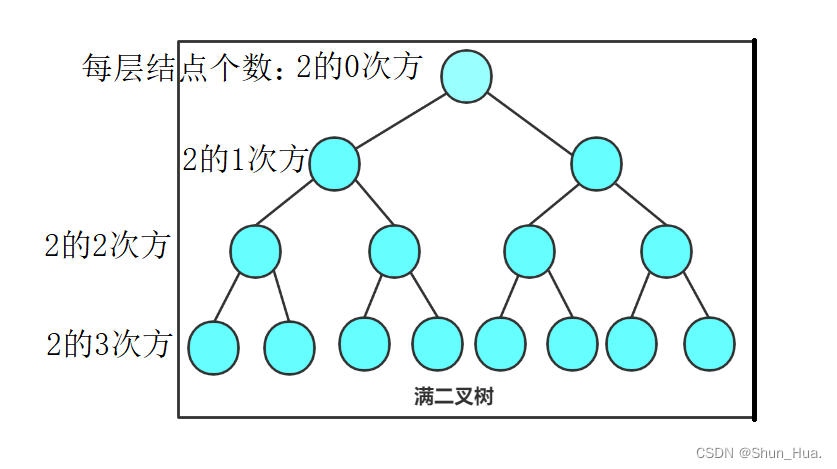
结点的个数:设高度/深度为h
T(N)=2^0 + 2的1次方+2的2次方+……2的h-1次方,由等比数列前N项和可得
T(N)=2的h次方-1
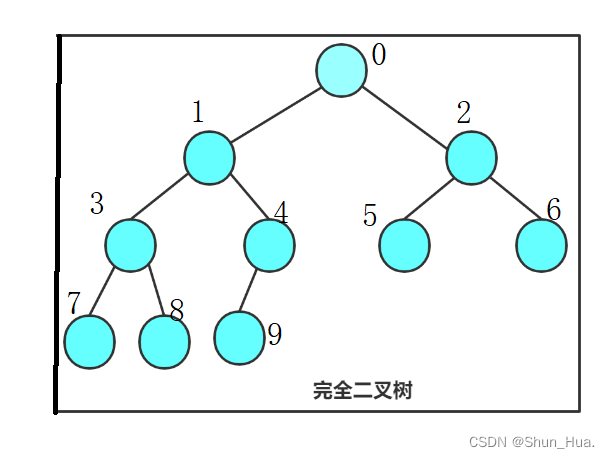
完全二叉树
定义:设完全的二叉树的高度为h,则h-1层的结点满了,h层的结点至少为1个。
图:
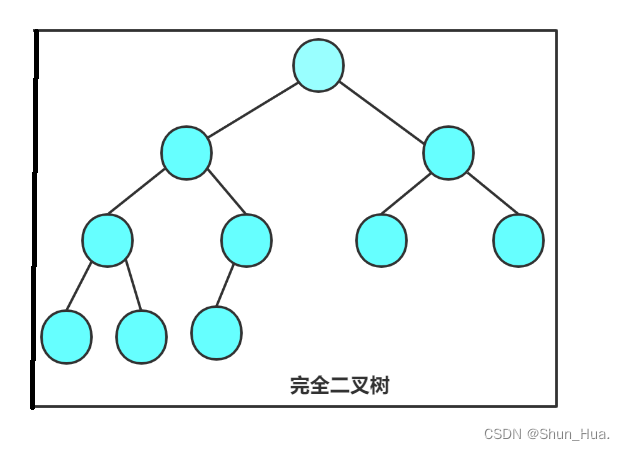
结点个数的范围:设高度为h
完全二叉树的特殊情况:最后一层只有1个节点,或满二叉树。
最后一层只有1个节点:T(N)=2的h减一次方-1(这是前h-1层满的情况)+1(最后一层为1)
满二叉树: T(N)= 2的h次方-1
因此节点的范围:2的h减1次方到2的n次方减一,这是闭区间。
注意:
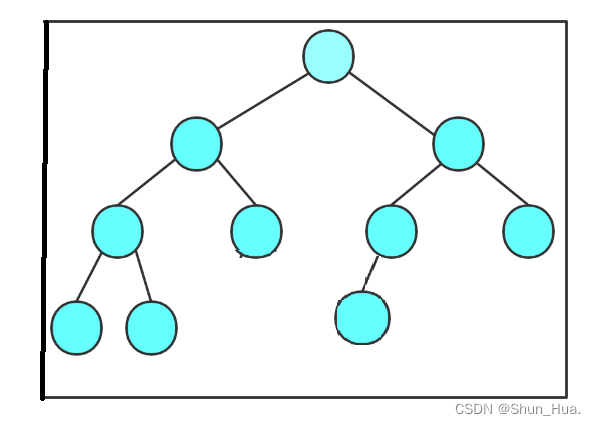
这种的 最后一层的节点没有按顺序排列不叫完全二叉树。
二叉树结论
设高度为:h,二叉树的节点个数为N
1.分空二叉树的最多节点数:2的h次方-1
2.最深层的最多节点数:2的h减一次方
3.满二叉树的节点数:2的h次方-1
4.完全二叉树的节点数范围:2的h-1次方到2的h次方-1
5.满二叉树的深度为:log以2为底(N+1)
6.完全二叉树的最小深度:logN + 1,对数的底数为2
7.一个结点的孩子结点为:2M+1,2M+2,(M是结点的下标)
代入下图验证一下