典型相关分析python实现

典型相关分析概念以及流程

典型相关分析由Hotelling提出，其基本思想和主成分分析（PCA）非常相似。首先在每组变量中找出变量的线性组合，使得两组的线性组合之间具有最大的相关系数；

线性组合如图所示，即综合了各种变量，例子中和为其中一种线性组合，一般线性组合不止有一个，一般为变化后的特殊矩阵特征值的个数。

假设原来两组变量如下

通过提取线性组合，直至将相关性被提取完毕，而且被选出来的线性组合被称为典型变量，而且典型变量的相关系数成为典型相关系数，典型相关系数代表了两组变量之间的联系强度。这也就是我们常说的典型相关分析，如果用spss的话还会有典型负载分析，通过这个我们可以得知哪个线性组合对于方差的贡献最大（最显著）

典型相关系数求解简介

1. 选取和最初挑选的这对线性组合不相关的线性组合，使其配对，并选取相关系数最大的一对线性组合；这里的相关系数一般为Pearson相关系数。而且要保证线性组合的协方差为0。如下所示。

（目的是保证线性组合不相关，以便于提取不一样的信息）

此外，要保证方差相同且为1，（消除量纲的影响，相关系数与量纲无关）。

2. 重复之前的步骤，直到两组变量之间的相关性被提取完毕为止。被选出的一对线性组合称为典型变量，（个数一般不超过最后求解的协方差矩阵的特征向量的个数）它们的相关系数称为典型相关系数。一般用假设检验去证明显著性。典型相关系数度量了这两组变量之间联系的强度。

典型相关系数完整代码

# 参考：https://blog.csdn.net/wyn1564464568/article/details/125966449
# 参考：https://blog.csdn.net/Python_xiaowu/article/details/122258245
from math import sqrt
import numpy as np
import pandas as pd

from utils.basic_operation import read_csv_float
# x_data，y_data为行向量，
'''
    x_data的大小为一个（特征数量*样本数）的一个矩阵，
    y_data的大小为一个（特征数量*样本数）的一个矩阵
'''
def calculate_CCA(x_data,y_data):
    # 将x_data，y_data转换为float64的类型的数据
    x_data = np.array(x_data, dtype='float64').T
    y_data = np.array(y_data, dtype='float64').T
    '''
    rho:典型变量的相关系数
    alpha:自变量系数
    beta:因变量系数
    '''
    # A放置的是将要标准化的矩阵，而且是是两组系数之间的整合
    temp_matrix = []
    for sample in x_data:
        temp_matrix.append(list(sample))
    for sample in y_data:
        temp_matrix.append(list(sample))
    temp_matrix = np.array(temp_matrix, dtype='float64')
    # temp_matrix这一步是讲两个矩阵组合成一个矩阵组合在一起
    # 标准化：减去每行的均值再除以标准差
    for i in range(0, temp_matrix.shape[0]):
        avg = np.mean(temp_matrix[i])
        std = np.std(temp_matrix[i])
        temp_matrix[i] = (temp_matrix[i] - avg) / std
    # bias = True 即为计算的时候不采用对方差的无篇修正（除以n-1，样本方差）
    cov_matrix = np.cov(temp_matrix, bias=True)
    print(cov_matrix.shape) # 协方差矩阵为两个变量组合起来的特征数量，而且为为方阵。这里这个矩阵还为相关系数矩阵
    n = x_data.shape[0] # n为变量数量，而且y_data和x_data的样本数量一致
    R_11 = np.matrix(cov_matrix[:n, :n])
    R_12 = np.matrix(cov_matrix[:n, n:])
    R_21 = np.matrix(cov_matrix[n:, :n])
    R_22 = np.matrix(cov_matrix[n:, n:])
    # linalg.inv计算矩阵的逆
    M = np.linalg.inv(R_11) * R_12 * np.linalg.inv(R_22) * R_21
    N = np.linalg.inv(R_22) * R_21 * np.linalg.inv(R_11) * R_12
    eig_value, eig_vector = np.linalg.eig(M)
    data = []
    # 典型相关系数的格式为矩阵的特征值的数量
    for i in range(0, len(eig_value)):
        # 精度偏差
        if abs(eig_value[i]) < 1e-7:
            continue
        # 上面的步骤和下面的一致，都是向下取整，即为取到几位小数
        # rho为典型相关系数，alpha为自变量系数，beta为因变量系数
        rho = np.round(sqrt(eig_value[i]).real, decimals=5) # decimals为确定的精度系数
        alpha = np.round(eig_vector[:, i],decimals=5)
        k = 1 / (alpha.T * R_11 * alpha).real
        alpha *= sqrt(k)
        beta = np.round(np.linalg.inv(R_22) * R_21 * alpha / rho, decimals=5)
        data.append((rho, alpha, beta))
    # 进行排序处理，即为做到归一化处理，这里是根据key=function函数进行排序，而且reverse=True的时候为降序排序
    data.sort(key=lambda  x: x[0], reverse=True)
    return data
if __name__=="__main__":
    x_data = []
    y_data = []
    data = pd.read_excel("health.xlsx")
    for i in range(0, len(data.columns)-3):
        x_data = data.iloc[:,[0, 1, 2]]
        y_data = data.iloc[:,[3, 4, 5]]
    names = data.columns
    # print(np.array(x_data))
    # print(np.array(y_data))
    # x_data = [[191, 36, 50], [189, 37, 52], [193, 38, 58]]
    # y_data = [[5, 162, 60],[2, 110, 60], [12, 101, 101]]
    res = calculate_CCA(x_data, y_data)
    print(calculate_CCA(x_data, y_data))

求解典型相关系数具体流程

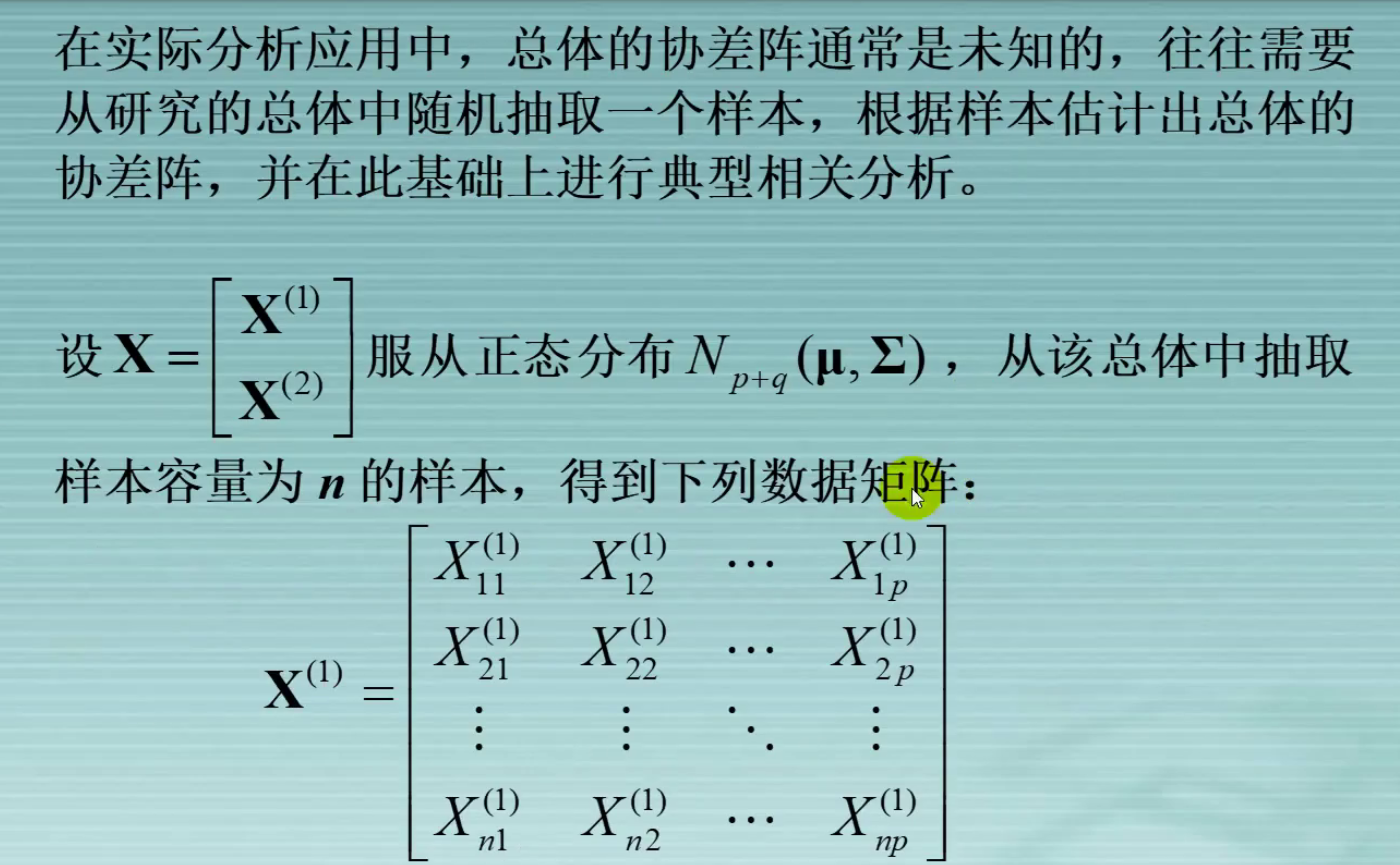
1. 检验两组数据是否符合联合正态分布，两组变量分别为，而且这两个分别为之前提及的矩阵，最后获得的矩阵大小为（样本个数*变量数量）的矩阵。

2. 标准化协方差矩阵，消除了量纲的影响，标准化后的协方差矩阵为相关系数矩阵。之后利用标准化典型变量进行典型分析。

求典型变量（特征向量）和典型相关系数（特征值）

代码如下，这一步为求解的关键，即为推导过程也许我们不一定能看懂，在这里就省略一部分。

    R_11 = np.matrix(cov_matrix[:n, :n])
    R_12 = np.matrix(cov_matrix[:n, n:])
    R_21 = np.matrix(cov_matrix[n:, :n])
    R_22 = np.matrix(cov_matrix[n:, n:])
    # linalg.inv计算矩阵的逆
    M = np.linalg.inv(R_11) * R_12 * np.linalg.inv(R_22) * R_21
    N = np.linalg.inv(R_22) * R_21 * np.linalg.inv(R_11) * R_12
    eig_value, eig_vector = np.linalg.eig(M)
    data = []
    # 典型相关系数的格式为矩阵的特征值的数量
    for i in range(0, len(eig_value)):
        # 精度偏差
        if abs(eig_value[i]) < 1e-7:
            continue
        # 上面的步骤和下面的一致，都是向下取整，即为取到几位小数
        # rho为典型相关系数，alpha为自变量系数，beta为因变量系数
        rho = np.round(sqrt(eig_value[i]).real, decimals=5) # decimals为确定的精度系数
        alpha = np.round(eig_vector[:, i],decimals=5)
        k = 1 / (alpha.T * R_11 * alpha).real
        alpha *= sqrt(k)
        beta = np.round(np.linalg.inv(R_22) * R_21 * alpha / rho, decimals=5)
        data.append((rho, alpha, beta))

1. 对变量进行相关性检验（构造的统计量为似然比统计量），目的是去检验协方差矩阵是否为0。

   扫描二维码关注公众号，回复： 14664367 查看本文章

假设和似然比统计量如图所示。

2. 确定典型相关系数的个数，这里运用的是Bartlett检验，检验假设和检验所需要的统计量如下图。

3. 进行典型载荷分析正负相关性

4. 计算典型变量对于样本总方差的贡献，在这里我们可以理解为将前面获得的线性组合系数进行逐个平方相加之后除以线性组合个数，最后获得的就是第i组典型相关系数对于应变量的贡献程度。